This paper introduces a newly recognized process in which electrons can briefly pair up at close range based upon a balance of forces between electrical repulsion (i.e., charge) and magnetic attraction (i.e., spin) in a manner wholly distinct from the electron pairing process explained in traditional theories of superconductivity. The resultant twoelectron state is a short-lived Compton-scale composite where the two electrons are held together in a balance of opposing forces.

Keywords: Superconductivity; Electrons; Plasmas.

Background and Introduction

Over the past few decades, the search for higher-temperature superconducting materials has resulted in a number of interesting candidates. Yet, it has been difficult to understand the behavior of these materials within the now-standard picture of the Bardeen, Cooper, Schrieffer (BCS) theory of superconductivity [1]. As a result, these new materials have been referred to as unconventional superconductors. Norman [2] reviewed the status of the unconventional superconductors and noted that they represent a substantial “challenge” to understanding how they work either within, or outside of, the BCS framework.

An important characteristic of the BCS theory made use of “Cooper pairs” previously introduced by L. Cooper [3]. Cooperʼs electron pairs, while very different from the tandem-electron pairs described in this paper, represent one impetus for this work. A second impetus comes from the late Turkish-American physicist Asim O. Barutʼs observation that it was strange that most of our well-studied physical composites, e.g., atoms, result from electrostatic interactions at large distances while neglecting magnetic interactions at short distances. In contrast, this paper considers both interactions on an equal footing resulting in the possibility that electrons can briefly pair up in a balance of forces between electrical repulsion and spin-mediated magnetic attraction. The implications of such a “tandem-electron pair” (as I refer to them here) even if short-lived, could be potentially significant and will be considered near the end of this paper.

Tandem electrons

Basic electrostatics suggests that electrons could not pair up because they would be repelled by their respective negative charges. However, under special conditions, when electrons come into proper alignment, their magnetic attraction can become strong enough to pull them together tightly in a short-lived, “quasi-bound” state in which the electrical forces of repulsion are perfectly balanced by the magnetic forces of attraction (see Figure 1 below). It is important to note the very small size of these pairs (on the Compton scale) as compared to atoms.

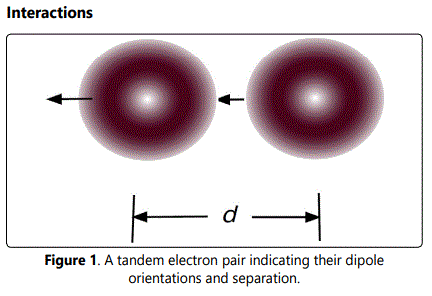
There are two types of interactions of tandem electrons oriented as shown in Figure 1. The first is the magnetic dipoledipole interaction, well-studied when the dipoles are of macroscopic scale. The second is the electrostatic charge interaction of the two electrons. The magnetic dipole-dipole interaction is attractive just as in the macroscopic case of two bar magnets. The electrostatic interaction, on the other hand, is repulsive, thus presenting the possibility of a balance of forces.

Letʼs examine the magnetic dipole-dipole interaction first. The form of this interaction may be found in, for example Scott [4]. The potential can be written

where the mʼs are the dipole moments. In this case,

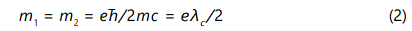
where λ_c is the electron Compton wavelength. This gives

But there is also the electrostatic repulsion between the electrons,

So the full-potential can be written

Now, measuring d in terms of λ_c, i.e., z = d/λ_c, U^′_full can be written as,

where E_c = e²/λ_c ≈ 3.7 keV.

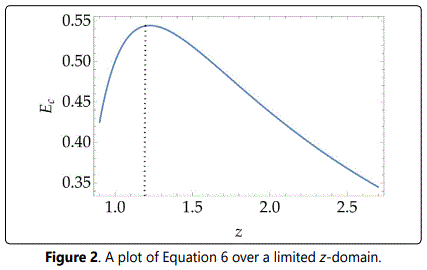
Figure 2 is a plot of Equation. 6 indicating a peak located at z = 1.22 having a value E_c = 0.54 or about 2 keV. Note here it is unlikely that the zone inside of the peak is accessible for pair formation due to wave-function overlap. However, near the peak, the balance of the magnetic and electric forces appears to provide a robust (with respect to collisions) connection between the electrons. In general however, there will be many electrons that remain unpaired. It is interesting that even though the magnetic dipole-dipole force falls off rapidly between the electrons, they are nonetheless accelerated toward each other to form a “pair” so long as the spins remain similarly aligned. This means that, while such pairs may be small in number under most conditions, they are still likely present. In other words, although the conditions necessary to enable electron pairing make them uncommon, their existence appears not only theoretically possible, but quite likely.

Tandem Electrons as basic “compton composites”

Tandem electrons represent a Compton-scale composite system without a positive nuclear core (e.g., a proton, deuteron, etc.) which was the focus of our paper that first introduced “Compton composites” [5a]. This suggests that tandem electrons are a “scattering resonance” and thus remain connected only briefly because they are not a bound state.

A straightforward estimate for the tandem electronʼs lifetime can be calculated according to the energy-time form of the Heisenberg uncertainty relation as

Note that this is a very short time for tandem electrons to exist together after which they return to the population from which they came. However, it is interesting to consider the possibility that these brief electron pairings could themselves become part of another composite particle. These additional composites, as explained below, could have broader implications.

Broader implications

As stated above, this paper was initially motivated by the problems in unconventional superconductors in which tandem electrons may or may not play a role but the basic nature of tandem electrons appears to have broader implications.

Although the balance of forces calculation for tandem electrons shown above is instructive, it is a “classical” one and is therefore unlikely to be a final answer. Clearly, a fully quantum mechanical solution must be examined for electron pairing, a difficult problem probably requiring a QED calculation. Hopefully, such a calculation may be presented in the near future.

Tandem electrons appear to be a somewhat more general “pairing” than are “Cooper pairs” because interactions with an atomic lattice are not necessary for their formation. Therefore, this pairing might occur in more diverse physical situations. In other words, the balance of forces that give rise to tandem electrons is likely to occur under a wider variety of situations, e.g., (i) in certain metals with large free-electron populations, and (ii) in some materials where the atomic electrons can come into near contact (especially under pressure) at the small distances required, and finally (iii) in plasmas.

If tandem electron pairs form and if they can form in a wider variety of circumstances than \Cooper pairs,” there could be some signicant and interesting implications, even if these pairs come together only briey. For example, during the brief lifetime of a tandem electron pair, it might encounter a free proton whose positive charge could allow it to bind with the negatively charged electron pair, resulting in another Compton-scale composite. My late colleague John Reitz and I discovered this possibility and referred to this \secondary” composite as a tresino since it is composed of three particles: two electrons (the tandem electron pair) and a proton [5,6]. Whatʼs most interesting about this composite is that its formation results in the release of binding energy (≈ 3:7 keV) and itʼs stable and long-lived compared to the tandem-electron pair, because it is a bound state.

It seems likely that in many situations in which a mysterious release of energy is observed in solids or plasmas, will have started by first forming a transient tandem electron pair, but then through a collision with a proton, became a bound-state Compton composite thereby releasing its binding energy. An example of this type of tresino formation, namely the possibility of a negatively-charged tandem electron pair colliding with a free proton might have been crucial in the Early Universe [7].

Many implications of bound state Compton composites have been examined in our papers over the past few years. Perhaps more will be examined now given the broadened scope of tandem electron pairs as basic Compton composites.

Conclusions

An alternate method by which electrons can pair-up has been presented. It is not clear that this pairing will be helpful in understanding the unconventional superconductors. But, on the other hand, tandem electron pairs have been recognized as a basic Compton-scale composite that could be important in the broader understanding of other such composites.

Dedication

I dedicate this paper to my late friend and collaborator, John R. Reitz, without whose efforts this work would not have been possible, and to the late Asim O. Barut, who foresaw the importance of magnetic interactions at short distances.

References

1. Bardeen J, Cooper LN, Schrieffer JR. Theory of Superconductivity. Phys Rev. 1957; 108: 1175-1204.   
2. Michael R. Norman. Science. 2011; 332(6026): 196-200.   
3. Cooper LN. Bound electron pairs in a degenerate fermi gas. Phys Rev. 1956; 104(4): 1189-1190. doi: 10.1103/PhysRev.104.1189   
4. Scott WT. The Physics of Electricity and Magnetism. John Wiley & Sons, Inc. 1950; 373-375.   
5a. Mayer FJ, Reitz JR. Electromagnetic Composites at the Compton Scale. Int J Theor Phys. 2012; 51: 322-330. doi: 10.1007/s10773-011-0959-8   
5. Mayer FJ. Hidden Baryons: the Physics of Compton Composites. EPL. 2016; 114(6): 69001. doi: 10.1209/0295- 5075/114/69001.   
6. Mayer FJ, Reitz JR. Corrigendum to Thermal energy generation in the earth. Nonlin Processes in Geophys. 2014; 21(2): 367-378. doi: 10.5194/npg-21-503-2014   
7. Mayer FJ, Reitz JR. Compton Composites Late in the Early Universe. Galaxies. 2014; 2(3): 382-409. doi: 10.3390/galaxies2030382