Abstract

Here, we investigate cosmological models with perfect fluid source in the framework of Kaluza- Klein FRW space time in a modified theory of gravity known as f (R, T) gravity (Harko et al. 2011) where R is the Ricci scalar and T is the trace of the stress energy tensor of the perfect fluid. By solving the field equations, we have found an exact solution of the field equations using a linearly varying deceleration parameter which can be considered as a five dimensional FRW type cosmological model in f (R, T) gravity. We have determined the spatial volume and average Hubble parameter of the model. We have also determined and discussed the physical parameters, pressure and density for dust, radiation and stiff matter dominated eras.

Keywords: Kaluza-Klein model; FRW models; Cosmological models; Perfect fluid; f (R, T) gravity.

Introduction

It s well known that Einstein’s theory of gravity has been successful in describing the gravitational phenomena and cosmology and cosmological models of the universe. However, it is said that this theory does not fully account for certain aspects of present day cosmology. To mention some of them, we can say that Einstein’s theory does not fully incorporate famous Mach’s principle, it does not avoid singularity problem and does not explain the modern scenario of accelerated expansion of the universe. Riess et al. [1] and Perlmutter et al. [2] have confirmed that the universe is not only expanding but it is accelerating by analyzing their Supernova 1a experimental data. It is also proposed that a huge negative pressure known as dark energy is responsible for this cosmic acceleration. In order to explain this two approaches have been proposed. One way is to investigate several dark energy candidates [3-7] and another way is to modify Einstein’s theory of gravitation. Hence modifying Hilbert-Einstein action some modified theories of gravitation have been formulated. Significant among them are f (R) gravity [8], f (R, T) gravity [9] and scalar-tensor theories of gravitation constructed by Brans-Dicke [10] and Saez and Ballester [11]. Here we are interested in f (R, T) gravity.

A modified theory of gravity known as f (R, T) gravity has been formulated by Harko et al. [9], using the action

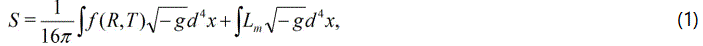
have obtained the gravitational field equations of the theory. Here the gravitational Lagrangian L_m is given by an arbitrary function of Ricci scalar R and of the trace T of the energy momentum tensor T_ij. Generally, the gravitational field equations depend on nature of the matter source. The gravitational field equations of f (R, T) gravity are obtained by varying the action given by Eq. (1) with respect to the metric g_ij (the detailed derivation is found in Harko et al. [9]) as

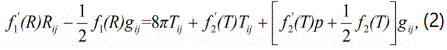
Here prime indicates the derivative with respect to the argument, the function f (R, T) is taken as

where f (T) is an arbitrary function of the trace of the stress energy tensor given by

ρ and p being the density and isotropic pressure, respectively of the fluid, u_i is the four velocity of the comic fluid and the other symbols in Eq. (2) have their usual meaning. Also, Harko et al. [9] presented the field equations of several particular models corresponding to some other explicit forms of the function f (R, T) .

Several interesting cosmological models have been investigated in f (R, T) theory of gravitation by choosing appropriate function f (T) . Harko et al. [9] discussed FRW cosmological models. They have also discussed the case of scalar fields and Brans-Dicke (BD) type formulation of the model which play an important role in cosmology. Many authors have investigated perfect fluid cosmological models in this particular theory. Adhav [12] discussed Bianchi type-I perfect fluid model in f (R, T) gravity while Chandel and Shri Ram [13] and Reddy et al. [14] have investigated several aspects of Bianchi type-III perfect fluid cosmological models in this theory. Sharif and Zubair [15] have obtained anisotropic universe models with perfect fluid and scalar field in this particular theory of gravity. Rao and Neelima [16] discussed perfect fluid Einstein-Rosen universe in this theory while Kaluza-Klein perfect fluid models in this theory are given by Reddy et al. [17]. Mishra et al. [18] have studied non-static cosmological model in this theory of gravity. Aditya et al. [19] obtained Bianchi type-I, VIII and IX perfect fluid models in f (R, T) gravity. Also, Rao et al. [20] have considered Bianchi type-VI_h perfect fluid model in this theory. Santhi et al. [21] have investigated Kantowski-Sachs scalar field cosmological models in f (R, T) gravity. Ramesh and Umadevi [22] have discussed FRW cosmological model in the presence of perfect fluid in this theory. Higher dimensional spherically symmetric models of the universe filled with perfect fluid source in f (R, T) gravity have been studied by Samanta and Dhal [23]. The theory of Kaluza-Klein (KK) [24, 25] is the result of an attempt to formulate five dimensional general relativity in which extra dimensions is used to couple the gravity and electromagnetism. An excellent review of this theory has been presented by many authors [26-28]. Darabi [29] in an interesting paper, tudied the non-compact, non-Ricci KK theory and has shown that the field equations with suitable equation of state (EoS) describe the early inflation and late time acceleration. Santhi et al. [30, 31] have studied KK cosmological models with two fluids source in Brans-Dicke and Saez-Ballester scalar-tensor theories of gravitation. Jamil and Debnath [32], Pradhan et al. [33], Ozel et al. [34] and Sharif and Farida [35] discussed FRW type KK cosmology in general relativity.

The present work is motivated by the above discussion. Here we consider non-Ricci, non-compact FRW type KK cosmological model in the presence of perfect fluid source in the framework of f (R, T) gravity. We organize the paper as follows: in Sect. 2, the field equations and the KK model are presented.Sect. 3, is devoted to the discussion of the behavior of cosmological parameters of the model. Summary and conclusions are given in Sect. 4.

f (R, T) gravity field equations and KK models

The geometry of FRW type KK cosmology is defined by the following metric [33, 34]

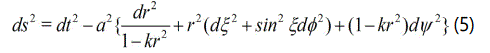
where a(t) is the scale factor of the universe, k= -1, 0, +1 is the curvature parameter for open, flat, closed models respectively. We assume the 5D energy momentum tensor for perfect fluid as

here the five velocity vector ui satisfies u_iuⁱ =1.

Now, using comoving coordinates and [9]

we can write down the field equations of f (R, T) gravity given by Eq. (2) with the help of Eq. (6) for the metric (5) as

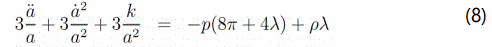
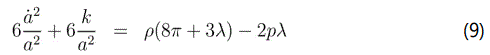
where an overhead dot denotes differentiation with respect to cosmic time t. The above system consists of two equations but three unknowns (a(t), ρ and p), hence is not fully determined. One may determine the system fully by specifying a theory that determines a relation between the energy density and pressure of the fluid. Most of the perfect fluids relevant to cosmology obey an equation of state of the form

where ω is the equation of state (EoS) parameter, not necessarily constant. It may be noted that when ω is constant we obtain the well known cosmological fluid models-dust model (ω = 0), stiff fluid model (ω = 1), radiating model (ω = 1/3) and false vacuum or vacuum energy model (ω = -1). In literature, it is well known, that several authors have obtained perfect fluid models by solving the field equations of general relativity and modified theories of gravitation using the law of variation for Hubble’s parameter proposed by Berman [36] and Berman and Gomide [37] which yields constant deceleration parameter models

where m ≥ 0 is a constant. Here we solve the field equations (8) and (9) using linearly varying deceleration parameter (LVDP) proposed by Akarsu and Dereli [38] given by

where k ≥ 0 and m ≥ 0 are constants and k = 0 reduces Eq. (12) to the Hubbleʼs law of Berman [36] which yields constant deceleration parameter models of the universe. Ramesh and Umadevi [22] have investigated FRW cosmological models with LVDP in f (R, T) gravity. Sarkar [39] have obtained Bianchi type-V holographic dark energy universe with LVDP. Sahoo and Sivakumar [40] have studied LRS Bianchi type-I cosmological model in f (R, T) theory of gravity using this LVDP. Santhi et al. [41] have discussed Bianchi type-III magnetized holographic Ricci dark energy models using LVDP.

Following the discussion presented in [38], we observe that Eq. (12) leads to super exponential expansion unless k = 0. Now, solving Eq. (12) we obtain three different solutions given as

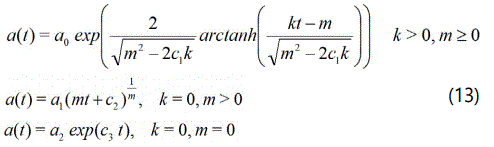
where a₀, a₁, a₂, c₁, c₂, c₃ are constants of integration. It may be noted that the last two of the solutions in Eq. (13) give us the constant deceleration parameter of the models of the universe.

Here we are interested in the perfect fluid model with linearly varying deceleration parameter model which is new. Now, choosing the integration constant c₁ = 0 and m > 0 we obtain

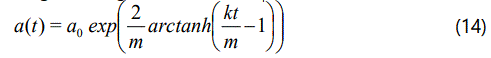
Now, using Eq. (14) in Eq. (5) the FRW type KK model in f (R, T) gravity can be written as

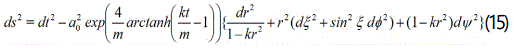
Physical discussion of cosmological parameters

In this section,we determine the cosmological parameters of the model given by Eq. (15) and discuss their physical behavior in cosmology.

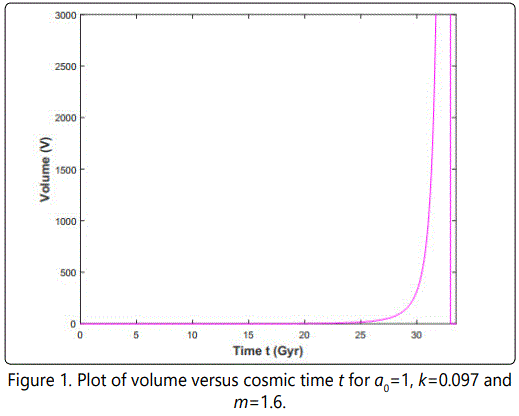
The spatial volume of the model is given by

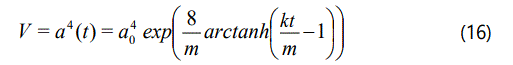
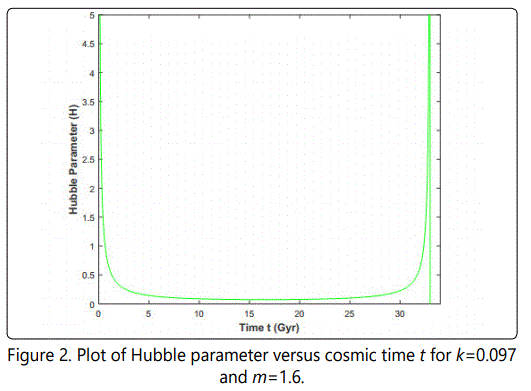
The average Hubble parameter of the model is

Now, since the field equations (8) and (9) are highly non-linear we evaluate the physical parameters pressure and density in the universe (15) for dust, stiff matter and radiation dominated eras by substituting ω = 0,1,1/4 in Eq. (10).

Case-1 (ω=0)

In this case we have from the field equations (8) and (9) the pressure and density as

p = 0

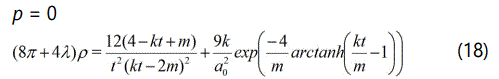
Case-2 (ω = 1)

In this case the pressure and density are given by

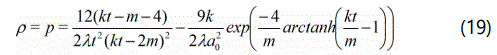
Case-3 (ω = 1/4)

In this particular case we have the pressure and density as

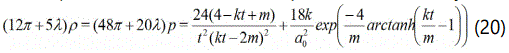
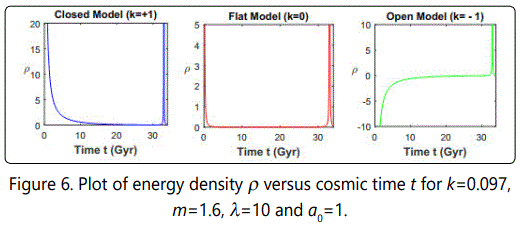
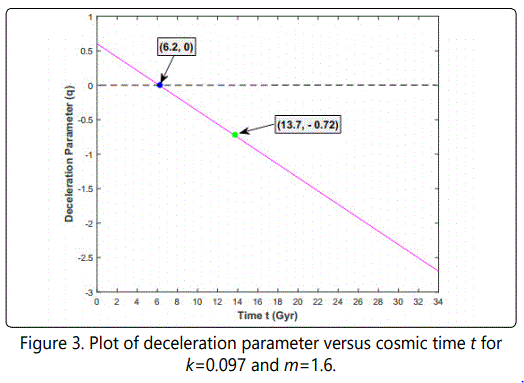
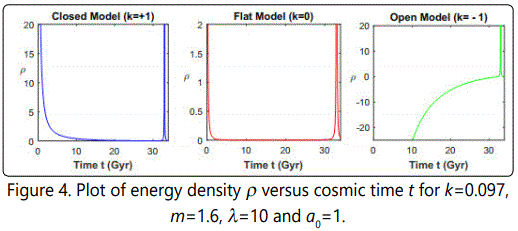
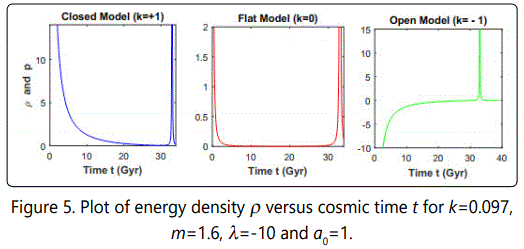
From Figure 1 it may be observed that all the models evolve from zero volume, increase with cosmic time and ends at t_end≈33 Gyr. From observational data we know that the model attains big rip singularity at t_rip≈35 Gyr (Caldwell [42]). It can be seen that our model is close to the given lifetime for the universe. From Figure 2, it is clear that the Hubble parameter H diverges at the beginning and at the end (i.e., at t_end=3 Gyr) of the universe. Figure 3 gives the time varying behavior of the deceleration parameter which exhibits transition of the universe from decelerated phase to the accelerated phase. In fact this happens at t ≈6.2 Gyr and the present (i.e. at t=13.7 Gyr) value of the deceleration parameter is q=-0.72 which confirms the observational results of modern cosmology (Cunha [43]). Figures 4-6 show that the energy density of the fluid, in all the above cases, diverge at the beginning and at the end of the universe. Also, we can observe that our models end with a big rip singularity. We notice from these figures that the open models (k=-1) are not possible because of the fact that the positivity condition of the energy density of the fluid is violated in all the cases.

Conclusions

This paper is devoted to the discussion of non-Ricci, non compact FRW type Kaluza-Klien cosmological models in the presence of perfect fluid source in f (R, T) gravity. The field equations of the theory are solved using a linearly varying deceleration parameter which includes Berman’s law [36] that yields constant deceleration parameter models. We have presented FRW five dimensional cosmological models in f (R, T) gravity. Cosmological parameters corresponding to dust, stiff fluid and radiating models are determined and their physical behavior is studied. It is observed that the spatial volume of the universe starts with a big bang at t=0 and ends with a big rip singularity. The energy densities of all the models diverge both at the beginning and at the end of the universe. The models exhibit a smooth transition from early deceleration to present accelerated phase of the universe. It is observed that the models and their physical behavior confirm the recent cosmological data (Caldwell [42]; Cunha [43]; Akarsu and Dereli [38]).

References

1. Riess A. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant . Astron J. 1998; 116: 1009. doi: 10.1086/300499   
2. Perlmutter S. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys J. 1999; 517: 565. doi: 10.086/307221   
3. Bento M. Generalized Chaplygin gas accelerated expansion, and darkenergy-matter unification. Phys Rev D. 2003. doi: 10.1103/PhysRevD.66.043507   
4. Cohen A. Effective Field Theory Black Holes and the Cosmological Constant. Phys Rev Lett. 1999; 82. doi: 10.1103/PhysRevLett.82.4971   
5. Sheykhi A. Interacting age graphic dark energy models in non-flat universe. Phys Lett. B 680. 2009; 113. doi: 10.1016/j.physletb.2009.08.051   
6. Padmanabhan T. cosmological constant-the weight of the vaccum. Phys Rept. 2003; 380: 236. doi: 10.1016/S0370-1573(03)00120-0   
7. Copeland E J. Int. J. Mod. Phys D 57. 1998; 4686   
8. NojiriS, Odintsov SD. Modified gravity with negative and positive powers of curvature Unification of inflation and cosmic acceleration . Phys Rev D 68. 2003; 68. doi: 10.1103/PhysRevD.68.123512   
9. Harko T. f (R,T)gravity. Phys. Rev. D 84. 2011; 84. doi: 10.1103/PhysRevD.84.024020   
10. Brans CH, Dicke RH. Mach’s Principle and a Relativistic Theory of Gravitation. Phys Rev 124. 1961; 925. doi: 10.1103/PhysRev.124.925   
11. Saez D, Ballester VJ. A simple coupling with cosmological implications. Phys Lett. A 113. 1986; 467. doi: 10.1016/0375-9601(86)90121-0   
12. Adhav KS. LRS Bianchi type-I cosmological model in f( R, T) theory of gravity. Astrophys Space Sci. 339. 2012; 365. doi: 10.1007/s10509-011- 0963-8   
13. Chandel S, Ram S. Anisotropic Bianchi type-III perfect fluid cosmological models in f (R, T) theory of gravity. Ind.J.Phys. 2013; 87: 1283   
14. Reddy DRK. Kaluza-Klein Cosmological Model in f(R,T) Gravity. Int. J. Theor Phys. 2012; 51: 3222. doi: 10.1007/s10773-012-1203-x   
15. Sharif M, Zubair MJ. Anisotropic Universe Models with Perfect Fluid and Scalar Field in f(R,T) Gravity. Phys. Soc. Jpn. 2012; 81: 114005. doi: 10.1143/JPSJ.81.114005   
16. Rao VUM, Neelima D. Perfect-fluid Einstein-Rosen universe in f(R,T) gravity. Eur Phy J.Plus. 2013; 128: 35. doi: 10.1140/epjp/i2013-13035-y   
17. Reddy DRK. Bianchi type-III Dark Energy Model in f(R,T) Gravity. Int J Theor Phys. 2013; 52: 239. doi: 10.1007/s10773-012-1325-1   
18. Mishra B. Non-static cosmological model in f(R,T) gravity. Astrophys Space Sci. 2015; 359: 15. doi: 10.1007/s10509-015-2469-2   
19. Aditya Y. Some Bianchi type generalized ghost piligrim dark energy models in general relativity. Astrophys. Space Sci. 2016; 361: 56. doi: 10.1007/s10509-016-2731-2   
20. Rao VUM. Anisotropic Bianchi Type-V I h Perfect Fluid Cosmological Models in a Modified Theory of Gravity. Prespacetime J. 2015 ; 6: 947   
21. Santhi MV. Bulk viscous string cosmological models in f(R) gravity. Can J of Phys. 2017; 95(2): 136. doi: 10.1139/cjp-2017-0256   
22. Ramesh G, Umadevi S. LRS Bianchi type-II minimally interacting holographic dark energy model in Saez-Ballester theory of gravitation. Astrophys Space Sci. 2016; 361: 2. doi: 10.1007/s10509-015-2645-4   
23. Samanta GC, Dhal SN. Higher Dimensional Cosmological Models Filled with Perfect Fluid in f( R, T) Theory of Gravity. Int J Theor Phys. 2013; 52: 1334. doi: 10.1007/s10773-012-1449-3   
24. Kaluza T. To the problem of physics. Sitz Preus Akad WissPhy-Math K. 1921; 1: 966   
25. Klein OZ. Quantum Theory and Five-Dimensional Theory of Relativity. magazine for physics. 1926; 37: 895. doi: 007/BF01397481   
26. Overduin JM, Wesson PS. Kaluza-Klein gravity. Phys Rep. 1997; 283: 303. doi: 10.1016/S0370-1573(96)00046-4   
27. Lee HC. An Introductin to Kaluza Klein Theories. World Scientific, Singapore 1984.   
28. Appelquist T. Modern Kaluza-Klein theories. Addison-Wesley. Reading. 1987.   
29. Darabi F. Dirac quantization of noncommutative Abelian Proca fieldar. Xiv:1101.0666v1. 2011. doi: 10.1139/p2012-040   
30. Santhi MV. Kaluza-Klein Cosmological Models With Two Fluids Source in Brans-Dicke Theory of Gravitation. The African Review of Phys. 2016; 11: 0029   
31. Santhi MV. Two-Fluid Scenario for Higher Dimensional Dark Energy Cosmological Model in Saez-Ballester Theory of Gravitation. Prespacetime Journal. 2016; 7: 293   
32. Jamil M, Debnath U. FRW Cosmology with Variable G and Λ. Int J TheorPhys. 2011; 50: 1602. doi: 10.1007/s10773-011-0670-9   
33. Khadeka GS. Kaluza-Klein Type Robertson Walker Cosmological Model with Dynamical Cosmological Term Λ. Int J Theor Phys. 2008; 47: 1751. doi: 10.1007/s10773-007-9617-6   
34. Ozel C. Kaluza-Klein Type Cosmological Model with Strange Quark Matter. Adv Stud TheorPhys. 2010; 4: 117   
35. Sharif M, Farida K. Kaluza-Klein cosmology with varying G and Λ. Astrophys Space. Sci. 2011; 334: 209. doi: 10.1007/s10509-011-0711-0   
36. Berman MS. A special law of variation for Hubble’s parameter. Nuovo Cimento B .1983; 74: 182. doi: 10.1007/BF02721676   
37. Berman MS, Gomide FM. Cosmological models with constant deceleration parameter. General Relativity and Gravitation.1988; 20: 191. doi: 10.1007/BF00759327   
38. Akarsu O, Dereli T. Cosmological Models with Linearly Varying Deceleration Parameter. Int J Theor Phys. 2012; 51: 612. doi: 10.1007/s10773-011-0941-5   
39. Sarkar S. Holographic dark energy with linearly varying deceleration parameter and escaping big rip singularity of the Bianchi type-V universe. Astrophys Space Sci. 2014; 352: 859. doi: 0.1007/s10509-014-1920-0   
40. Sahoo PK, Sivakumar M. LRS Bianchi type-I cosmological model in f( R, T) theory of gravity with Λ( T). Astrophys Space Sci. 2015; 357: 60. doi: 10.1007/s10509-015-2264-0   
41. Santhi MV. Anisotropic magnetized holographic Ricci dark energy cosmological models. Candian J of Phys. 2017; 95(4): 381. doi: 10.1139/cjp-2016-0781   
42. Caldwell RR. Phantom Energy: Dark Energy with w<−1 Causes a Cosmic Doomsday. Phys Rev Lett. 2003; 9. doi: 10.1103/PhysRevLett.91.071301   
43. Cunha JV. Kinematic constraints to the transition redshift from supernovae type Ia union data. Phys Rev D Part Fields. 2009; 79: 047301. doi: 10.1103/PhysRevD.79.047301