Review Article
Structure of the Universe
BScE, DULE, 23 Park Ave, Saint John, NB E2J 1R2, Canada
*Corresponding author: Paul T E Cusack, BScE, DULE, 23 Park Ave, Saint John, NB E2J 1R2, Canada, Tel: +1-506-652-6350, E-mail: St-michael@hotmail.com
Received: November 17, 2018 Accepted: November 27, 2018 Published: January 3, 2019
Citation: Cusack PTE. Structure of the Universe. Int J Cosmol Astron Astrophys. 2019; 1(1): 4-6. doi: 10.18689/ijcaa-1000102
Copyright: © 2019 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, we consider how the universe may have come to exhibit the structure that it does. Viz uniform distribution on mass throughout and an ellipsoid shape. This finding doesnʼt agree with previous theories which have the universe as expanding. In fact, the universe is being compressed and mass results.
Keywords: Mass; Magnetic Force; Ellipsoid; Universe
Introduction
In this brief paper, we examine why the universe has mass evenly distributed or whey it is uniform. We consider also why mass terminates at 118 elements. And finally, we consider why the universe may be shaped as an ellipsoid [1]. Uniformity Distributed Mass The structure of the universe is said to be rather uniform throughout except for black holes or the like. It is much like raindrops on the surface of a glass window. The S.F. (Superfroce) provides for enough energy to allow for the mass of the periodic table of the elements. Space is formed and the universal moment is embedded into the very structure of the universe (Figure 1).

F=G M1 M2/ R2
S.F.=Superforce=8/3
Let M1=1
FR2/ [M1M2]=6.67
R2/ M2=3998~0.400~Re
R2/M=Re=I.F. V.F
R2/4.486=402
R2 =180
R=0.1342
R=1-0.8667
=0.1334
=space
4.482/2 (1/√2)=1583
=Moment
=Mom.
=1-sin 1
Magnetic Forces and Mass
When an experimenter pushes two magnets of like poles together, there is resistance up to a point. Then the resistance is overcome and there is no opposing forces remaining in the bars. It is like that with the universe too. When the resistance of energy being squeezed in to mass is overcome, mass results stored energy (Figure 2).

F=Ma
F=8/3
Let v=c=2.9979~3.0
a=1/√2
Let M=1
Mad/t=8
M(1/√2)3=8
1/{8 √2)(3)=1/M
M1/M=2.65~S.F
265=1/4.482 x
=118.77=Mass of Periodic Table of the Elements.
F=Ma
(4,482)(1/√2)
=3.169
~π
F=8/3=π
8=3π
3π/8=118.84=Mass
Ellipsoid Universe
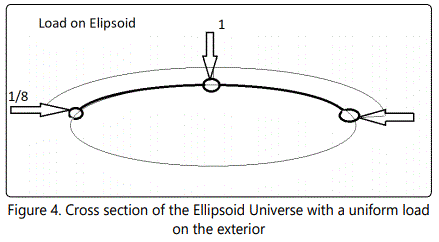
The Ellipsoid Universe results from the gravitational forces (Figures 3 and 4). We use the equation for an ellipsoid to yield the gravitational constant.
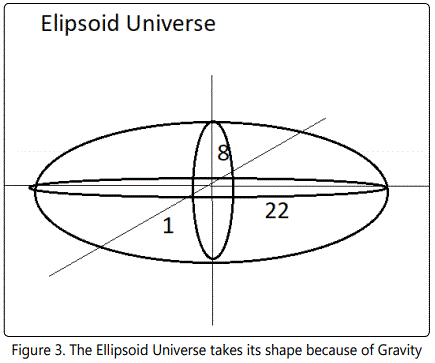
66 ×24 ×3=1584=1-sin1=Mom.
√[12+82+222]=23.4=Ln π=Ln t
y=yʼ
y=Ln t
yʼ=1/t=E
dθ/dt=dθ/ds where t=s
π/2/8=π/16=196.3=∞=19.63%
π/2 /22=71.4%
Ln (1/8)=Lm (0.125)=
0.125=ex
x=Ln 0.25
x=2.08
0.208 x 19.63=408.3 ~Re
0.208 x 71.4%=148~1.5 Mass Gap
(1.5 x 66) +(402 x 24)=1 Ellipsoid
Ellipsoid
x2/A2+y2/B2=z2/C2=1
x=s=▯(4/3)
x2/24+y2/66=Lx%=1
This reduces to:
4356x2 +576y2=576(4356)=250.9=Period T
T=1/t=E
3356 1/E2-1/E=E-E2
This reduces to E4-E3-E+3356=0
Let E=1
-1+0.3356=0.664~G=6.67
Conclusion
We see that the universeʼs shape and mass distribution are determined by AT Math considerations.
References
- Cusack PTE. Astrotheology, Cusackʼs Universe. J. Phys. Math. 2016; 7(2): 8.


