Abstract

More than forty transition metal carbonyls mainly bimetallic ones have been categorized using skeletal numbers. Their cluster valence electrons (CVE) were calculated using six different equations which had been discovered and consolidated during the course of the studies on chemical clusters over a period of time. These equations were easy to formulate after the discovery that chemical clusters form natural series which follow arithmetic progressions. With more scrutiny, it will be possible to find other equations which would help in calculating CVE. The categorization parameter, K^*=C^y+D^z is a useful concept in analyzing clusters. Regardless of how it was arrived at for transition metals or main group elements, it conveys vital information. From, you can know how many skeletal elements are in a cluster, the cluster valence electrons can be calculated, the type of series and clan of the cluster can be determined and the possible geometrical skeletal structure of the cluster can be predicted, among others. The isomeric and graphical skeletal structures of some of the clusters were constructed.

Keywords: Fundamental equations; Cluster valence; Graphical structure; Isomeric structure; Genesis electrons; Capping elements; Categorization.

Introduction

Cluster valence electrons (CVE) play a significant role in chemistry especially in polyhedral clusters where certain shapes of clusters are associated with specific number of cluster valence electrons [1-3]. Furthermore, the octet rule (8 electrona), and 18 electron rules are well known for chemical stability in main group and transition metal elements respectively [4,5]. The 16 electron clusters or fragments are also important in catalysis [6]. On closer and deeper analysis of the sequence of cluster formulas especially the transition metals, it was discerned that their cluster valence electrons form numerous fascinating series [7,8]. Consequently, a series formula S=14n+q (where n=number of skeletal elements in a cluster and q=is a variable) was designed to express this phenomenon for transition metals. A corresponding formula S=4n+q for the main group elements [9]. Further understanding of clusters revealed that the formula S=4n+q could be adopted to analyze and categorize clusters for both main group and transition metals [7-9]. Relatively recently, skeletal numbers were developed for the periodic table elements of the main group as well as the transition metals and ligands [10,11]. The skeletal numbers have been extremely useful in analyzing and categorizing clusters into CLANS and FAMILIES [12,13]. What is interesting is that using skeletal numbers a cluster formula with or without ligands is decomposed into a whole number, given the symbol K. By knowing the number of skeletal elements (n) the symbol is referred to as the K(n) parameter [14].

Let us consider a few examples to illustrate the application of the skeletal numbers

i. F=Os₁₀(CO)₂₆^2-:

Osmium skeletal element has a K value of 5 and the CO ligand has a K value of -1 while the negative charge behaves as a ligand since it is adding an electron (-1) or two electrons (-2) or more. For each electron added K=-0.5. The cluster number K=10[5]-26[1]-2[0.5]=23, n=10(the ten osmium skeletal elements and hence K(n) parameter=23(10). From earlier work, the cluster series is given by S=4n+q, and K=2n-½ q. We know K=23 and n=10, hence K=2n-½ q; 23=2[10]-½ q, ½ q=20-23=-3, q=-6. Therefore the cluster series will be S=4n+q=4n-6 and K=2n+3, Kp=C⁴C[M6]. This symbol means that there will be 4 capping skeletal elements and the remaining 6 will form and octahedral cluster around which the capping occurs. This is what is observed [15], during the study of K(n) sequences, it was discovered that the nuclear elements are also capped on electrons. Hence, a categorization symbol K^*=C^y+D^z was adopted. In this case, the cluster, Os₁₀(CO)₂₆^2- is represented by the symbol K^*=C⁴+D⁶; y=4, z=6.

Furthermore, it was also discovered that a number of equations to calculate the cluster valence electrons had emerged. These equations are simultaneously being used in this paper for comparative purposes and to allow the reader to know that the cluster valence electrons are inherent within the cluster formula itself. These equations are now demonstrated using this cluster under study.

ii. E=S=14n+q=14n-6. When n=10, then VE=14[10]-6=134.

This can easily be verified from the value obtained from the cluster formula itself, F= Os₁₀(CO)₂₆^2-: In general, K^*=C^y+D^z

In this case, K^*=C⁴+D⁶=C^y+D^z, y=4, z=6

iii. VF=10[8]+26[2]+2=134 from the cluster formula (this is a traditional method that can simply be used as a check)

iv. VE=18n-2K, n=10, K=23, hence VE=18[10]-2[23]=134

v. VE=VE0+12n, VE0 is the number of cluster valence electrons when n=0.

VE0 can readily be deduced by monitoring the sequence of the variation of the series as indicated in table 1. This value is 14(n=0) or it can easily be calculated from K(n)=-7(0) and substituting these in the equation VE=18n-2K=18[0]-2[-7]=14. Also since the CLAN of the series is D^z=D⁶, z=6; VE0=2z+2=2[6]+2=14. Thus, knowing VE0 and n=10, we can easily calculate VE=VE0+12n=14+12[10]=134.

vi. We can also calculate the cluster valence electrons from the equation VE=VE0+12y+12z=14+12[4]+12[6]=134.

This equation combines the GENESIS ELECTRON VEO, THE CAPPING ELECTRONS, C^y AND THE NUCLEAR CAPPING ELECTRONS D^z.

vii. Lastly, we can also use the equations VE=12y+14z+2=12[4]+14[6]+2=134
Equations are inter-related.
Note that the first 2 equations are inter-related and so are the last 3 equations.
S=VE=14n+q (i)
K=2n-½ q (ii)
We can re-arrange (ii) as q=4n-2K (iii)
Substituting the value of q in (i), we get
VE=14n+[4n-2K]=18n-2K (iv)

When the sequence of the K(n) parameters and their corresponding cluster valence electrons, it was found that they form well-organized sequence of INFINITE ARITHMETICAL PROGRESSIONS with no beginning and no end [12,13].

It made chemical sense to start the series of clusters at the GENESIS POINT, VE0 (n=0).

VE=VE0+12n (v)

VE=VE0+12y+12z (vi)

VE=VE0+12y+12z=VE0+12(y+z)…(vii) and since y+z =n, then the equation becomes, VE=VE0+12n……(viii) the same as in (v).

VE=VE0+12Y+12z…(vi). But VE0=2z+2 from series relationship and hence

VE=(2z+2)+12y+12z=12y+14z+2 (ix).

These equations will be applied as much as possible in the examples given in this article to highlight their significance.

In this case the D⁶ fragments of the closo system start capping when VE0=14 already. Therefore the closo valence electrons will be VE=14+12n=14+12[6]=86,the valence electrons always cited for an octahedral geometry of a D⁶ fragment.

ii. F=Pd₃₅(CO)₂₃L₁₅:K=35[4]-23-15=102
K(n)=102(35)
2[35]-102=-32
S=4n-64
K=2n+32
Kp=C³³C[M2]
K^*=C³³+D²; y=33,z=2
VE0=2z+2=2[2]+2=6

From the above information, we can derive 6 fundamental equations for calculating CVE.

• VE=18n-2K=18[35]-2[102]=426
• VE=14n-64=14[35]-64=426
• VE=VE0+12n=6+12[35]=426
• VE=VE0+12y=12z=6+12[33]+12[2]=426
• VE=12y+14z+2=12[33]+14[2]+2=426
• VE=VEDz+12n=VED2+12y=30+12[33]=426

In the categorization symbol, K^*=C³³+D², the clan D² (S=4n+2, K=2n-1=2[2]-1=3) represents two skeletal elements bound by a triple bond. Since Pd(K=4, V=8), when 3 of the 8 available linkages are used up in the triple bond, then 5 linkages will remain available to linking up with other skeletal elements. Hence, we can design a nuclear model based on 5 linkages for capping the remaining 33 skeletal elements this concept is illustrated in figure 1.

iii. F=Pd₃₀(CO)₂₆L10: K=30[4]-26-10=84
K(n)=84(30)
2[30]-84=-24
S=4n-48
K=2n+24
Kp=C²⁵C[M5]
K^*=C²⁵+D⁵;y=25, z=5
VE0=2z+2=2[5]+2=12

With this information, we can calculate CVE in several ways;

• VE=18n-2K =18[30]-2[84]=372
• VE=14n-48=14[30]-48=372
• VE=VE0+12n=12+12[30]=372
• VE=VE0+12y+12z=12+12[25]+12[5]=372
• VE=VEDz+12y=VED5+12y=72+12[25]=372

VED5=14z+2=14[5]+2=72

• VE=12y+14z+2=12[25]+14[5]+2=372

iv. F=Pd₅₉(CO)₃₂L₂₁:K=59[4]-32-21=183
K(n)=183(59)
2[59]-183=-65
S=4n-130
K=2n+65
Kp=C⁶⁶C[M-7]
K^*=C⁶⁶+D^-7;y=66,z=-7
VE0=2z+2=2[-7]+2=-12

• VE=18n-2K=18[59]-2[183]=696
• VE=14n-130=14[50]-130=696
• VE0+12n=-12+12[59]=696
• VE0+12y+12z=-12+12[66]+12[-7]=696
• VE=12y+14z+2=12[66]+14[-7]+2=696
• VE=VEDz+12y=VED-7+12y=-96+12[66]=696

VED-7=14z+2=14[-7]+2=-96

v. F=Pd₁₆₅(CO)₆₀L₃₀:K=165[4]-60-30=570
K(n)=570(165)
2[165]-570=-240
S=4n-480
K=2n+240
Kp=C²⁴¹C[M-76]
K^*=C²⁴¹+D^-76;y=241, z=-76
VE0=2z+2=2[-76]+2=-150

• VE=18n-2K=18[165]-2[570]=1830
• VE=14n-480=14[165]-480=1830
• VE=VE0+12n=-150+12[165]=1830
• VE=VE0+12y+12z=-150+12[241]+12[-76]=1830
• VE=12y+14z+2=12[241]+14[-76]+2=1830
• VE=VEDz+12y=-1062+12[241]=1830

VED-76=14z+2=14[-76]+2=-1062

Categorization of Clusters and Cluster Clan Trees

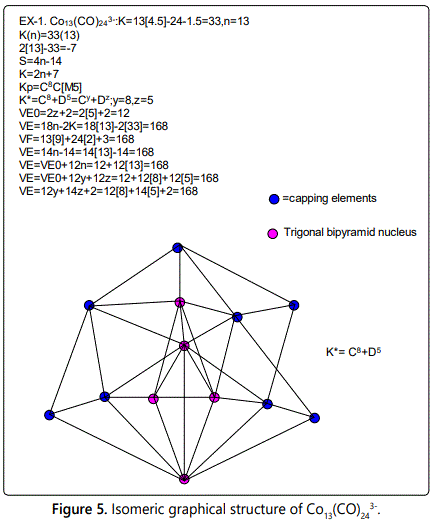
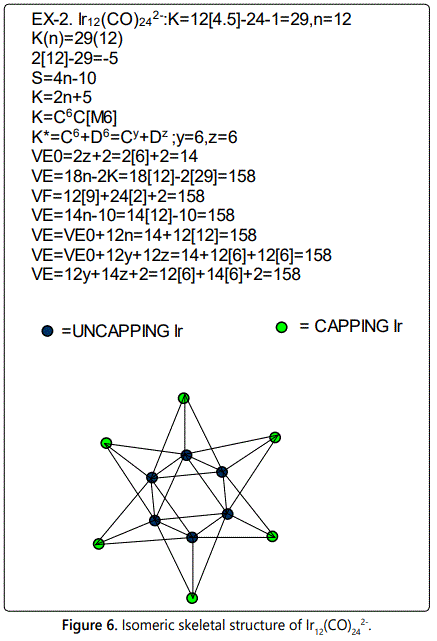
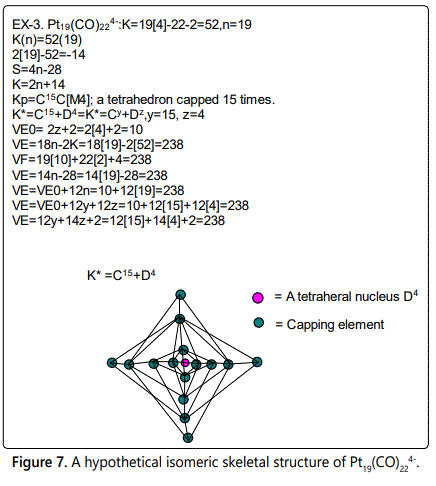
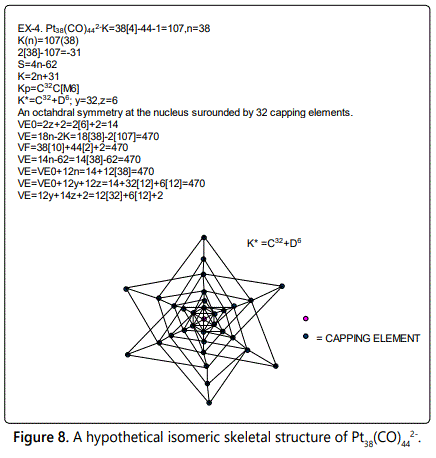
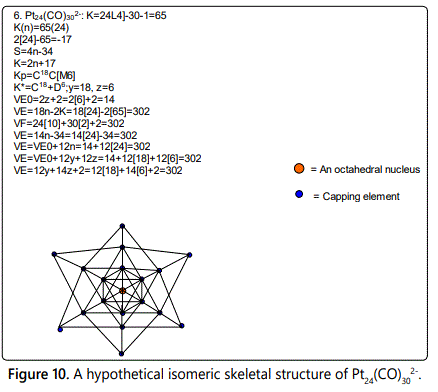
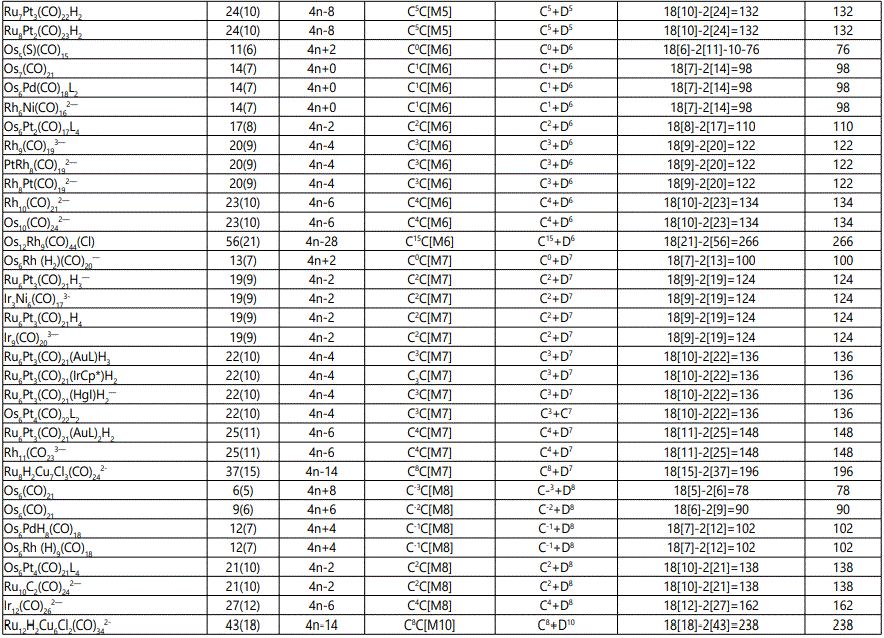
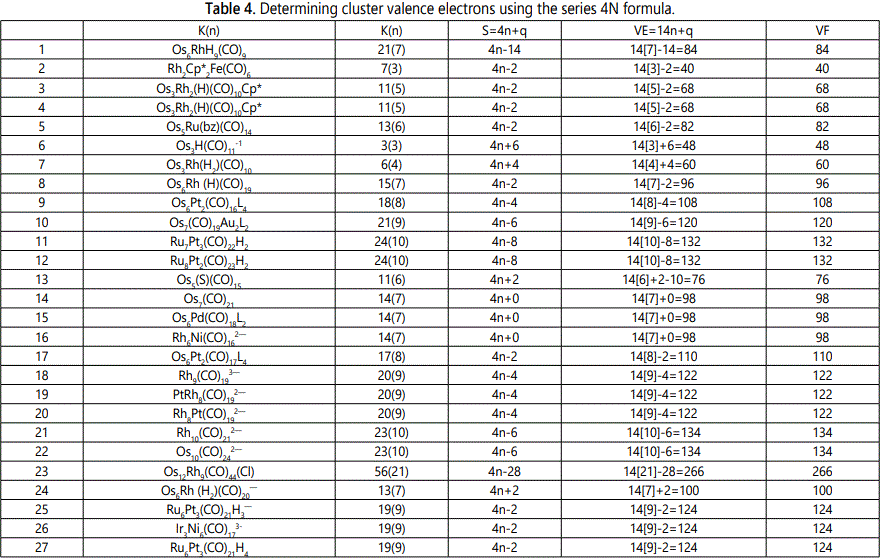
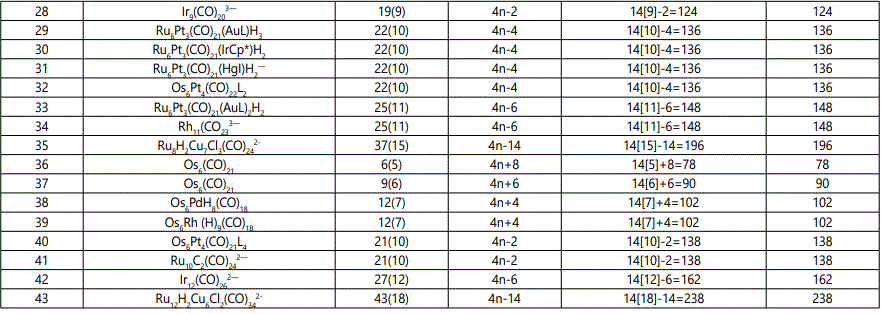
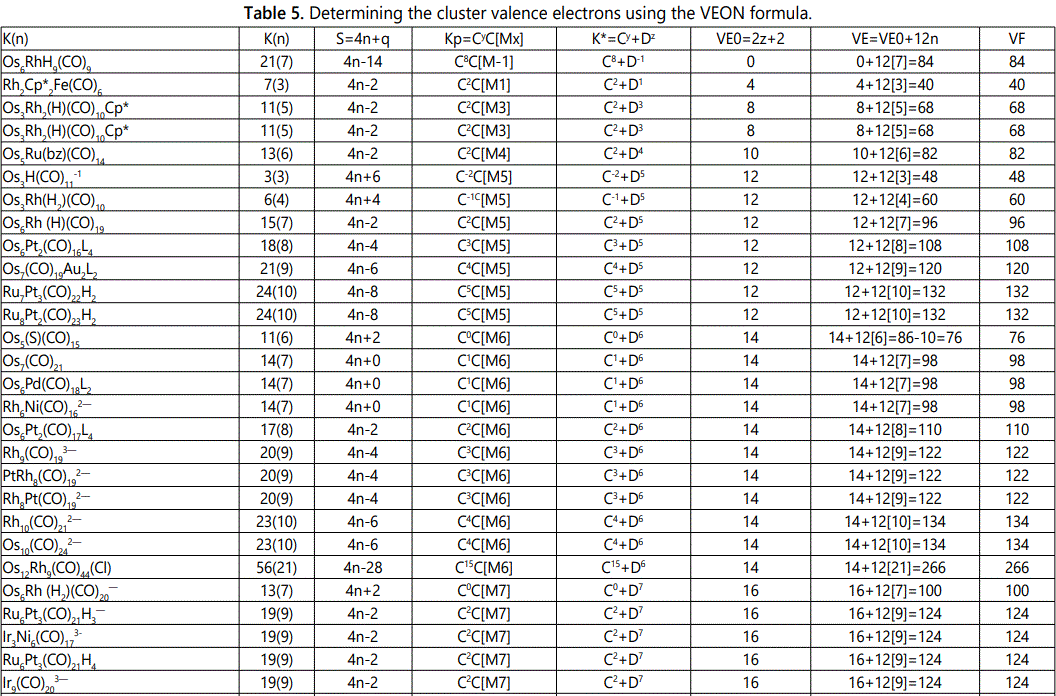
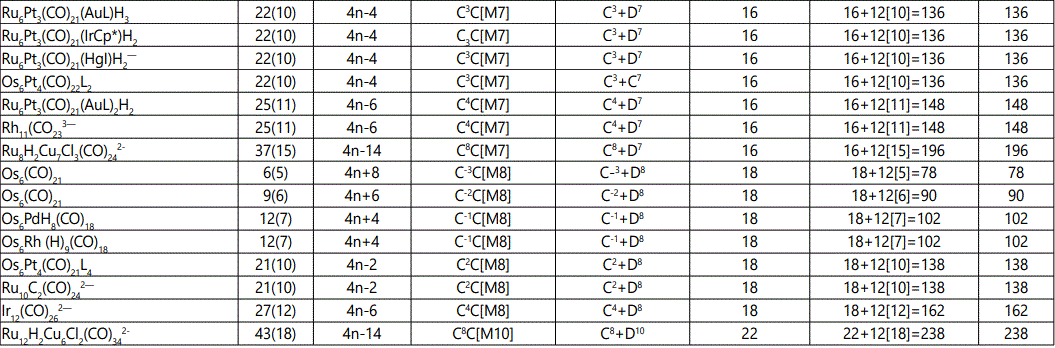
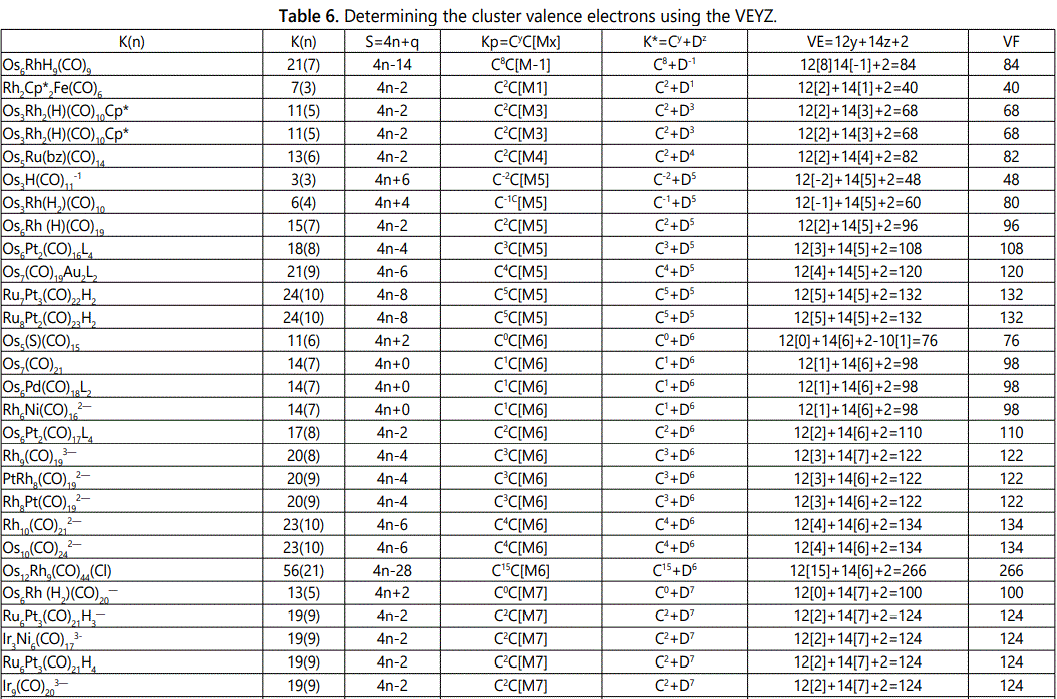
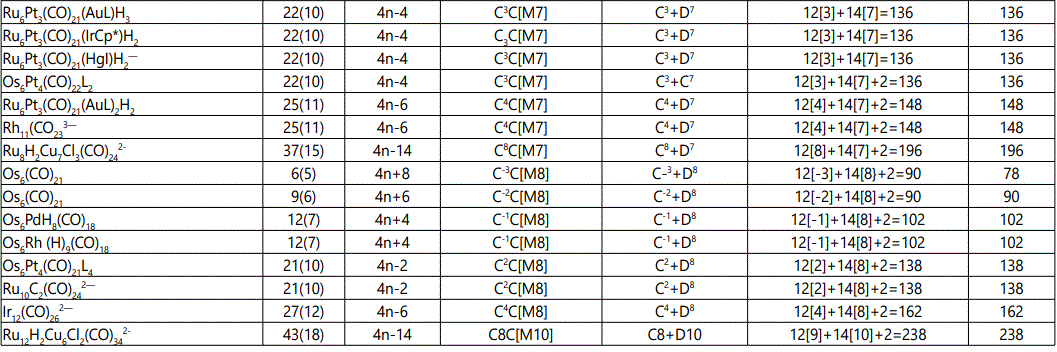
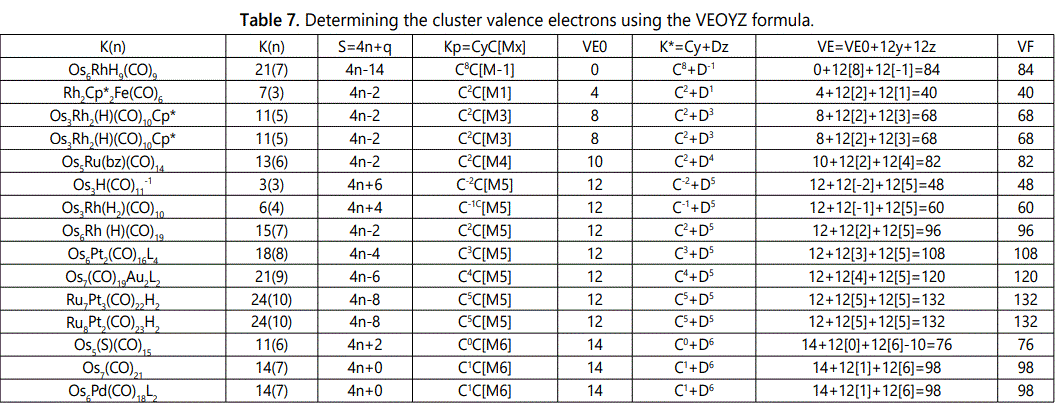
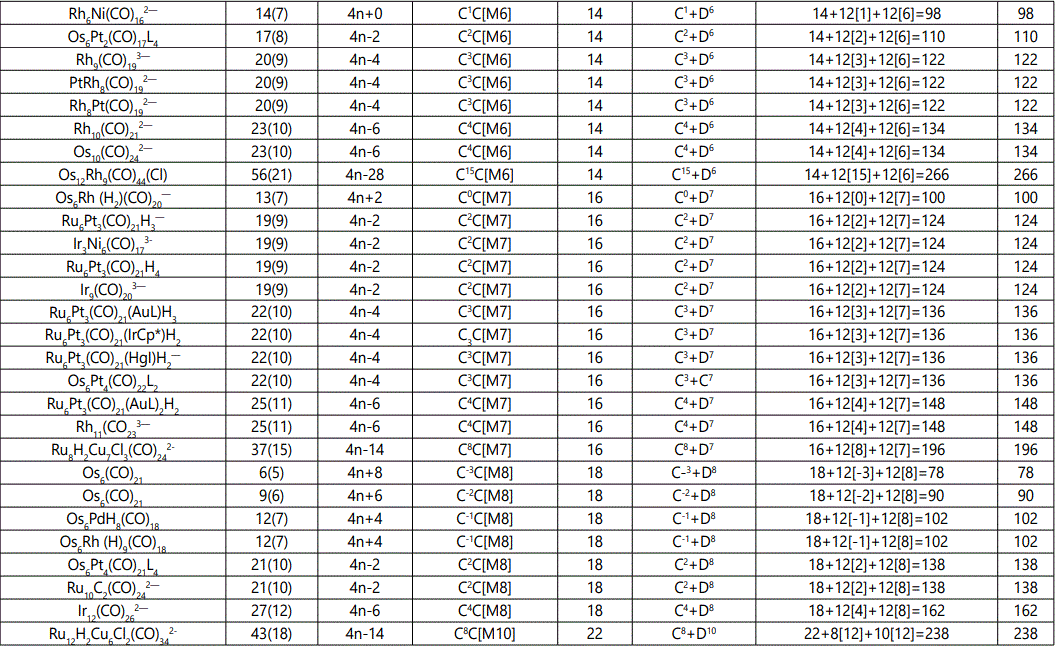
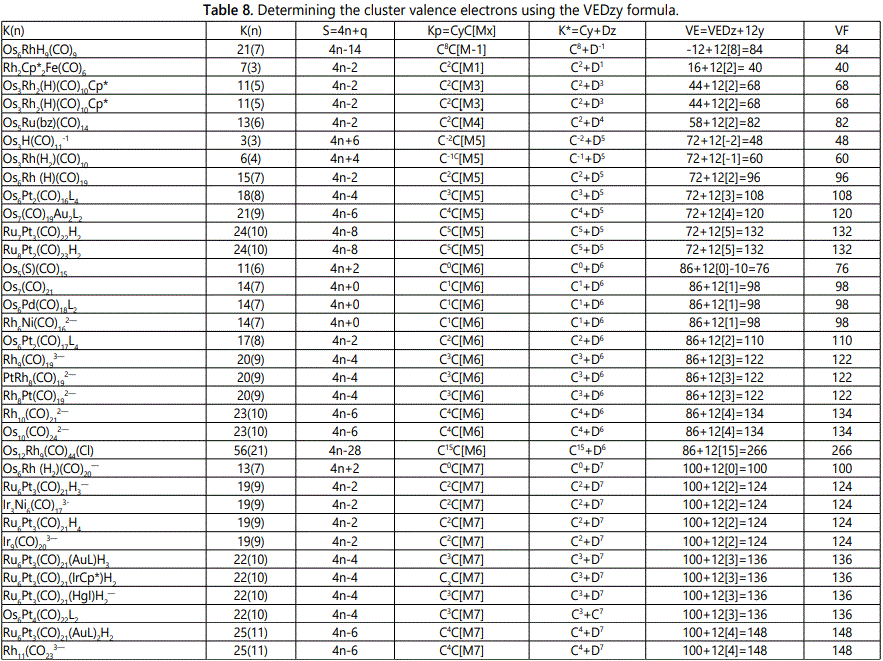
Skeletal numbers are very easy and quick in categorizing a given chemical cluster from the main group or transition metals [10-14,16]. A cluster formula is decomposed usually into a whole number using skeletal elements. Knowing the number of skeletal elements in the cluster formula, the family series S=4n+q is readily derived. From it the categorization parameter K^*=C^y+D^z is obtained. The D^z represents the clan of the cluster and the C^y represents the family of the cluster. A general scheme of a cluster clan is shown figure 2 represents a single clan. In other words, a single vertical line D^z is a representative of a single clan. Figure 3 represents just a portion of a whole range of infinite universe of clusters. Table 2 gives us a small portion of a D6 (based on an octahedral closo fragment clan tree and some of the known clusters. According to the categorization of clusters adopted according to the 4N series, the closo clusters, S=4n+2 (C⁰ clusters) have taken up the central position as reference cluster points. Using Figure 0 as an illustration, those clusters below C⁰ have one or more skeletal elements to remaining in order for them to attain a closo status. Those clusters which have one or more cluster elements beyond C⁰ are capped complexes. The valence electrons of the closo fragments have been calculated. These are given in table 3. More clusters were categorized into the clan and family format K^*=C^y+D^z. These are illustrated in the examples EX-1 to EX-6 the possible isomeric graphical structures of some of the clusters are given in figures 5-10. The isomeric structures of examples EX-1 to EX-6 are shown in figures 5-10. Due to the ease of numerically categorizing chemical clusters, more than 40 transition metal carbonyl clusters were analyzed. More importantly, during the study of the array of many chemical clusters, SIX FUNDAMENTAL EQUATIONS for calculating the cluster valence electrons were exposed. Hence a single table for demonstrating the use of each new CVE equation has been constructed giving a total of 6 tables 3-8. The clusters have been arranged into their CLAN-FAMILY MATRIX category.

Possible Shapes of Selected D^z Fragments

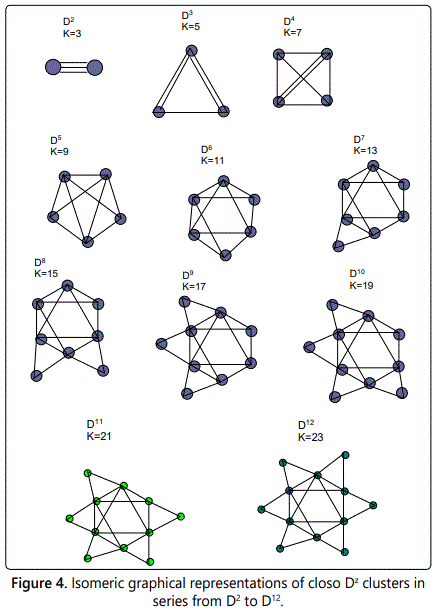
The D^z clusters are all family members of the series S=4n+2 (closo systems). The number of skeletal linkages are given by K=2n-1. Let us start with D², K=2n-1=2[2]-1=3. This means, this is a cluster of two skeletal elements bound by 3 linkages. All the D^z CLAN clusters belong to the same closo family and K- values differ by 2 units. In this case, D³(K=5), D⁴(K=7), D⁵(K=9), D⁶(K=11) and so on. From one cluster to another, the number of linkages differs by 2. This is different from that of clan series whose linkages differ by 3.The possible isomeric skeletal shapes are given in figure 4 for D² to D¹².

More Examples Categorized

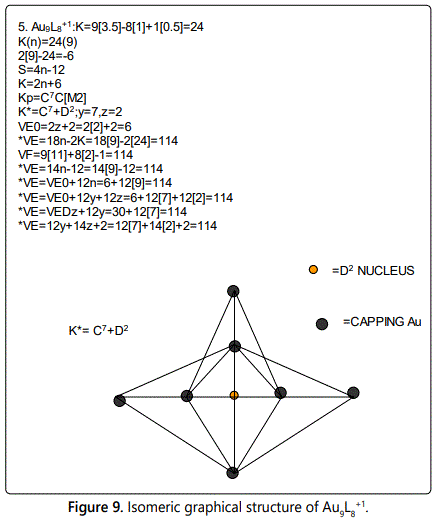
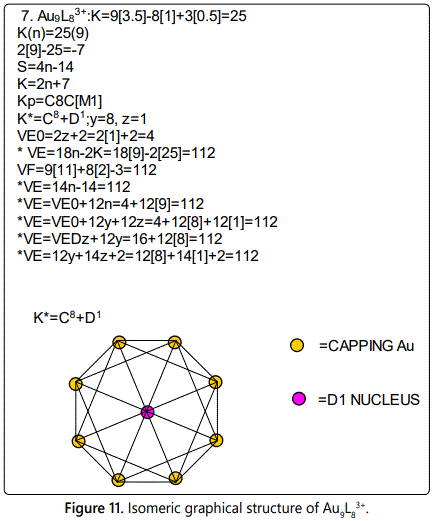
The cluster Au₉L₈³⁺(K^*=C⁸+D¹) was found to have 8 skeletal elements capping around one central skeletal element as predicted by the categorization parameter, K^* [17].

Results and Discussion

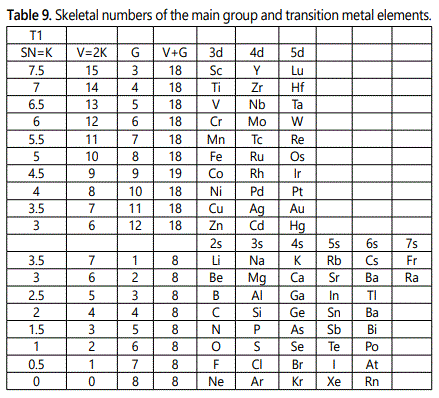
The use of skeletal numbers to categorize clusters is very new and therefore it is best to present them to the readers right at the beginning. These are shown in table 9. The skeletal elements may be regarded as equal partners in a cluster with or without the ligands working together to generate one cluster number (K) but may contribute to it differently using their respective skeletal numbers. Since the skeletal elements have ‘equal membership’ but may have different contributions ‘skeletal numbers’, the resultant cluster number can be expressed as K(n) parameter, where n represents the total number of skeletal elements in a cluster irrespective of the periodic table groups they come from.

Conclusion

The set of clusters analyzed indicate that the most prevalent ones are the D₅(VE0=12,VED5=72), D⁶(14,86) and D⁷(16,100) clans with characteristic baseline, and closo valence electrons enclosed. The power of skeletal numbers to penetrate a chemical cluster formula however complex it may look and extract its cluster valence electrons is clearly demonstrated. The six fundamental equations for calculating the cluster valence electrons without recourse to the traditional method have been exposed. Clearly, the cluster valence electrons are inherent within the cluster formula and can be accessed in various ways six of which have been identified. Inherent within the cluster is the fact that skeletal elements have a tendency to interact in such a way that the cluster number K is a whole number and the cluster valence electrons (CVE) is an even number. The skeletal elements along with their skeletal numbers obey strict and precise algebraic rules of the 4N series.

References

1. Housecroft CE, Sharpe AG. Inorganic Chemistry. 2nd Edition, Pearson, Prentice Hall, Harlow, England. 2005.   
2. Miessler G, Fischer P, Tarr D. Inorganic Chemistry. 5th Edition, Pearson Education, Inc., Upper Saddle River. 2014.   
3. Teo BK, Longoni G, Chung FRK. Applications of Topological ElectronCounting Theory to Polyhedral Metal Clusters. Inorg Chem. 1984; 23(9): 1257-1266. doi: 10.1021/ic00177a018   
4. Crabtree RH. The Organometallic Chemistry of the Transition Metals. 4th Edition, John-Wiley & Sons, New Jersey. 2005.   
5. Pyykko P. Understanding the eighteen-electron rule. J Organomet Chem. 2006; 691(21): 4336-4340. doi: 10.1016/j.jorganchem.2006.01.064   
6. Tolman CA. The 16 and 18 Electron Rule in Organometallic Chemistry and Homogeneous catalysis. Chem Soc Rev. 1972; 1: 337-353. doi: 10.1039/CS9720100337   
7. Kiremire EMR. The Application of the 4n Series Method to Categorize Metalloboranes. Int J Chem. 2016; 8(3): 62-73. doi: 10.5539/ijc.v8n3p62   
8. Kiremire EMR. Classification of Zintl Ion Clusters Using 4n Series Approach. Orient J Chem. 2016b; 32(4): 1731-1738. doi: 10.13005/ojc/320401   
9. Kiremire EMR. The categorization and Structural Prediction of Transition Metal Carbonyl Clusters Using the 14n Series Numerical Matrix. Int J Chem. 2016; 8(1): 109-125. doi: 10.5539/ijc.v8n1p109   
10. Kiremire EMR. The outstanding Applications of Skeletal Numbers to Chemical Clusters. Int J Chem. 2017; 9(3): 28-48. doi: 10.5539/ijc.v9n3p28   
11. Kiremire EMR. Boranes, Carboranes, Metalloboranes, Transition Metal Carbonyls, and Other Cluster Formulas Obey the Law of Skeletal Numbers and Their Valences. Amer J Chem. 2017; 7(4): 113-144. doi: 10.5923/j.chemistry.20170704.02   
12. Kiremire EMR. The Capping Theory of Chemical Elements and Clusters Based on 4N Series and Skeletal Numbers. Int J Chem. 2018; 10(4): 94-123. doi: 10.5539/ijc.v10n4p94   
13. Kiremire EMR. The Capping Theory of Chemical Elements and Clusters Based on 12N/4N Series. Int J Chem. 2018; 10(4): 130-154. doi: 10.5539/ijc.v10n4p130   
14. Kiremire EMR. The Six Silent Laws of Chemical Clusters. Am J Chem. 2017; 7(2): 21-41. doi: 10.5923/j.chemistry.20170702.01   
15. Hughes AK, Wade K. Metal-metal and metal-ligand bond strengths in metal carbonyl clusters. Coord Chem Rev. 2000; 197(1): 191-229. doi: 10.1016/S0010-8545(99)00208-8   
16. Kiremire EMR. A Hypothetical Model for the Formation of Transition Metal Carbonyl Clusters Based Upon 4n Series Skeletal Numbers. Int J Chem. 2016; 8(4): 78-110. doi: 10.5539/ijc.v8n4p78   
17. Mingos DMP. Gold Cluster Compounds: Are they materials in miniature? Gold Bull. 1984; 17(1): 5-12.