Abstract

In this paper, we found a new model for compact star with charged anisotropic matter distribution considering an extended version of the Chaplygin equation of state. We specify a particular form of the metric potential Z(x) that allows us to solve the Einstein-Maxwell field equations. The obtained model satisfies all physical properties expected in a realistic star such that the expressions for the radial pressure, energy density, metric coefficients, measure of anisotropy and the mass are fullywell defined and are regular in the interior of star. The solution obtained in this work can have multiple applications in astrophysics and cosmology.

Keywords: Einstein-Maxwell field equations; Chaplygin equation of state; Metric potential; Radial pressure; Measure of anisotropy.

Introduction

The study and description of static fluid spheres is an interesting area of research and one of great relevance in astrophysics due to formulation of the general theory of relativity [1,2]. One of the most important issues in general relativity is finding exact solutions to Einsteinʼs field equations in order to propose physical models of compact stars as suggested by Delgaty and Lake [3] who constructed several analytic solutions that describe static perfect fluid and satisfy all the necessary conditions to be physically acceptable [3]. These exact solutions have also made it possible the way to study cosmic censorship and analyze the formation of naked singularities [4].

In the construction of theoretical models of stellar objects, the research of Schwarzschild [5], Tolman [6] and Oppenheimer and Volkoff [7] are very important to be considered. Schwarzschild [5] found analytical solutions that allowed describing a star with uniform density, Tolman [6] developed a method to find solutions of static spheres of fluid and Oppenheimer and Volkoff [7] used Tolmanʼs solutions to study the gravitational balance of neutron stars. It is important to mention that Chandrasekharʼs contributions [8] in the model production of white dwarfs and in presence of relativistic effects and the works of Baade and Zwicky [9] fully propose the main physical concepts of neutron stars and also identify astronomic dense objects known as supernovas.

The presence of the electric field can modify the values for surface redshift, luminosity, density and maximum mass for stars. Bekenstein [10] considered that the gravitational attraction may be balanced by electrostatic repulsion due to electric charge and pressure gradient. Komathiraj and Maharaj [11] obtained new classes of exact solutions to the Einstein-Maxwell system of equations for a charged sphere with a particular choice of one of the metric potentials. Ivanov [12] has studied and developed a wide variety of charged stellar models. More recently, Malaver and Kasmaei [13] proposed a model of charged anisotropic matter with nonlinear equation of state.

It is well known the fact that the anisotropy plays a significant role in the studies of relativistic stellar objects [14-26]. The existence of solid core, presence of type 3A superfluid [27], magnetic field, mixture of two fluids, a pion condensation and electric field [28] are most important reasonable facts that explain the presence of anisotropy. Bowers and Liang [14] generalized the equation of hydrostatic equilibrium for the case of local anisotropy. Bhar et al. [29] have studied the behavior of relativistic objects with anisotropic matter distribution considering the Tolman VII form for the gravitational potential.

Many researchers have used a variety of analytical methods in order to try to obtain exact solutions of the Einstein-Maxwell field equations for anisotropic relativistic stars. It is very important to mention that the contributions of Komathiraj and Maharaj [11], Thirukkanesh and Maharaj [30], Maharaj et al. [31], Thirukkanesh and Ragel [32,33], Feroze and Siddiqui [34,35], Sunzu et al. [36], Pant et al. [37] and Malaver [38-41] needs to be considered in this field of research study. These studies suggest that the EinsteinMaxwell field equations are very important in the description of ultra compacts objects.

The development of theoretical models of stellar structures can consider several forms of equations of state [42]. Komathiraj and Maharaj [43], Malaver [44], Bombaci [45], Thirukkanesh and Maharaj [30], Dey et al. [46] and Usov [28] assume linear equation of state for quark stars. Feroze and Siddiqui [34] considered a quadratic equation of state for the matter distribution and specified particular forms for the gravitational potential and electric field intensity. MafaTakisa and Maharaj [47] obtained new exact solutions to the EinsteinMaxwell system of equations with a polytropic equation of state. Thirukkanesh and Ragel [48] have obtained particular models of anisotropic fluids with polytropic equation of state which are consistent with the reported experimental observations. Malaver [49] generated new exact solutions to the Einstein-Maxwell system considering Van der Waals modified equation of state with polytropic exponent. Bhar and Murad [50] obtained new relativistic stellar models with a particular type of metric function and a generalized Chaplygin equation of state. Recently Tello-Ortiz et al. [51] also found an anisotropic fluid sphere solution of the Einstein-Maxwell field equations with a modified version of the Chaplygin equation.

It is important to mention the fact that general relativity not only studies the interior of stellar objects, it also allows the analysis of different cosmological scenarios through the Einstein gravity theory as the existence of dark energy, dark matter, Phantom and Quintessence fields that were introduced to explain the accelerated expansion of the universe [51,52]. Chaplygin gas whose equation of state P = -B/ρ where P is the pressure, ρ the energy-density and B a positive constant, has been considered an alternative to the Phantom and Quintessence fields [50-53]. In order to adjust this equation of state to observational data has been rewritten as P = -B/ρ^ω with the parameter ω between 0 and 1 [53]. Furthermore, an extended version of the Chaplygin gas equation of state was proposed by Pourhassan [54] and its form is P = A ρ - B/ρ^ω where Aa positive parameter constrained to 0 < A < 1/3.

In this paper, we generated a new model of charged anisotropic compact object with the modified Chaplygin equation of state proposed for Pourhassan [54] and studied by Bernardini and Bertolami [55]. The modified Chaplygin equation of state is described by P = A ρ - B/ρ^ω where A, B, α are constants and 0 ≤ α ≤ 1. Using a particular form of gravitational potential Z(x) that is nonsingular, continuous and well behaved in the interior of the star, we can obtain a new class of static spherically symmetrical model for a charged anisotropic matter distribution. It is expected that the solution obtained in this work can be applied in the description and the study of internal structure of strange quark stars. The article is organized as follows: In the section “Einstein-Maxwell System of Equations”, we present Einstein-Maxwell field equations. In the section “Charged Anisotropic Model”, we make a particular choice for gravitational potential Z(x) and the electric field intensity and generated new models for charged anisotropic matter. In the section “Physical Requirements for the New Developed Model”, physical acceptability conditions are discussed. The physical properties and physical validity of these new solutions are analyzed in the “Physical Analysis” section. The conclusions of the results obtained are shown in the “Conclusion” section.

Einstein-Maxwell System of Equations

We consider a spherically symmetric, static and homogeneous space-time. In Schwarzschild coordinates, the metric is given by:

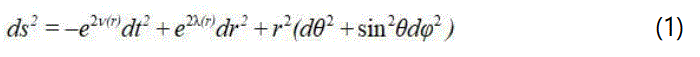
where v(r) and λ(r) are two arbitrary functions.

The Einstein field equations for the charged anisotropic matter are given by [30]:

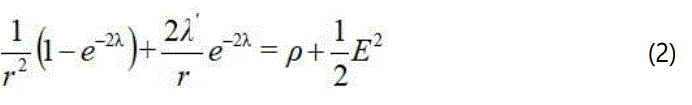
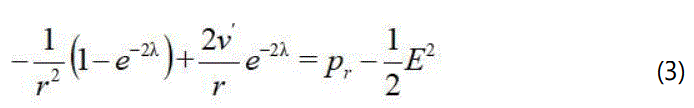
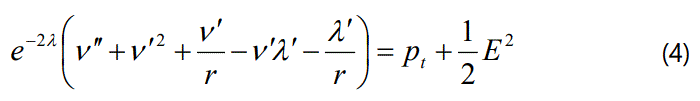
where ρ is the energy density, p_r is the radial pressure, E is electric field intensity, p_t is the tangential pressure and primes denote differentiations with respect to r. Using the transformations x=cr², Z(x)=e–^2λ(r) and A²*y²(x)=e^2v(r) with arbitrary constants A and c>0 suggested by Durgapal and Bannerji [56], the Einstein field equations can be written as:

σ is the charge density, Δ=p_t-p_r is the anisotropy factor and dots denote differentiations with respect to x. With the transformations of [56], the mass within a radius r of the sphere takes the form:

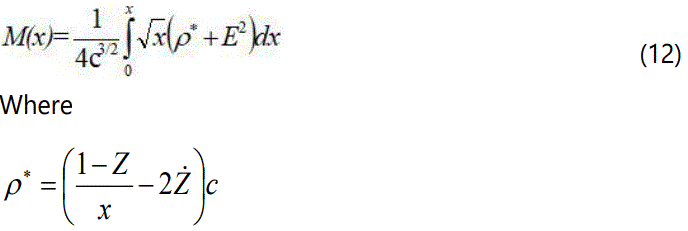
In this paper, we assume the following equation of state where the radial pressure and the density ρ are related to the following form:

with A and B as constant parameters, and α=1.

with A and B as constant parameters and ρ = ρ*+E².

Charged Anisotropic Model

In this work, we take the form of the gravitational potential Z(x) as _Z(x) =1-ax proposed for Malaver [38] and Thirukanesh and Ragel [48] where a is a real constant. This potential is regular at the origin and well behaved in the interior of the sphere. Following Ngubelanga et al. [57] for the electric field, we make the particular choice:

This electric field is finite at the center of the star and remains continuous in the interior. Using Z(x) and eq. (14) in eq. (6), we obtain

Substituting eq. (15) in eq. (13), the radial pressure can be written in the form:

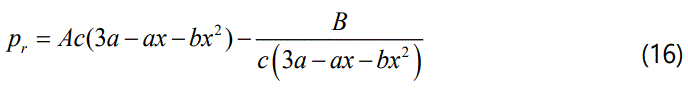
Using eq. (15) in eq. (12), the expression of the mass function is

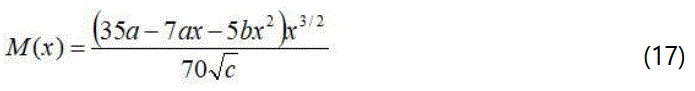
With eq. (14) and Z(x) in eq. (11), the charge density is

With equations (13), (14), (15) and Z(x), eq. (7) becomes:

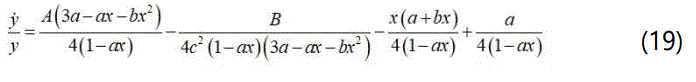
Integrating eq. (19) we obtain:

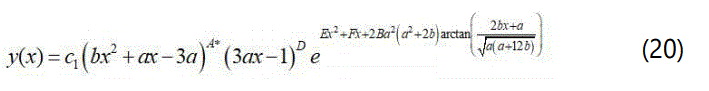
Where for the convenience we have let

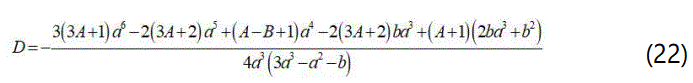
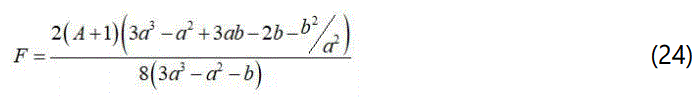
And c₁ is the constant of integration.

The metric functions e^2λ and e^2v can be written as:

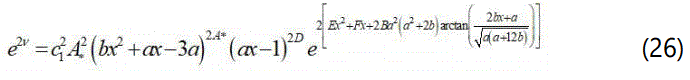
and the anisotropy factor Δ is given by:

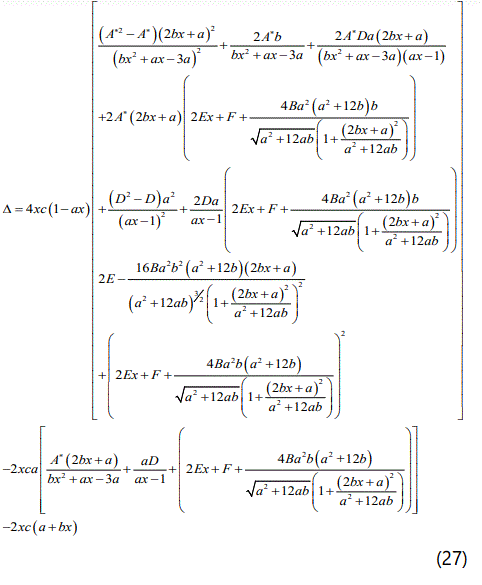
Physical Requirements for the New Developed Model

Following Delgaty and Lake [3], Thirukkanesh and Ragel [48] and Bibi et al. [58] for a model to be physically acceptable, it must satisfy the following conditions:

(i) Regularity of the metric potentials in the stellar interior and at the origin.

(ii) The radial pressure should be positive, decreasing with the radial coordinate and vanishing at the centre of the fluid sphere.

(iii) The energy density should be positive inside of the star and a decreasing function of the radial parameter. (iv) The radial pressure and density gradients dp_r/dr ≤ 0 and dρ/dr ≤ 0 for 0 ≤ r ≤ R.

(v) The causality condition requires that the radial speed of sound should be less than speed of light throughout the model, i.e. 0 ≤ dp_r/dr ≤ 1.

(vi) The radial pressure and the anisotropy is equal to zero at the centre of the fluid sphere Δ(r=0) =0.

(vii) The charged interior solution should be matched with the Reissner–Nordström exterior solution, for which the metric is given by:

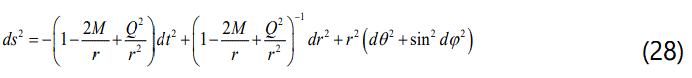
through the boundary r=R where M and Q are the total mass and the total charge of the star, respectively.

The conditions (ii), (iii) and (iv) imply that the radial pressure and energy density must reach a maximum at the centre and decreasing towards the surface of the sphere.

Physical Analysis

We now present the analysis of the physical characteristics for the new model. The metric functions e^2λ and e^2v and should remain positive throughout the stellar interior and in the origin e^2λ(0)=1,

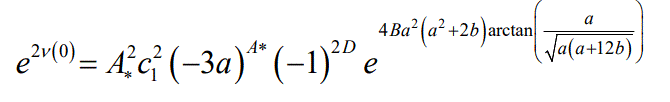
We note in r=0 that (e^2λ(r))^'_r=0 = (e^2v(r)'_r=0. This demonstrates that the gravitational potentials are regular at the centre r=0. The energy density and radial pressure are positive and well behaved inside the stellar interior. Also, we have the central density and pressure ρ(0)=3ac and p_r(0) = 3acA - B/3ac. According to the expression of radial pressure, p_r(0) will be non-negative at the centre as it is satisfied by the condition 3acA > B/3ac.

In the surface of the star r=R, we have p_r(r=R)=0 and

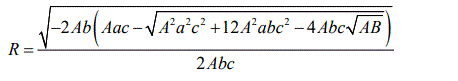
For a realistic star, it is expected that the gradient of energy density and radial pressure should be decreasing functions of the radial coordina r. In this model, for all 0<r<R, we obtain respectively:

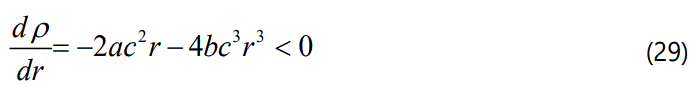
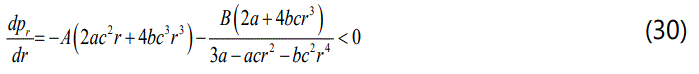
and according to the equations (29) and (30), the energy density and radial pressure decrease from the centre to the surface of the star.

From eq. (17), we have:

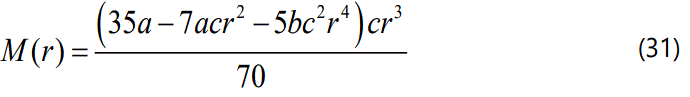
and the total mass of the star is:

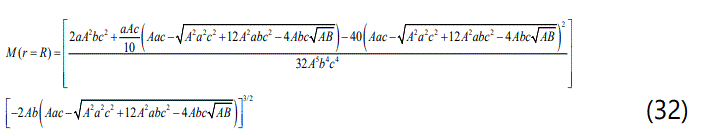
The causality condition demands that the radial sound speed defined as ν²_sr = ap_r/dρ should not exceed the speed of light and it must be within the limit 0 ≤ ν²_sr ≤ 1 in the interior of the star [3]. In this model, we have:

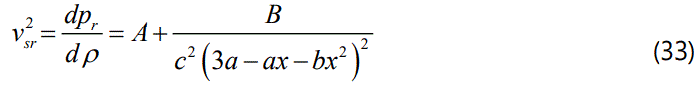
For the eq. (33) and with the transformations of Durgapal and Bannerji [56] we can impose the condition:

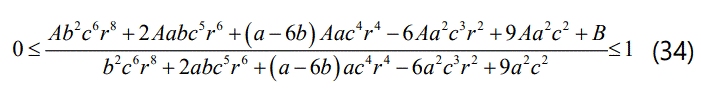
On the boundary r=R, the solution must match the Reissner–Nordström exterior space–time as:

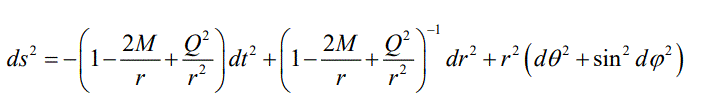
and therefore, the continuity of e^v and e^λ across the boundary r=R is

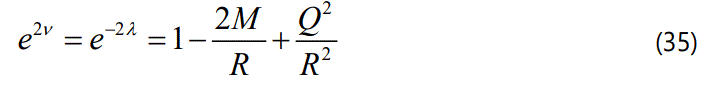
Then for the matching conditions, we obtain:

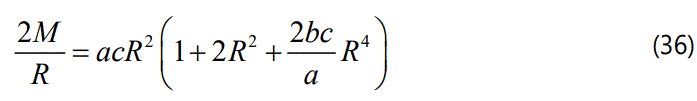
The figures 1-8 represent the graphs of pr, ρ, M(x), σ², Δ,v²sr, dp_r/dr and dρ/dr respectively with a=0.09, b=0.015, A=0.066, B=0.0000054, c=1 and stellar radius of r=1.46 km.

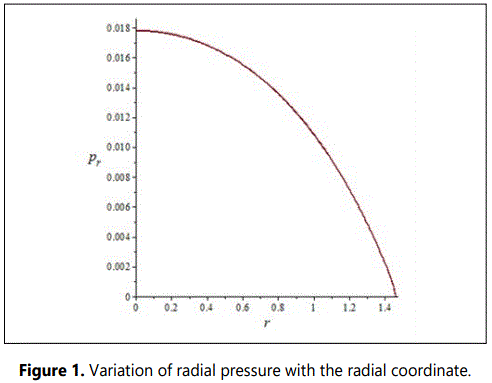
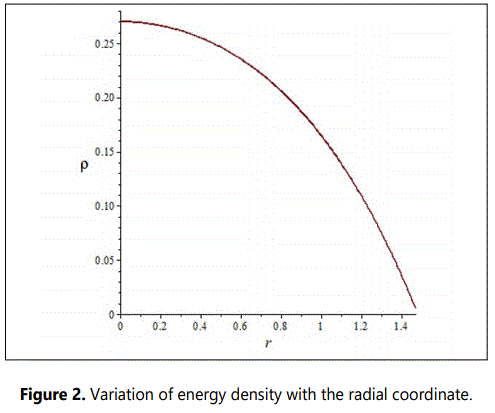
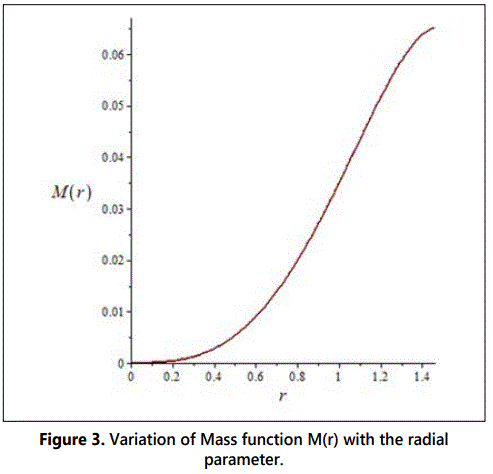
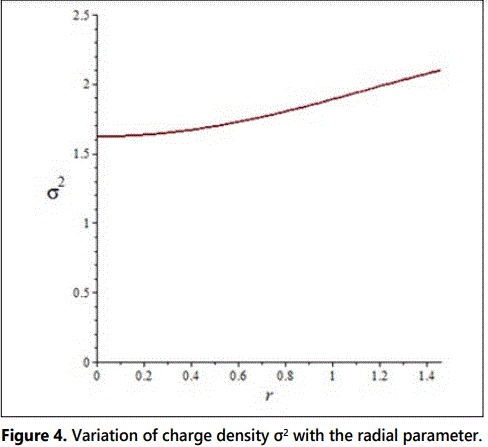
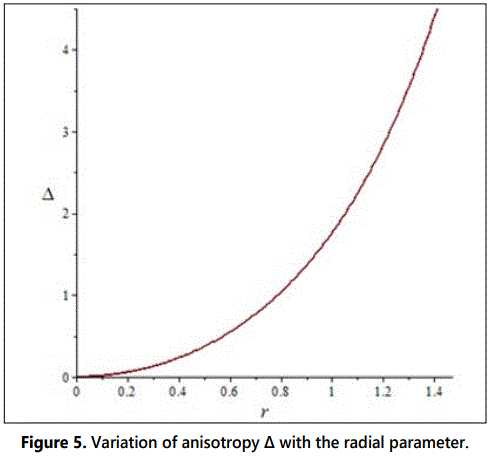
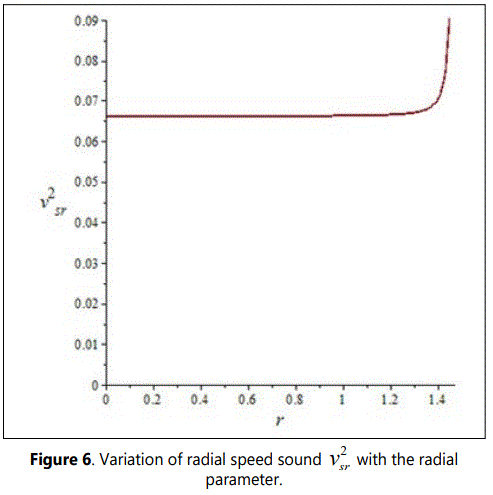
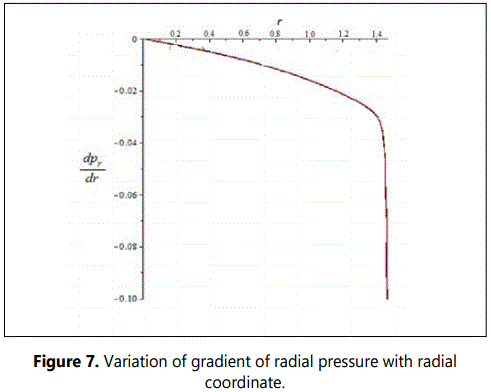
The figure 1 shows that the radial pressure is continuous, finite, decreases radially outward and vanishes at the boundary. In figure 2, we note that the energy density ρ also is finite, continuous and monotonically decreasing function. In figure 3, it is observed that the mass function is regular, strictly increasing and well behaved. Figure 4 shows that the charge density is regular at the centre, non-negative and grows with the radial parameter. In figure 5, the anisotropy factor Δ vanishes at r=0, it monotonically increases and is continuous in the stellar interior reaching a maximum on the surface of the star. In figure 6, we note that the ν²_sr = dp_r/dρ is within the desired range 0 ≤ ν²_sr ≤ 1, which is a physical requirement for the construction of a realistic star [3]. The figures 7 and 8 respectively show that the gradients of radial pressure dp_r/dr and energy density dρ/dr are decreasing throughout the star.

Conclusion

In this paper, we have solved Einstein-Maxwell field equations with a particular form of gravitational potential and a modified Chaplygin equation of state and presented a new class of solution that satisfies the physical requirements of a anisotropic charged stellar model. The radial pressure, energy density, anisotropy, mass function, charge density and all the metric coefficients behave well inside the stellar interior and are free of singularities.

The new obtained solution is expressed in terms of elementary functions which can be useful in the description of compact strange star candidates and the physical study of some kinds of white dwarfs with masses ~0.06 M_sol and r=1.5 Km.

The values of parameters A and B have been chosen in order to maintain the causality condition and the regularity of metric potentials inside the radius of the star. With E²=B=0, the model of Lobo for dark energy stars [59] can be recovered as a particular case of this work and choosing E2≠0, B=0, we can obtain new models with linear equation of state within the framework of MIT-Bag model and generate families of exact solutions for the Einstein-Maxwell field equations for relativistic compact objects and configurations with anisotropic matter distribution. It is to be expected that the stellar models obtained in this research can be used in the description of the internal structure of strange quark stars. The arbitrary constants A, A* B, C, D, E must be well defined in order to reproduce numerical data consistent with super-dense starmodels like neutron star and pulsars.

References

1. Kuhfitting PKF. Some remarks on exact wormhole solutions. Adv Stud Theor Phys. 2011; 5: 365-367.   
2. Bicak J. Einstein equations: exact solutions. Encyclopaedia of Mathematical Physics. 2006; 2: 165-173.   
3. Delgaty MSR, Lake K. Physical Acceptability of Isolated, Static, Spherically Symmetric, Perfect Fluid Solutions of Einsteinʼs Equations. Comput Phys Commun. 1998; 115(2-3): 395-415. doi: 10.1016/S0010-4655(98)00130-1   
4. Joshi PS. Global Aspects in Gravitation and Cosmology. Clarendon Press, Oxford. 1993.   
5. Schwarzschild K. About the gravitational field of a ball made of incompressible liquid according to Einsteinʼs theory. Math Phys Tech. 1916; 424-434.   
6. Tolman RC. Static Solutions of Einsteinʼs Field Equations for Spheres of Fluid. Phys Rev. 1939; 55(4): 364-373. doi: 10.1103/PhysRev.55.364   
7. Oppenheimer JR, Volkoff G. On Massive Neutron Cores. Phys Rev. 1939; 55(4): 374-381. doi: 10.1103/PhysRev.55.374   
8. Chandrasekahr S. The Maximum mass of ideal white dwarfs. Astrophys J. 1931; 74: 81-82. doi: 10.1086/143324   
9. Baade W, Zwicky F. On Super-novae. Proc Nat Acad Sci U S A. 1934; 20(5): 254-259. doi: 10.1073/pnas.20.5.254   
10. Beckenstein JD. Hydrostatic equilibrium and gravitational collapse of relativistic charged fluid balls. Phys Rev D. 1971; 4(8): 2185. doi: 10.1103/PhysRevD.4.2185   
11. Komathiraj K, Maharaj SD. Analytical models for quark stars. Int J Mod Phys. 2007; 16(11): 1803-1811. doi: 10.1142/S0218271807011103   
12. Ivanov BV. Static charged perfect fluid spheres in general relativity. Phys Rev. 2002; 65(10): 104011. doi: 10.1103/PhysRevD.65.104001   
13. Malaver M, Kasmaei HD. Relativistic stellar models with quadratic equation of state. International Journal of Mathematical Modelling & Computations. 2020; 10(2): 111-124. doi: 10.1142/S0218271813500740   
14. Bowers RL, Liang EPT. Anisotropic Spheres in General Relativity. Astrophys J. 1974; 188: 657-665. doi: 10.1086/152760   
15. Gokhroo MK, Mehra AL. Anisotropic Spheres with Variable Energy Density in General Relativity. Gen Relat Grav. 1994; 26(1): 75-84. doi: 10.1007/BF02088210   
16. Esculpi M, Malaver M, Aloma E. A Comparative Analysis of the Adiabatic Stability of Anisotropic Spherically Symmetric solutions in General Relativity. Gen Relat Grav. 2007; 39(5): 633-652. doi: 10.1007/s10714-007-0409-3   
17. Malaver M. Generalized Nonsingular Model for Compact Stars Electrically Charged. World Scientific News. 2018; 92(2): 327-339.   
18. Malaver M. Some new models of anisotropic compact stars with quadratic equation of state. World Scientific News. 2018; 109: 180-194.   
19. Chan R, Herrera L, Santos NO. Dynamical instability in the collapse of anisotropic matter. Class. Quantum Grav. 1992; 9(10): L133.   
20. Malaver M. New Mathematical Models of Compact Stars with Charge Distributions. International Journal of Systems Science and Applied Mathematics. 2017; 2(5): 93-98.   
21. Cosenza M, Herrera L, Esculpi M, Witten L. Evolution of radiating anisotropic spheres in general relativity. Phys Rev D. 1982; 25(10): 2527-2535. doi: 10.1103/PhysRevD.25.2527   
22. Herrera L. Cracking of self-gravitating compact objects. Phys Lett A. 1992; 165(3): 206-210. doi: 10.1016/0375-9601(92)90036-L   
23. Herrera L, Ponce de Leon J. Perfect fluid spheres admitting a oneparameter group of conformal motions. J Math Phys. 1985; 26: 778. doi: 10.1063/1.526567   
24. Herrera L, Nuñez L. Modeling ‘hydrodynamic phase transitions’ in a radiating spherically symmetric distribution of matter. Astrophys J. 1989; 339(1): 339-353. doi: 10.1086/167300   
25. Herrera L, Ruggeri GJ, Witten L. Adiabatic Contraction of Anisotropic Spheres in General Relativity. Astrophys J. 1979; 234: 1094-1099. doi: 10.1086/157592   
26. Herrera L, Jimenez L, Leal L, Ponce de Leon J, Esculpi M, Galina V. Anisotropic fluids and conformal motions in general relativity. J Math Phys. 1984; 25(11): 3274. doi: 10.1063/1.526075   
27. Sokolov AI. Phase transitions in a super fluid neutron liquid. Sov Phys JETP. 1980; 52(4): 575-576.   
28. Usov VV. Electric fields at the quark surface of strange stars in the colorflavor locked phase. Phys Rev D. 2004; 70(6): 067301. doi: 10.1103/PhysRevD.70.067301   
29. Bhar P, Murad MH, Pant N. Relativistic anisotropic stellar models with Tolman VII spacetime. Astrophys Space Sci. 2015; 359: 13. doi: 10.1007/s10509-015-2462-9   
30. Thirukkanesh S, Maharaj SD. Charged anisotropic matter with a linear equation of state. Class Quant Grav. 2008; 25(23): 235001. doi: 10.1088/0264-9381/25/23/235001   
31. Maharaj SD, Sunzu JM, Ray S. Some simple models for quark stars. Eur Phys J Plus. 2014; 129: 3. doi: 10.1140/epjp/i2014-14003-9   
32. Thirukkanesh S, Ragel FC. A class of exact strange quark star model. Pramana - J Phys. 2013; 81(2): 275-286. doi: 10.1007/s12043-013-0582-8   
33. Thirukkanesh S, Ragel FC. Strange star model with Tolmann IV type potential. Astrophys Space Sci. 2014; 352(2): 743-749. doi: 10.1007/s10509-014-1960-5   
34. Feroze T, Siddiqui A. Charged anisotropic matter with quadratic equation of state. Gen Rel Grav. 2011; 43: 1025-1035. doi: 10.1007/s10714-010-1121-2   
35. Feroze T, Siddiqui A. Some Exact Solutions of the Einstein-Maxwell Equations with a Quadratic Equation of State. J Korean Phys Soc. 2014; 65(6): 944-947. doi: 10.3938/jkps.65.944   
36. Sunzu JM, Maharaj SD, Ray S. Quark star model with charged anisotropic matter. Astrophys Space Sci. 2014; 354: 517-524. doi: 10.1007/s10509-014-2131-4   
37. Pant N, Pradhan N, Malaver M. Anisotropic fluid star model in isotropic coordinates. International Journal of Astrophysics and Space Science. 2015; 3(1): 1-5. doi: 10.11648/j.ijass.s.2015030101.11   
38. Malaver M. Strange Quark Star Model with Quadratic Equation of State. Frontiers of Mathematics and Its Applications. 2014; 1(1): 9-15.   
39. Malaver M. Charged anisotropic models in a modified Tolman IV space time. World Scientific News. 2018; 101: 31-43.   
40. Malaver M. Charged stellar model with a prescribed form of metric function y(x) in a Tolman VII space time. World Scientific News. 2018; 108: 41-52.   
41. Malaver M. Classes of relativistic stars with quadratic equation of state. World Scientific News. 2016; 57: 70-80.   
42. Sunzu J, Danford P. New exact models for anisotropic matter with electric field. Pramana – J Phys. 2017; 89(3): 44. doi: 10.1007/s12043-017-1442-8   
43. Komathiraj K, Maharaj SD. Classes of exact Einstein-Maxwell solutions. Gen Rel Grav. 2008; 39(12): 2079-2093. doi: 10.1007/s10714-007-0510-7   
44. Malaver M. Análisis comparativo de algunos modelos analíticos para estrellas de quarks. Revista Integración. 2009; 27(2): 125-133.   
45. Bombaci I. Observational evidence for strange matter in compact objects from the x-ray burster 4U 1820-30. Phys Rev. 1997; 55(3): 1587-1590. doi: 10.1103/PhysRevC.55.1587   
46. Dey M, Bombaci I, Dey J, Ray S, Samanta BC. Strange stars with realistic quark vector interaction and phenomenological density-dependent scalar potential. Phys Lett B. 1998; 438(1): 123-128.   
47. Takisa PM, Maharaj SD. Some charged polytropic models. Gen Rel Grav. 2013; 45: 1951-1969. doi: 10.1007/s10714-013-1570-5   
48. Thirukkanesh S, Ragel FC. Exact anisotropic sphere with polytropic equation of state. Pramana-J Phys. 2012; 78(5): 687-696. doi: 10.1007/s12043-012-0268-7   
49. Malaver M. Analytical model for charged polytropic stars with Van der Waals Modified Equation of State. American Journal of Astronomy and Astrophysics. 2013; 1(4): 37-42. doi: 10.11648/j.ajaa.20130104.11   
50. Bhar P, Murad MH. Relativistic compact anisotropic charged stellar models with Chaplygin equation of state. Astrophys Space Sci. 2016; 361(10): 334. doi: 10.1007/s10509-016-2923-9   
51. Tello-Ortiz F, Malaver M, Rincón A, Gomez-Leyton Y. Relativistic Anisotropic Fluid Spheres Satisfying a Non-Linear Equation of State. Eur Phys J. 2020; 80(5): 371. doi: 10.1140/epjc/s10052-020-7956-0   
52. Caldwell RR, Dave R, Steinhardt PJ. Cosmological Imprint of an Energy Component with General Equation of State. Phys Rev Lett. 1998; 80: 1582-1585. doi: 10.1103/PhysRevLett.80.1582   
53. Xu L, Lu J, Wang Y. Revisiting generalized Chaplygin gas as a unified dark matter and dark energy model. Eur Phys J C. 2012; 72: 1883. doi: 10.1140/epjc/s10052-012-1883-7   
54. Pourhassan B. Viscous modified cosmic chaplygin gas cosmology. Int J Modern Phys D. 2013; 22(9): 1350061. doi: 10.1142/S0218271813500612   
55. Bernardini AE, Bertolami O. Stability of mass varying particle lumps. Phys Rev D. 2009; 80: 123011. doi: 10.1103/PhysRevD.80.123011   
56. Durgapal MC, Bannerji R. New analytical stellar model in general relativity. Phys Rev D. 1983; 27: 328-331. doi: 10.1103/PhysRevD.27.328   
57. Ngubelanga SA, Maharaj SD, Ray S. Compact stars with linear equation of state in isotropic coordinates. Astrophys Space Sci. 2015; 357(1): 40. doi: 10.1007/s10509-015-2280-0   
58. Bibi R, Feroze T, Siddiqui A. Solution of the Einstein-Maxwell Equations with Anisotropic Negative Pressure as a Potential Model of a Dark Energy Star. Can J Phys. 2016; 94(8): 758-762. doi: 10.1139/cjp-2016-0069   
59. Lobo FSN. Stable dark energy stars. Class Quant Grav. 2006; 23: 1525-1541. doi: 10.1088/0264-9381/23/5/006