Research Article
Multi Charged Ions and Mass Spectrometry
Prokhorov GPI RAS, Vavilov str. 38, Moscow, Russia
*Corresponding author: Apollonov VV, Prokhorov GPI RAS, Vavilov str. 38, Moscow, Russia, E-mail: vapollo@kapella.gpi.ru
Received: May 10, 2018 Accepted: May 15, 2018 Published: May 21, 2018
Citation: Apollonov VV, Silnov SM. Multi Charged Ions and Mass Spectrometry. Int J Phys Stud Res. 2018; 1(1): 11-24. doi: 10.18689/ijpsr-1000103
Copyright: © 2018 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Laser mass spectrometry; Microelectronics; Evaporation; Relative sensitivity coefficient; Microelectronics; Plasma plume
Introduction
Laser mass spectrometry is widely used to determine the trace elements and study the distribution of impurities in inorganic and organic materials. The advantages of mass spectrometric methods of elemental analysis, as is known, include: lack of restrictions on the physical form of the sample; ease of sample preparation; needlessness for prior information about the composition of the sample; determination of up to 60 elements in pure substances and up to 40 in the complex natural objects (in the case of simultaneous detection of all isotopes); wide dynamic range; low detection limit, which allows expending extremely small amounts of a sample, i.e., to make use of non-destructive analysis; bulk, local and stratified analysis with high surface (<0.1µm) and depth (3nm) resolution. These advantages favor the widespread use of the method for the analysis of natural objects and technical materials. Besides, more stringent requirements are now imposed on such methods of analysis in order to reduce the detection limits, increase the reproducibility and accuracy of multi charged ions signature analysis [1-5]. Urgent is also the development of non-standard quantitative analysis. One of the problems of mass spectrometry is to identify the factors that govern the relationship between ion compositions in mass spectra and elemental composition of the sample. In this connection, much has been made to understand the processes occurring during the formation of ions from the particles a solid body. On this basis, work is underway to elaborate non-standard analysis techniques. Successful implementation of the methods should be based on theoretical and experimental studies of the mechanisms of ion formation, the relationship of the intensity of the ion currents with the concentrations of elements determined, their parameters, the composition and the basic properties of the matrix, and the conditions of the impact on the sample in the ion source. One of the main goals of the theory as applied to the elemental mass spectrometric analysis is to provide a method for calculating the relative sensitivity coefficients.
As seen in many sources, significant theoretical and experimental results have already been obtained in the field of laser mass spectrometry. However, the relative yield of ions of different elements is studied mainly for the case of simple substances (three component materials at best). The theoretical research in this area is extremely difficult due to non-equilibrium processes, spatial in homogeneity of the plasma source, changes in its parameters during the target irradiation and plasma expansion. One can offer an approximate description of the processes leading to the formation of the mass spectrum. It is based on the representation of the process in two stages, each of which is assumed independent and successive:
1. Material atomization, ionization of atoms, and expansion of plasma;
2. Formation of an ion beam, mass analysis, and detection of ions.
The main idea here is that at each stage the behavior of atoms of different elements is determined by one of the main parameters characterizing these elements. This greatly simplifies the description of all the main processes. In this approach, the relative sensitivity coefficient can be represented as the product of the relative yield of ions and the instrumental factor. The relative yield of ions characterizes the discrimination of atoms of different elements in the first three stages of the formation of a mass spectrum, which are associated with the plasma processes. The instrumental factor takes into account the discrimination of ion composition, which is related to the final stages of the formation of the mass spectrum [6].
In laser mass spectrometry, in considering the first stage most applicable is a quasi-equilibrium model [7]. Let us clarify the physical meaning of model temperatures: They characterize the degree of non-equilibrium processes under consideration. The higher the atomization temperature, the faster and more unbalanced the evaporation; the higher the ionization temperature, the stronger the effect of the nonequilibrium recombination process in the expansion of the plasma [8, 9]. From the analytical viewpoint, the higher the model temperatures, the smaller the difference between the final ionization degree of atoms of different elements, despite the difference in their physical properties. In the limit, when the values of both temperatures tend to infinity, the coefficients of the relative yield of ions are close to unity. This means that discrimination in the stages of atomization, ionization and recombination are completely excluded, i.e., the ion composition of the plasma after its expansion is equivalent to the atomic composition of the sample. Thus, the previously proposed models, according to which the coefficients of the relative yield of ions under certain conditions is equal to unity in the laser mass spectrometry [10], are special cases of the quasi-equilibrium model (provided that the instrumental factor is the same for different elements).
The instrumental factor is found using the calibration with respect to pure elements or by statistically processing the results of a large number of analyzes of standard samples.
Statistical processing of the results of the experiments and the available set of literature data has shown that the quasi-equilibrium model allows one to interpret the relative sensitivity coefficients more accurately than any empirical formulas [11]. The main advantage of the proposed model is that it allows one to judge the nature of the processes occurring during the formation of ions, and the main reasons for the deviation of the ion current composition on the elemental composition of the sample. Naturally, the quasiequilibrium approach is necessary only to simplify the calculations of the relative sensitivity coefficients and in any case does not replace the physical processes that occur during the formation of a plasma torch.
Research in this area offers ways to stabilize the conditions of formation of ions by controlling the irradiation parameters of a sample in the source. This improves the reproducibility and accuracy of analysis results using both standard and non-standard analysis of the sample compositions. Control of the mass spectrum composition (compared to singly charged, multiply charged and complex ions) should lead to a significant reduction of influence of overlapping and thus to a decrease in the detection limits in concentrations of many elements. A further decrease in the detection limits in mass can be achieved by increasing the residual ionization degree of atoms and by decreasing the spread of ions in energy.
Laser ion source for mass spectrometer
Laser ion sources for mass spectrometric analysis of solids can be divided into two main types according to the purpose for which the laser is used: either as an evaporator for sampling, or for producing a dense high-temperature laser plasma, which is an emitter of ions. The first type of the laser source and analytical capabilities of combining a laser (free-running regime) and a mass spectrometer were studied by many authors. Although the characteristic dimensions of the structural elements of laser sources in these cases vary somewhat, the principle of their action is the same, and the main parameters are close. For the second type of ion sources a dense high-temperature plasma, which is an emitter of ions, is produced during laser irradiation.
One of the simplest designs of a laser ion source of second type–a time-of-flight mass spectrometer–was proposed and developed by scientific group of Yu.A. Bykovskii [10]. The source had a target irradiated with a laser, a uniform electric field produced by the flat grid and a target, where the generated ion beam is accelerated. Such a source design with a uniform electric field to accelerate ions in a time-of-flight mass spectrometer with an electrostatic analyzer was investigated in detail by these authors. A laser ion source for time-of-flight mass spectrometry with an electrostatic analyzer using a single-potential lens was considered in [12]. If the laser beam is incident on the sample surface (thin film) from the side which is opposite to the analyzer, the range of the samples to be analyzed is very limited. Nevertheless, this source design is used in a LAMMA-500 laser mass spectrometer Liebold-Heraues (Germany). Given the advantages and disadvantages of the previous sources, a design was proposed, which makes use of a set of apertures to reduce the region of the laser-plasma plume from which the ions enter the accelerating gap of a pre-injectors for subsequent transport to the electrostatic mass analyzer. To eliminate the effect of the backward expansion and possible breakdowns, and thus to change the accelerating voltage, a closed cycle expander was used to extract ions in an electrostatic ion mass analyzer. Consequently, the laser plasma ions arrive into the accelerating gap of the pre-injector only from the region bounded by the system aperture. In the ion beam extraction system use was made of a scheme fixing the boundary with the help of a flat fine-grained grid.
Temporal and mass resolution of the devices with an electrostatic analyzer
The operation principle of mass spectrometric systems is based on the separation of ions with different ratio of their mass to charge (m/z). Regardless of all the principle of separation of ions, mass spectrometric systems consist of three main components: an ion analyzer, which is used to separate ions according to their ratio m/z; a detector, which permits receiving extracted ions; and a recording device, which retrieves information. The main parameters of a mass spectrometer are the resolution and light intensity. The resolution of a mass spectrometer is determined by its ability to separate ions with different masses. This value is usually expressed in relative units Rm=M/▲M, where ▲M=m1-m2 is minimum difference of ion masses, detected separately. The light intensity of a mass spectrometer in general is the ratio of the number of ions, which have reached a detecting device, to the total number of ions produced in the ion source. Thus, the light intensity of a mass spectrometer is characterized by the transmission coefficient of the ion beam through the analytical part of the mass spectrometer.
In order to improve the main characteristics of mass spectrometric devices, a special field is created in the analyzer, which is focused with respect to energy and direction. The sensitivity of a mass spectrometric device relies on a combination of characteristics of the ion source, analyzer, and detection system. First, the sensitivity of the analysis depends on the amount of a substance (in grams) required to detect a certain element of interest in this substance. Second, the sensitivity can correspond to the minimum relative concentration of the detected impurity element. This characteristic is called the relative detection limit. Both these characteristics are determined by a set of parameters of the ion source, analyzer, and detecting device as well as by the object to be analyzed, background noise in the device, etc.
To obtain a sufficiently high resolution, a time-of-flight analyzer (EMAL-1) utilizes an axially symmetric field whose ion-optical characteristics are calculated using the theory developed in [13].
When the object surface is irradiated by a Q-switched laser, the time of emission of laser plasma ions is determined by collisional processes that take place after the end of the laser action. The mean free path of ions depends on their energy and plasma density. During expansion the density decreases and there comes a time when the mean free path of the ion at a given energy exceeds the size of the plasmoid. The emission time depends on the ion energy and decreases faster than 1/E0.5. For example, for tungsten ions with an energy of 100eV, the emission time is equal to or less than 250ns. The emission region from which ions are detected, increases with the detection threshold. The resolution should drop down a level from which the pulse width is measured.
In the energy range of 50–500eV, the number of ions is approximately the same; in addition, in the analytical part of the mass spectrometer, all the ions have approximately the same energy E=Eo+U, where U is accelerating voltage of a pre-injector, because U»Eo, and as shown in paper [9] the maximum resolution that can be obtained in EMAL-1 devices is 400–500. It should be noted that when a pre-injector with an accelerating voltage Uy=1.5kV is used, the energy range of the ions detected during one laser shot is very small. Thus, the desire to increase the resolution of the device leads to an increased uncertainty in the determination of the concentration of elements. This is due to the fact that the energy transmission of the mass spectrometer is less than the energy spectrum of ions of different elements. Figure 1 shows the signal measured by EMAL-1 for lead.
Limiting concentration sensitivity
The time-of-flight and electrostatic analyzer can be viewed as a system, which forms the ion beam. The flux density in the beam must not exceed a certain critical density of the ion current [14] for the heaviest masses. In the case of a laser ion source there are a number of additional functions performed by the analyzer. First, use is made of a pre-injector which separates the electrons and ions of the plasma and converts the pulse plasma flux into the ion current pulses. Second, the analyzer selects only a certain interval from the full energy spectrum of the plasma determined by time, and hence by the mass resolution of the device.
The emission region decreases with increasing laser plasma ion energy. Thus, by decreasing object slit (by stopping or reducing the slits S1 and S2), we artificially introduce discrimination for low-energy ions, and therefore the energy spectra of the laser torch, obtained by means of such devices differ from the energy distribution during the free expansion of the plasmoid.
The absolute sensitivity of the device is obviously related to the detector sensitivity and the ion loss factor in the formation of the ion beam. As a detector EMAL-1 utilizes secondary electron multipliers SEM-1 and SEM-2, which allow detecting individual ions and have a time resolution better than At>20ns. However, this sensitivity is not statistically justified, since in this case the error amounts to 100%. Thus, we can assume at least 10–100 ions detected by the SEM to be the limiting value of the absolute sensitivity; in this case, the higher the accuracy of the concentration determination, the lower the sensitivity or the higher the statistics. If Emax-Emin=1000eV, the absolute sensitivity is 10-12g. This indicates that for EMAL-1, when the sampling of the analyte is realized by single laser shots, it is possible to achieve high absolute sensitivity of the analysis, and the concentration sensitivity is determined by the resolution of EMAL-1. Figure 2 shows the dependence on the concentration sensitivity on the mass resolution for ion energies E=400eV. Figure 3 presents the dependence of the limiting resolution on the energy of singly charged ions. Figure 4 and Figure 5 show typical oscillograms of singly charged ions for different alloys. The main features of such devices, directly related to the concentration sensitivity and mass resolution, are: high mass resolution is limited primarily by two parameters–the size of the ion emission region (or the time of emission) and temporal resolution of a particle detector. The concentration sensitivity is unambiguously related with a dynamic operation range of a SEM, broadband amplifier, and oscilloscope. Thus, a correct quantitative analysis can be performed at the level of no more than 0.01%. For semi-quantitative analysis the concentration sensitivity range can be increased. When detecting the ions in individual acts of laser interaction with the analysis, the limiting concentration sensitivity is 10-4%. The concentration sensitivity and mass resolution increase with the use of higher energy ions.
Thus, to achieve a high sensitivity concentration and high mass resolution requires an elemental analysis at a radiation flux density of 2×109W/cm2 in the range of ion energies of 300–400eV
Express method for quantitative analysis of alloys
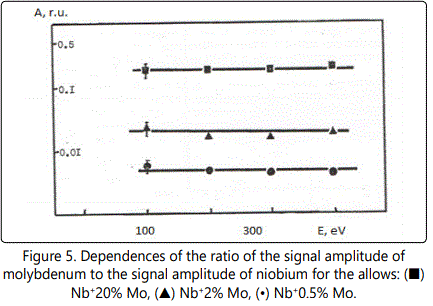
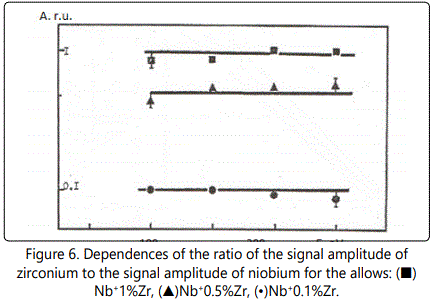
In time-of-flight systems, as a rule, power transmission of the device is substantially less than the width of the energy spectrum of the ions of the laser plasma torch. Since the energy spectra of the ions of different elements in the region of high energies are, in general, different, the detection of the ions in a narrow energy range leads to errors during the elemental analysis of materials. Figures 1–6 show the amplitudes dependences of the signals and the relative yield of niobium-based alloys. For ‘pure’ niobium the maximum energy distribution of singly charged ions corresponds to the energy of 100eV, whereas for tungsten alloys the maximum energy distribution of tungsten shifts to higher energies and is equal to 150eV. In this case, the power transmission of the mass spectrometer was about 2eV. Figure 5 and Figure 6 show the relative yield of singly charged ions as a function of the detection energy for the two alloys. These graphs clearly explain the errors arising in determining the concentration of elements, if the power transmission of the mass spectrometer is much less than the energy spectrum of the ions. For alloys we failed to observe the differences in the energy distributions of singly charged ions. Figures 5 and 6 show the dependences of the relative yield of singly charged ions on the detection energy for three concentrations of molybdenum (20%, 2% and 0.5%) and zirconium (1%, 0.5% and 0.1%).
Thus, for express analysis of complex niobium alloys with a concentration of carbon (0.1%–0.5%), molybdenum (2%–5%), zirconium (0.5%–1.5%), tungsten (5%–15%), such devices should mass resolution of at least 50 on a level of 0.0005 (Figures 4, 5), the accuracy of determination of the concentration being at least 10%.
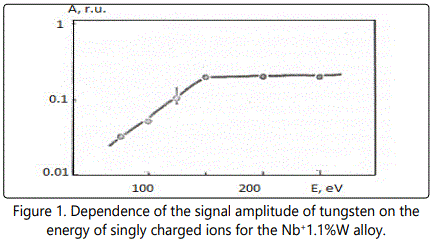
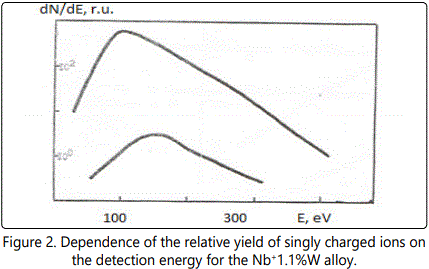
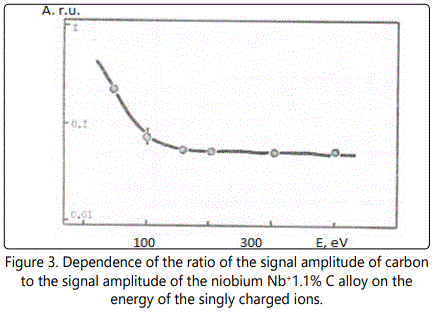
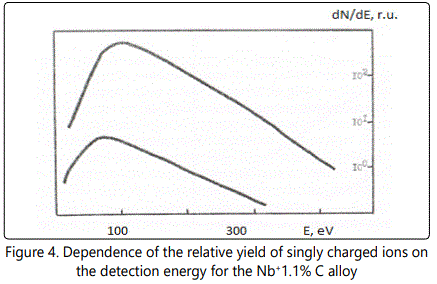
In these alloys, carbon and tungsten were detected by the amplitudes of the ion signals of recombination energy distributions. For quantitative analysis of the samples’ composition, this method requires a high stability for the following parameters:
- flux density of the laser radiation, i.e., the laser energy and the size of the focal spot;
- accelerating voltage of the pre-injector and the bias voltage on the plates of a spherical capacitor;
- deviation of the center of the focal spot of laser radiation from the axis of the mass spectrometer path should not be significant (10% of the size of the focal spot).
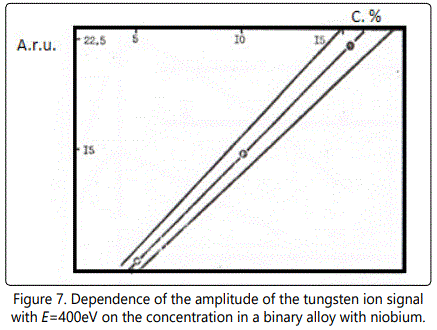
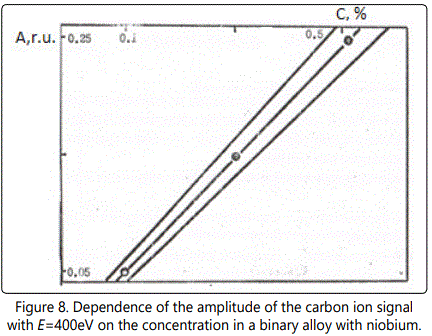
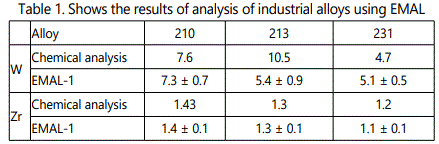
Calibration curves (Figures 7–8) at 6×109W/cm2 and the diameter of the focal spot of~100µm for different concentrations of tungsten and carbon are presented for the ion energy of 400eV. The concentration of carbon and tungsten is determined with an accuracy of better than 10%. Table 1 shows the results of analysis of industrial alloys using EMAL-1 and compares them with the results of chemical analysis.
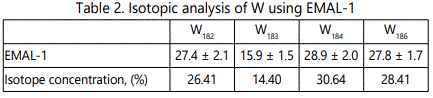
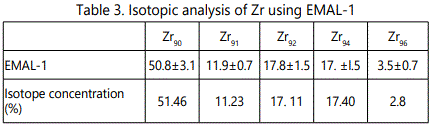
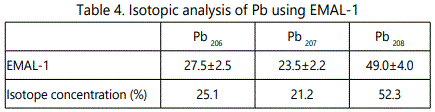
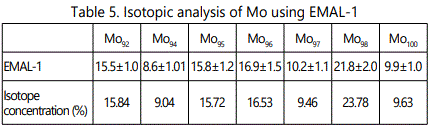
EMAL-1 was used for isotopic analysis of Zr, Mo, W, Pb in the alloys with niobium and pure materials. As seen from Tables 2–5 relative error does not exceed 10%, except zirconium (20%), when the isotope concentration differ significantly.
These studies made it possible to improve the ion source for mass spectrometry by taking into account the features of ion emission from a laser-plasma torch; therefore, the following characteristics were obtained:
- mass resolution at half-height of ion peaks was at least
400;
- mass resolution at a level of 0.0005 of ion peaks was at least 50;
- stability of the arrival time of the ion in the SEM was at least their half-widths;
- relative concentration sensitivity at a mass resolution of
50 was better than 0.01%.
Problems of quantitative analysis of laser mass spectra
Quantitative analysis using laser mass spectrometry is an urgent task. Improving reproducibility of the results is achieved by stabilizing the conditions of ion formation in the source and by automating the processing of mass spectra. However, only random errors are reduced in this case. The problem of reducing systematic errors or their correct identification is still relevant.
Usually this problem is solved by introducing the relative sensitivity coefficients of the elements. The relative sensitivity coefficients of different elements change over a wide range (up to the order of magnitude) in different experiments [1-11]. The reason probably lies in the fact that these coefficients often include discriminations of ions of different elements both in the formation of a plasmoid, and during transportation of the ion beam to a mass spectrometer. Purely physical factors influencing the formation of relative sensitivity coefficients for different elements are considered in this paper. Systematic errors arising due to instrumental factors are related to the influence of the scattered magnetic field and the space charge of the beam. Despite the fact that the reasons of the discrimination in the ion mass and charge of the mass analyzer, assembled under the Mattauch-Herzog scheme, are known, the ways of proper account of these factors are not considered in the literature.
The authors of paper [12] consider the influence of the refractive index of the ion beam at the boundary of the electric field on the width and shape of the analytical lines. This effect can be taken into account, for example, by integrating the line during photometry [8]. In paper [15] the correction for the scattered magnetic field is not accurate enough because of the uncertain degree of interaction of the beams of different masses and structural imperfections in the assembly of the analytical device. The data of paper [16] make it impossible to determine the systematic error in the absence of standard compositions, which are similar in composition to the sample. This is probably due to the fact that these papers focus on the physical side of the problem, with the analytical part being poorly developed. The problem of achieving the best accuracy and maximum sensitivity of the analysis should be solved by careful consideration of all systematic errors, with optimization of parameters of incident radiation and ion-optical system. In addition, investigation of the processes of production of new elements by the obtained mass spectra is possible only in case of a complete separation of the physical and instrumental factors in determining the relative sensitivity coefficients of the elements. This is the reason to consider instrumental errors as components of errors arising during calibration.
Estimate of the quality of analytical lines
A necessary condition for quantitative analysis on the devices with double-focusing (EMAL-2) is the absence of defects in the analytical lines of the mass spectrum, which arise due to ion-beam optical aberrations during its transport. In general, this is achieved by using the methods of adjusting the analytical system of the instrument [9]: the mass spectrometer was calibrated for a set of pure elements C, Si, Fe, Ge, Sn, Yb, and Pb by measuring the dependence of the photo emulsion sensitivity on the ion mass. The emulsion contrast was determined by measuring the isotopes of tin.
The quality of the analytical lines was assessed visually by the mass spectrum of a standard sample (Br669). Analytical lines used for photometry should have a strict rectangular shape, uniform intensity in height and approximately Gaussian distribution in width. After the analytical lines that satisfy the above conditions are obtained, it is necessary to optimize the parameters of the ion-optical system. The relative sensitivity coefficient is an integral parameter that takes into account the differences in the relative yield of ions of elements from laser plasma and the discrimination of ions during their transport to the mass analyzer. Using the conventional method of calibration, i.e., the dependence of the photo-emulsion sensitivity on the ion mass, the obtained values of the relative sensitivity coefficients implicitly contain coefficients K. Since K values are determined by the masses of elements, their contribution to the relative sensitivity coefficients may be the cause of the general dependence of these coefficients on the mass. Thus, the use of the refined calibration characteristics allows one to consider the obtained values of the relative sensitivity coefficient as the values characterizing the relative contribution of ions of different elements of a plasmoid. To increase the light intensity of the mass spectrometer, it is needed to optimally combine the conditions of laser irradiation of the sample, the parameters of the ion beam formation system and the parameters of the mass analyzer.
Expansion of ion beams due to the own charge and disordered spread in transverse thermal velocities during their transport between the object and the aperture slits separated by a distance equal to L, on the one hand, and the finite size of the slits, on the other hand, determine the existence of possible discriminations in the ion masses at the edges.
The absence of significant discrimination in the mass analysis because of the action of the space charge of the ion beam during its formation and transport (for the given parameters of the ion-optical system: 0.05mm<d<0.6mm and 2×109W/cm2) is considered optimal for the most efficient ionization of atoms of trace elements in order to achieve the best accuracy and maximum sensitivity. Discriminations related to the scattered magnetic field and space charge are independent; therefore, to achieve maximal sensitivity, while maintaining the best accuracy of the results, it is needed in a reasonable manner to minimize the combined influence of these effects. To this end, the size of the object slit S is optimized. On the one hand, the increase in S to a value greater than the optimal value increases the number of ions necessary for the emergence of the analytical line and its broadening. On the other hand, reducing S below the optimal value significantly increases the exposure time needed for the emergence of the required analytical line. Accounting for the instrumental factor in the construction of the calibration curve allow one to consider the obtained values of the relative sensitivity coefficient as parameters characterizing the relative yield of ions of different elements from a plasmoid. To ensure the maximum sensitivity in the analysis of samples of different composition use, advantage is taken of the position of the object slit corresponding to the maximum ion current of the irradiated sample. In order to achieve the lowest detection limits of trace element contents, the size of the object slit is optimized.
Relative sensitivity coefficient dependence from the starting conditions analysis.
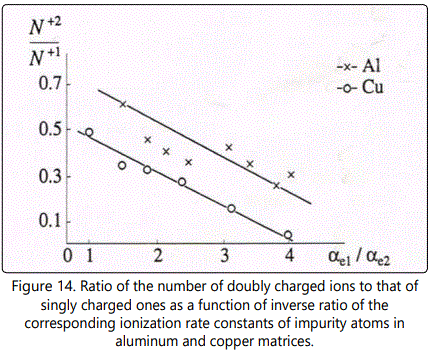
Recent years have been marked by a substantial reduction in the number of publications on sample composition analysis using laser mass-spectrometry. This is due to the fact that available mass-spectrometers with laser ionization do not fit some of the requirements of practical analysis [18-19]. The problem of validity of the results is of value not only in the case of a laser excitation source. This problem is connected with determination of relative sensitivity coefficients (RSC) for various impurities. It was shown in [17-20] that parameters of exciting radiation such as fluence q and spot diameter d influence the value of RSC of impurities in a copper matrix. The authors of [24-25] proposed an a priori approach to calculate RSC. However, variation of the matrix mass when analyzing other samples is expected to result in variation of main parameters of the plasma plume (for example, lifetime T0 [26]) and relative yield of ions of different impurities from laser-produced plasma. Such a “matrix effect” was reported by several authors [27,28]. The influence of the matrix mass on the energy spectrum and relative yield of ions of main components of the plasma plume was studied in detail in Refs. [26-29]. However, the behavior of the impurity component was not studied in the above papers.
We report here on experimental studies of the influence of the matrix component of a plasma plume on ionization efficiency of impurity atoms, processes of acceleration and recombination of impurity ions in laser-produced plasma. This work is a continuation of a series of experiments on studies of recombination processes in multi-component laser plasma published in [24].
Experiments were made with a mass-spectrometer EMAL-2 [26] using a pulsed Nd: YAG laser with a repetition rate of 50Hz operated in the regime of minimal longtime instability of the output power [30-31]. The analytical part of the masss-pectrometer was calibrated according to recommendations of [32] to ensure proper accounting for the influence of the instrumental factor on the mass discrimination of ions along the flight path in the mass-spectrometer. The target material was a standard Al-Si-45 compound containing impurity elements (Si, Ti, Cr, Mn, Fe, Cu, Zn, As, Sn, Sb, Pb) at concentrations ranging from 1 to 10-4at%. Experimental data were processed using the method described in [25, 33]. Experimentally, we studied the yield of impurity ions per unit illuminated area N+z/ S as a function of laser spot diameter d ranging from 0.05mm to 1mm, at fixed values of q=2x108 and 8x109Wcm-2.
Influence of plasma torch initial size and matrix contents on the impurities analysis result.
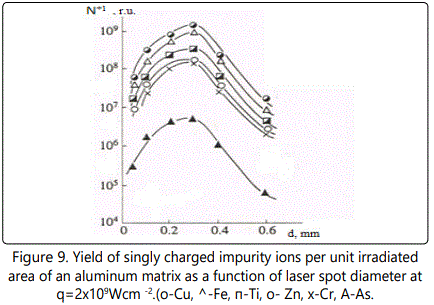
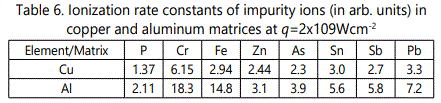
The yield of singly charged impurity ions as a function of the laser spot diameter at q=2x109Wcm-2 is shown in Figure 9 The dependence N+z/ S is similar for all impurity ions: this function rapidly grows as d increases from 0.05 to 0.3mm; in doing so at d>0.2mm the function slope with respect to the abscissa becomes more gradual; at d=0.3mm the function attains its maximum and starts to decrease steadily with further increase in d.
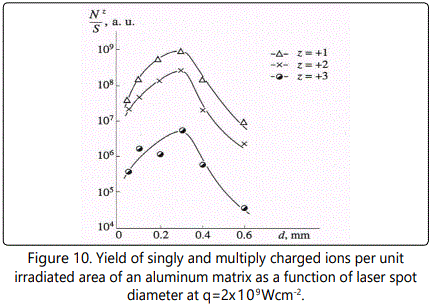
The yield of iron ions with z ranging from 1 to 4 as a function of d at
q=2x109Wcm-2 is shown in Figure 10.
The function N+z/ S for z=+1 - +3 attains the maxi mum at d =0.3mm, and for z=+4 it has the maximum value at d=0.4mm. From these profiles one can conclude that the rate of increase of the number of ions with the increase of d becomes lower at larger z, while the rate of decrease (the slope of the right side of the curves in Figure 10) becomes higher at larger z. Such dynamics of the charge spectra with variation of d are typical of all impurity ions.
Let us compare the yield of impurity ions from samples with copper and aluminum matrices. The yield of singly charged iron ions per unit illuminated area as a function of laser spot diameter for A1 and Cu matrices at q=2x109Wcm-2 is shown in Figure 11 Comparing the dependencies NFe+/ S on d one concludes that in the N+z/ S case of A1 matrix, the maximum of the function lies at larger d (0.3mm) than in the case of the Cu matrix (d=0.2mm). The slope of the left side of the curveis N+z/ S larger for the A1 matrix. The rate of decrease of the function N+z/ S is also higher for iron ions in the aluminum matrix. Note also that these distinctions are typical of all impurity ions.
Thus, the function N+z/ S behaves similarly for all impurity ions both in copper [24] and aluminum matrices. In doing so in the case of impurities in the aluminum matrix the function N+z/ S attains its maximum at larger spot diameters, and the rate of increase of the number of ions with increase in d is larger. The question arises of why the maximum of the function N+z/ S shifts for the same ions? It was shown earlier that me maximum of this function is governed by the competing processes of ionization and recombination and can be determined from a simple relation
τi(z, A) ~ τ0(z, A) ~ τr(z, A). For the same impurity we have τ0A](z, A) ≈τ0Cu(z, A), where the lifetime τ0 can be expressed as τ0~d/v. If one assumes that v is the local sound velocity then v~A-0.5 τ0~dA0.5. Consequently, we have 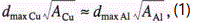
In remarkable accord with the experimentally observed shift of the maximum from 0.2mm to 0.3mm.
From this analysis one concludes that the relation τ0~dA0.5 can be used for a priori calculation of impurity yield.
Influence of matrix on ionization efficiency of impurities
It was shown in Refs. [15, 26, 34] that the left branch of the dependence τ0~dA0.5 is governed predominantly by the processes of ionization, while the right branch of the dependence is governed by the processes of recombination in a plume; in doing so the efficiency of both processes increases at larger d. The maximum of the dependence is determined to a certain degree by competition of the processes of ionization and recombination.
Let us compare ionization of impurity atoms in copper and aluminum matrices. The ratio of the number of ions formed at the maximum of the function N+z/ S to that formed at d =0.05mm and q=2x109 Wcnr2 in these two matrices is given in Table 6. It is seen that efficiency of ionization characterized by the growth rate of the function N+z/ S is higher for impurities in the aluminum matrix compared to that in the copper one. This fact is also clearly seen in Figure 11. The observed dependence can be explained as follows. Taking into account the fact that during plume expansion, ions of the matrix and impurity behave similarly, one can suppose that the difference in ionization efficiency is due to characteristics of the plasma plume determined by the matrix (the target excitation conditions are assumed to be the same). The lifetime τ0 governed by the matrix component [26] has little influence on efficiency of ionization processes because we neglect the recombination process in the plume at d<dopt. On the other hand, ionization of impurity elements is governed by Ref. [35]

where na, ni, ne are the densities of atoms, ions and electrons, respectively. Considering the fact that the quantity αe ne is the probability of two-particle collisions per unit time we see that increased ionization efficiency in the aluminum matrix compared to the copper one is either due to larger value of ne, or due to higher Tt. In doing so the values ne and Tt are coupled to each other, but increase of Tt results in increase of probability of electron collision with an atom, while increase of αe results in increase of ne for the corresponding impurity element because according to Eq. [16]

Coupling of ne with Te can be traced as follows. It was shown in [8] that for copper matrix

where the coefficient at q is a function of plasma density δ and mass of the matrix component M [17]. Assuming δ = ne we have

Consequently, the increase of the ionization rate of impurity atoms in the aluminum matrix compared to the copper one (provided q is constant) can be explained as follows. In the aluminum matrix the ionization potential of the matrix component ϕM is higher, resulting in increased ionization rate of the matrix atoms αeM, in accordance with Eq. (3). The matrix atoms are ionized both by the laser field and by electron impact. They are the main source of electrons in plasma. Consequently, increase of the ionization rate of the matrix atoms results in increase of electronic density ne and energy, in accordance with relation (5) and the relation

Here dni/dt was replaced by dne/dt, in compliance with assumptions made above. In turn, the ionization rate of atoms of a fixed impurity is determined by the increase of electronic energy according to relation (3), and the value of dni/dt is determined by ne, in accordance with Eq. (2). It should be noted that the question as to which quantity, ne or Te, governs the increase of αe, remains unanswered. Solution of this problem is rather difficult because the quantities ne and Te are closely coupled to each other, and Eq. (5) describes this coupling only approximately.
Acceleration and recombination of impurity ions in presence of different matrix components of the plasma plume
Plasma plume expansion is accompanied by ion acceleration due to pressure gradient and presence of an electric double layer determined by areas with non-compensated charge [33-35]. The process of multi-component plasma expansion is determined by the matrix component [24]. The acceleration efficiency of matrix and impurity ions is proportional to the ratio of the ion charge to its mass [34]. It was shown that recombination complicates consideration of ion acceleration, because accelerated ions gain additional velocity with respect to neutral particles of the plasma plume, thus increasing probability of recharging.
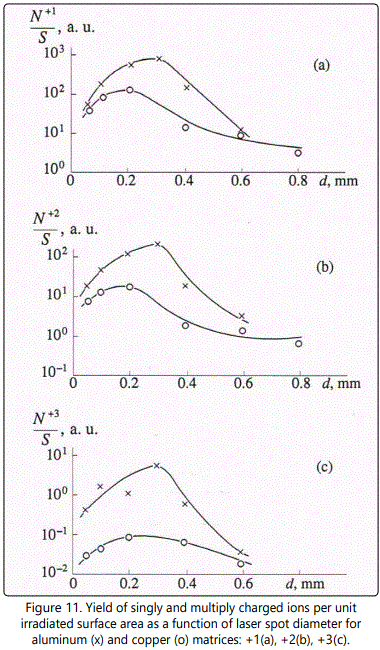
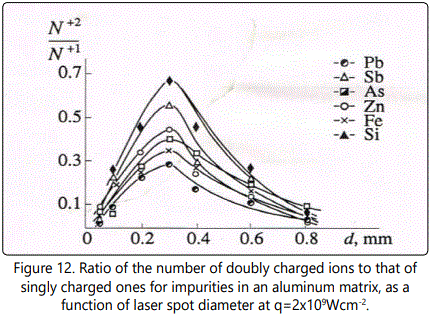
We will describe ion acceleration in a plasma plume in terms of charge ratios of ions during expansion, as was done above. The ratio of the number of doubly charged ions to the number of singly charged ones as a function of laser spot diameter d at q=2x109Wcm-2 is shown in Figure 12 and Figure 13 for aluminum and copper matrices, respectively. A characteristic feature of the
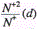 dependencies
dependencies 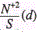 is the maximum at d=0.3mm, the height of the latter increasing with the increase of ion mass. Similar increase of the ratio
is the maximum at d=0.3mm, the height of the latter increasing with the increase of ion mass. Similar increase of the ratio 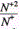 at the maximum with increase of M is also observed for ions in a copper matrix, though the maximum shifts to smaller values of the spot diameter d with increase of M. For example, for Zn and As the maximum value of the ratio
at the maximum with increase of M is also observed for ions in a copper matrix, though the maximum shifts to smaller values of the spot diameter d with increase of M. For example, for Zn and As the maximum value of the ratio 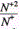 is achieved at d=0.6mm, for Sn - at d=0.4mm, and for Pb the maximum is achieved at d=0.2mm. Such difference of the plots can be attributed to the fact that the mass of aluminum is essentially smaller than that of all impurities. As a result, the maximum of the ratio
is achieved at d=0.6mm, for Sn - at d=0.4mm, and for Pb the maximum is achieved at d=0.2mm. Such difference of the plots can be attributed to the fact that the mass of aluminum is essentially smaller than that of all impurities. As a result, the maximum of the ratio 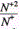 is achieved at the optimal value of the laser spot diameter from the point of view of the maximum yield of singly and doubly charged ions. Moreover, a larger value of ne for aluminum plasma (as was pointed out above) results in more effective ion acceleration. In the case of the copper matrix, masses of copper and a majority of impurities are close, and the maximum of the ratio
is achieved at the optimal value of the laser spot diameter from the point of view of the maximum yield of singly and doubly charged ions. Moreover, a larger value of ne for aluminum plasma (as was pointed out above) results in more effective ion acceleration. In the case of the copper matrix, masses of copper and a majority of impurities are close, and the maximum of the ratio 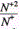 only shifts towards dopt (d=0.2 mm). This behavior is clearly seen for Sn and Pb ions having masses considerably different from that of copper. Obviously, with increase of ne
in a copper plasma the maxima of the ratio
only shifts towards dopt (d=0.2 mm). This behavior is clearly seen for Sn and Pb ions having masses considerably different from that of copper. Obviously, with increase of ne
in a copper plasma the maxima of the ratio 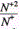 for all impurities will tend to dopt =0.2mm.
for all impurities will tend to dopt =0.2mm.
It should be noted that differences in dependencies for copper and aluminum matrices are not connected with the peculiarities of ionization processes. This conclusion is illustrated by Figure 14 which shows the ratio of the number of doubly charged ions to that of singly charged ones as a function of inverse ratio of the corresponding ionization rate constants αe1/αe2 of impurity atoms in copper and aluminum at q=8x108Wcm-2. The value 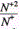 decreases with increase of the ratio αe1/αe2 with the same rate in copper and aluminum. Larger absolute values
decreases with increase of the ratio αe1/αe2 with the same rate in copper and aluminum. Larger absolute values 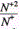 of in aluminum plasma can be attributed to more effective processes of ionization, in particular due to shift of dmix (z=1) to larger values (dmax=0.3mm).
of in aluminum plasma can be attributed to more effective processes of ionization, in particular due to shift of dmix (z=1) to larger values (dmax=0.3mm).
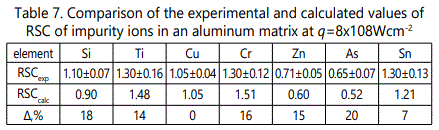
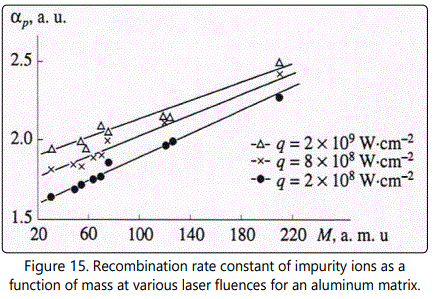
It was pointed out above that the right branch of the function 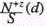 is governed by dominating processes of recombination. Let us determine the recombination rate constant αp similar to αe, namely from the rate of decrease of brightness as d increases. The experimental data on recombination rate constants of singly charged ions as functions of their mass at various values of q are shown in Figure 15 It is seen that αp increases with increase of M from 1.8 for P to 2.3 for Pb at q=8x108Wcm-2. In doing so the character of the dependence of αp on M does not change and remains linear: αp~M. As q increases from 2x108 to 2x109Wcm-2, αp increases for all impurities though this increase is not significant and amounts to less than 30%. This circumstance can be attributed to the fact that increase of q results in increase of the number of “cold” electrons and consequently in increased efficiency of recombination processes in the plasma plume. Additionally this simultaneously raises the yield of doubly charged ions. As these ions recombine, they contribute to the singly charged plasma component. Consequently, the variation of αp with increase of q is not so considerable as one might expect from consideration of the influence of Ne only at the stage of ion recombination. It was shown in [20] that in the process of copper plasma expansion αp does not depend on M for fixed z. Strong correlation between the recombination rate constant and ion mass of the corresponding impurity in aluminum is due to variation of the plasma plume parameters. Increase of ne results in more effective recombination as is seen in Figure 11 in the case of singly charged ions of iron in copper and aluminum. Variation of τ τ0 in accordance with Eq. (1) results in increase of αp for impurity ions with a mass larger than that of the matrix component. This is due to faster expansion of aluminum plasma compared to the copper plasma.
is governed by dominating processes of recombination. Let us determine the recombination rate constant αp similar to αe, namely from the rate of decrease of brightness as d increases. The experimental data on recombination rate constants of singly charged ions as functions of their mass at various values of q are shown in Figure 15 It is seen that αp increases with increase of M from 1.8 for P to 2.3 for Pb at q=8x108Wcm-2. In doing so the character of the dependence of αp on M does not change and remains linear: αp~M. As q increases from 2x108 to 2x109Wcm-2, αp increases for all impurities though this increase is not significant and amounts to less than 30%. This circumstance can be attributed to the fact that increase of q results in increase of the number of “cold” electrons and consequently in increased efficiency of recombination processes in the plasma plume. Additionally this simultaneously raises the yield of doubly charged ions. As these ions recombine, they contribute to the singly charged plasma component. Consequently, the variation of αp with increase of q is not so considerable as one might expect from consideration of the influence of Ne only at the stage of ion recombination. It was shown in [20] that in the process of copper plasma expansion αp does not depend on M for fixed z. Strong correlation between the recombination rate constant and ion mass of the corresponding impurity in aluminum is due to variation of the plasma plume parameters. Increase of ne results in more effective recombination as is seen in Figure 11 in the case of singly charged ions of iron in copper and aluminum. Variation of τ τ0 in accordance with Eq. (1) results in increase of αp for impurity ions with a mass larger than that of the matrix component. This is due to faster expansion of aluminum plasma compared to the copper plasma.
Thus efficiency of acceleration of impurity ions and their recombination increases in aluminum compared to copper due to larger values of ne in aluminum plasma. In doing so, faster expansion of aluminum plasma results in increase of the recombination rate constant with increase of the impurity ion mass.
Influence of a plasma plume lifetime on relative yield of impurity ions
It was shown in [21] that the lifetime of the plasma plume can be changed by changing a laser spot diameter at a target or by changing the mass of the matrix component. The influence of d variation on the relative yield of singly charged impurity ions (or RSC) in a fixed (copper) matrix was discussed in detail in [24,25]. Let us briefly summarize the results of previous studies.
Three intervals of variation of d (or τ0) were distinguished from the point of view of processes in the laser plasma which influence the relative yield of ions. At small values of d (≤0.2mm) or τ0, ionization processes dominate. At d ≤0.2mm the degree of ionization of impurity atoms is determined by their ionization rate constants.
In the second interval of the laser spot diameter variation (≤0.2mm ≤0.6mm), ion acceleration plays an important role and leads to variation of a relative yield of ions because the efficiency of ion acceleration is proportional to the ratio Z/M. In this interval the relative yield of ions of different elements can be equal, however this equality takes place only for several chemical elements. The relative yield of ions of other elements is other than unity and is determined by efficiency of the processes of ionization, ion acceleration and recombination for ions with different values of M and ϕ. The character of this dependence is determined by experimental conditions.
Because in this interval the relative ion yield is controlled by competing processes of acceleration and recombination, calculating this yield for different elements is highly complicated.
At d ≥ 0.6mm the recombination plays the decisive role. In this range of d the absolute value of ionic yield is governed by the nature of the recombination process and by efficiency of ionization and ion acceleration processes (and competition of acceleration and ionization processes).
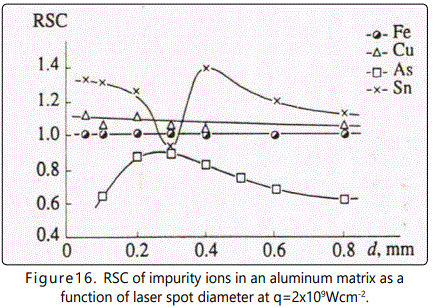
Consider variation of the relative yield of ions at different masses of the matrix component of the plasma plume. Figure 16 shows RSC of impurities in a sample with aluminum matrix as a function of d at q=8 x108Wcm-2. Note that only singly charged ions were taken into account when calculating RSC because their yield amounted to more than 90% of the total number of ions. At d<0.3mm ionization processes dominate. As the laser spot diameter d increases from 0.05 to 0.3mm the value of RSC for Sn drops from 1.30 to 0.91, and the value of RSC for As grows from 0.65 to 0.88. Such behavior of RSC as a function of d for these elements is due to the fact that the first ionization potential of Sn is lower, and that of As is higher, than the first ionization potential of the internal reference element (iron, in the case under consideration). In addition, it is seen that the most striking decrease of RSC for Sn takes place at d ranging from 0.2 to 0.3mm. Variation of RSC with increase of d in this interval is governed by the fact that increase of the plume lifetime results in more effective interaction of electrons with evaporated atoms, which is described by the relation obtained in [24-26]

However, variation of d results in simultaneous variation of τ0 and τi. Thus, at 0.05 ≤ d ≤ 0.3mm the number of ions created is governed by the exponential in Eq. (7).
In the case of admixture of Cu, RSC does not vary as the spot diameter d varies from 0.05mm to 0.3mm. This is explained by equal ionization rate constants (or ionization times) for Cu and Fe atoms.
Let us compare the experimental results with a>priori calculation of RSC using a formula obtained in [24-26]. It was shown that for small d<dmax and moderate values of q, that is, in the case of the dominant yield of singly charged ions in the laser plume, we have:
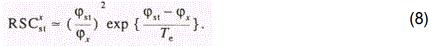
It is seen from Table 3.7 (d=0.05mm, q=1x109Wcm-2) that relation (8) well describes the relative yield of ions in the case of the aluminum matrix, as well. The largest discrepancy ▲ obtained in the case, of As does not exceed 20%. In our calculations we took into account dependence of Te on plasma density and mass of the matrix component, in accordance with Eq. (5). In doing so we assumed that variation of ne as the copper matrix is exchanged for the aluminuft one is determined by variation of the ionization rate constant^ of the matrix atoms, so that as follows from the solution of Eq. (6).
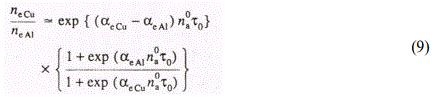
At d>0.3mm the process of ion acceleration is increased. It was shown earlier in [34] that efficiency of acceleration of ions is inversely proportional to their mass. In doing so, accelerated ions gain an excess velocity with respect to the matrix atoms, which can result in effective recharging [10]. Thus recharging of Fe+ ions on A1 atoms is more effective than that of Sn+ ions, due to larger relative velocity gained under acceleration in a double electrical layer. As a result, RSC of Sn increases as d is increased from 0.3mm to 0.4mm. For Cu, RSC does not vary because the difference between the masses of Cu and Fe is small. Thus, in this range of d the relative yield of impurity ions is governed by the competing processes of acceleration and ion recharging. Obviously, the efficiency of both processes depends on the matrix component of the plasma plume. It was shown above that the ionization rate constant of the matrix atoms governs Ne , which in turn influences the efficiency of ion acceleration. In doing so the more effective is the interaction of ions with electrons in the electric double layer, the larger is the relative velocity of ions with respect to that of matrix atoms, leading to increase of the recharging cross-section [10].
At d>0.4mm, ion recombination becomes the dominant process. Contrary to the results obtained for copper, the recombination rate constant is proportional to the mass of an ion (under expansion of the aluminum plasma). Consequently RSC for Sn and As decreases, because MSn and MAs are larger than The essential dependence of αp on M is due to the fact that the matrix mass (Al) is considerably less than the atomic masses of all impurity elements, so that one can speak of partial separation of ions with respect to their masses as the plasma plume in a “nonfrozen” ionization state expands. Weak dependence of αp on M can be explained by friction which results in matrix ions carrying away a fraction of the impurity ions. In doing so the character of the recombination process is governed by the plume parameters and its matrix component [26].
At fixed parameters of target irradiation, efficiency of main processes which occur under multi-component plasma plume formation and expansion is governed by the matrix.
If the laser spot diameter is small, so that processes of ionization dominate in the plasma plume, the absolute yield of impurity ions is determined by the ionization rate constant of the matrix atoms (this constant governs the number of electrons in the plume). In this case the relative yield of impurity ions is determined by the conditions of excitation, and characteristics of the corresponding impurity atoms (their first ionization potentials) and atoms of the matrix (their mass and ionization rate constant), and can be calculated a priori.
The density of electrons ne, which depends on αeM, determines the efficiency of ion acceleration in an electric double layer, provided other conditions are the same. At d>dmax impurity ions effectively recharge on matrix atoms in the plasma plume, the efficiency of recharging increasing for impurity ions with smaller mass.
At d<dmax the recombination of created ions dominates in the plasma plume. The character of recombination depends on the kind of matrix. The recombination rate constant of impurity ions depends on their mass, provided the mass of the matrix ion is largely different from that of the impurity ion, resulting in partial separation of ions with respect to their mass. The efficiency of recombination is also governed by characteristics of the matrix component which determine the time of plasma expansion and the number of “cold” electrons in the plume.
Thus, one can control the absolute yield of impurity ions by changing the matrix component of the plume so that parameters necessary for multi-component laser masss-pectrometry are achieved.
Hydrocarbon background of laser sources
In solving various materials problems in microelectronics, optoelectronics, chemical industry, development of new technologies, etc., there inevitably arises the question of the mass-spectrometric control of the elemental composition of very pure substances, which allows simultaneous detection of all the elements of the periodic table with a detection limit of no worse than 10-6–10-7 at. % and accuracy of 30% without use of any standards.
A very important problem is the detection of gas-forming impurities such as H, N, C, K, and O in pure substances. The presence of background lines of residual gases, such as hydrocarbons, in the laser mass spectra often leads to significant errors during the laser-mass spectroscopic (LMS) analysis in determining the gas-forming impurities and identification of analytical lines in multi-component samples. The LMS analysis of the hydrocarbon background was performed using a JEOL JMS-01-BM-2 double-focusing spark source mass spectrometer. The vacuum in the spark source of ions was 2-10-1 Pa, in an electrostatic analyzer ― 2-10-5 Pa.
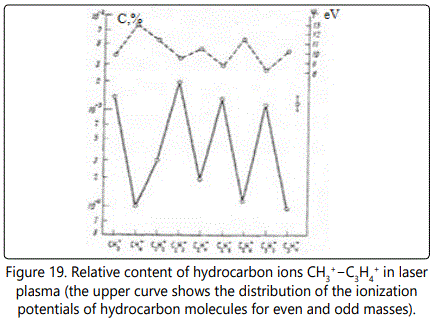
The most intense lines are formed by the ions CH3+, C2H3+, C3H3+, C3H5+, and C3H7+ containing an odd number of hydrogen atoms. The intensity of each of these lines in terms of the concentration may in some cases be as high as 0.8−2×10-3 at.%. Figure 17 shows a fragment of the mass spectrum of an osmium sample with an exposure of the 3 nC. One can see lines of hydrocarbon ions from C2H2+ to C3H+ with their content from 10-4 to 2×10-3 at. %. At an exposure of 20 nC. The mass spectrum of a multicomponent biological object (Figure 18) exhibits lines of hydrocarbon ions from C4H2+ to C5H12+ with their content from 10-6 to 10-4 at. %. In a series of hydrocarbon ions with the number of hydrogen atoms n = 2 to 12, one can observe more intense lines of ions with odd masses in comparison with even masses from 1.5 to 25 times. This phenomenon can be explained by the difference of the ionization potentials of the corresponding molecules and radicals: for odd masses they are lower than the even ones (Figure 19).
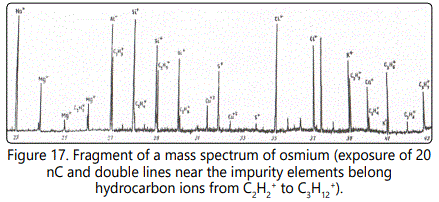
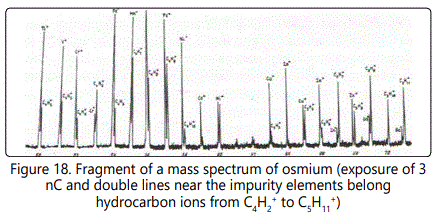
With increasing exposure of 10 to 30 nC in the mass spectra exhibit heavier hydrocarbon ions with n = 7. However, their total number is one or two orders of magnitude lower than that of hydrocarbon ions with n = 2. The total content of hydrocarbons in the mass spectrum amounts to 10-2 at. %. To determine the content of oxygen ions of types CnHmOp+ and to detect them among the hydrocarbon ions require an enhancement of the spectrometer resolution (on the left wing of the analytical lines of heavy hydrocarbons C6Hg+−C7H9+ (in the form of a small step) the corresponding oxygen ions can be present).
When the vacuum in the electrostatic analyzer increases to 5×10-6 Pa and in the ion source of the mass spectrometer to 2×10-5 Pa, the hydrocarbons in the mass spectra at these levels of sensitivity are not detected.
Low-background ion source for a ‘LIDIA’ ultrasensitive mass spectrometer
The search for small amounts of super-heavy atoms in nature requires the use of a highly sensitive and rapid analysis. This can be done by the mass spectroscopy with direct detection of ions. To this end, an ultrasensitive mass spectrometer ‘LIDIA’ was developed, the scheme of which is shown in Figure 20 This mass spectrometer includes a laser-plasma ion source, a vapor or laser target, an electrical system of selection of the ion component, and a multi-split system to reduce the background of rescattered ions. The relative sensitivity of the mass spectrometer is 10-7−10-9 at. %, the sample weight is 100 mg, and the analysis time is 2-3 hours.
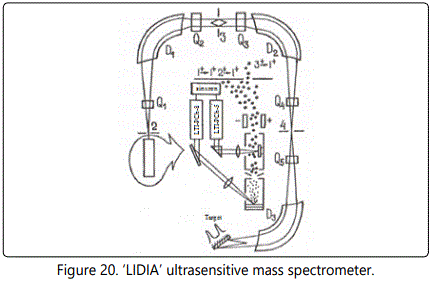
The choice of a laser-plasma ion source is justified by a number of advantages: in the first place, because of the minimal yield of ionized molecular compounds that can result in background mass lines in the region of the atomic mass A = 250. The laser-plasma ion source is also preferable because of the low flow of matter, the possibility of local analysis, the lack of selectivity, and the absence of ionic components not related to the target material.
Laser-plasma source of ions operation characteristics
The laser source was an LTI-PCh-8 solid-state electro-optical Q-switched quantum generator. The energy generated by the laser energy was 60 mJ and the pulse duration was 12 ns. The radiation was focused on the sample surface to a 300-µm-diameter spot. The plasma produced on the target surface expanded inside a 100-mm-long drift tube and reached the module of beam formation and acceleration. The ion beam with an energy of 40 keV was analyzed by a sector magnet in the focal plane of which a Faraday cup was placed. The current pulse signal was observed on an oscilloscope.
In designing the ‘LIDIA’, an additional charge exchange of the ion component is envisaged because the number of molecular ions with increasing ion charge decreases by several orders and the charge exchange process causes an additional decrease in the ionized centers in the flow. Simple evaluations in our experiments show that with the charge exchange 3⁺→1⁺, the relative sensitivity of 10-9 at. % is achieved during 3 hours of the LTI-PCh-8 laser operation at a frequency of 50 Hz. In designing a source for the ‘LIDIA’, operation with singly charged ions is provided against the reduced background of molecular compounds. As was shown, there is a large difference in the energy spectra of atomic and molecular ions, which is effectively used in low-background laser-plasma sources. The simplest way is pre-selection of the ion energy by a decelerating electric field.
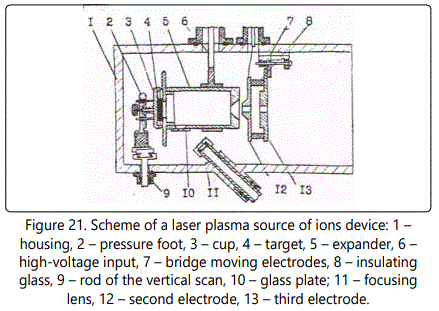
Consider the design of a LPSI (Figure 21). The expander is made in the form of two electrically isolated parts (6) and (9), connected by a fluoroplastic insulator. On the surface of the insulator there is a ridge that prevents the surface of the evaporated material sample from dusting. The rod-holder with an additional electric input connects the various parts of the expander to the low voltage power poles. The ‘plus’ is connected to the end of the expander (6), located near the extracting electrode (12). Inside the expander an electric field is produced and the ion energy can be extracted. The rectified voltage is adjusted through the primary circuit of the transformer. On both sides of the expander a high voltage of up to +40 kV is applied via the ceramic insulator. The sample is mounted on a movable cup (3), and the ions are extracted by the ion optics (12, 13).
After the first series of experiments we found some design defects of this source. In particular, the background of charged molecules is eliminated at a supply voltage of 200 V, which is probably due to the geometry of a locking field (e/d – 1.0) and to the phenomenon of the accelerating voltage drop in the expander volume. To address these disadvantages, we placed additionally in the expander a grid (1×1 mm, 90% transparency), which serves to produce a locking field with the configuration of a plane capacitor. With such a source we studied the yield of charged molecules for specially prepared oxide samples, at a confining potential in the range of 10 – 20 V. The ability to remotely change the confining potential without turning off the high accelerating voltage allows a direct comparison of the oxide yield with and without a confining potential.
At a level of 5×10-6 from the total ion current, we failed to observe charged molecules at 20 V, while at 0 their yield was (1-3)×10-3 for different types of samples. Thus, a LPSI with the energy selection reduces the background level of the molecular ions by 500 times on average, and is one of the main parts of the “LIDIA” facility.
References
- Zeldovich Ya B, Raizer Yu P, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Moscow, Nauka. 1966. doi: 10.1016/B978-0- 12-395672-9.X5001-2



