Abstract

In the current paper we derive the general form of the relativistic Doppler effect and of the relativistic aberration for the case of accelerated motion of the source with respect to an inertial receiver. The formalism enables us to derive the formalism of the IvesStilwell class of experiments for the realistic case of accelerated sources of electromagnetic waves.

Keywords: Accelerated motion, general coordinate transformations, accelerated particles, planar electromagnetic waves, relativistic Doppler effect, relativistic aberration, Ives-Stilwell class of experiments

PACS: 03.30.+p, 52.20.Dq, 52.70.Nc

1. Introduction

In the current paper, we are presenting the equations of electrodynamics in an accelerated frame as a starting point for the derivation of the Doppler effect in the case of uniformly accelerated source. The resultant equations are used for the derivation of the formalism for the Ives-Stilwell class of experiments in the case of uniformly accelerated source.

2. Accelerated Rectilinear Motion – the Transformations of the Electromagnetic Field

Let S represent an inertial system of coordinates and S '(τ) an accelerated one. According to references [1,2] in the accelerated frame S '(τ) the planar wave equation of the electric field E' is :

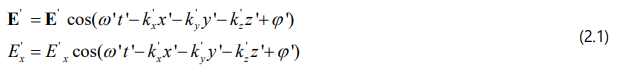
According to references [1-3] the coordinate transformation from the inertial frame S into the accelerated frame S '(τ) is:

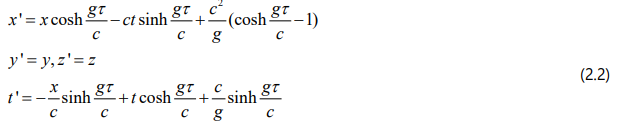
where “c” is the speed of light in vacuum, “g” is the proper acceleration, τ is the proper time. Substituting (2.2) into (2.1) we obtain:

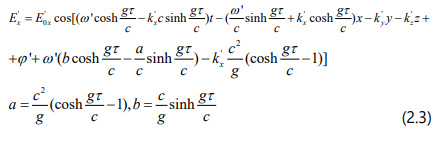
On the other hand, in the inertial frame S, the wave equation is:

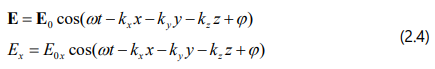
Since references [1,2] demonstrated that E'_x = E_x it follows that:

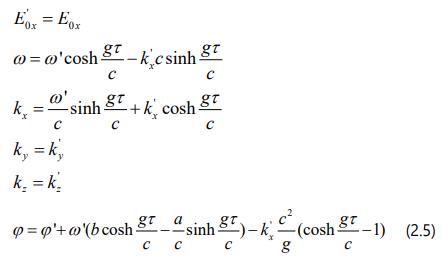
The formula 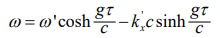represents the general formula of the Doppler effect due to acceleration.

3. The Theory of the Ives-Stilwell Class of Experiments for the Case of Uniformly Accelerated Source

One of the glossed over issues with the Ives-Stilwell experiment is the fact that the ions that act as light sources are, in fact, in accelerated motion under the electric field. For example, the 1938 experiment [4] used a 20,000V potential difference. In the 1941 experiment [5] a four-electrode version of the canal ray tube with three gaps was used, producing a total potential difference of 43,000 volts. A voltage drop of 5,000 volts was used across the first gap, while the remaining voltage drop was distributed between the second and third gaps. In fact, all the experiments in the Ives-Stilwell class [6- 16] rely on accelerated, not uniform motion of the source. Hence, the correct formalism needs to rely on the accelerated Doppler effect (2.5). Considering two counter-propagating waves, we can derive the average pulsation:

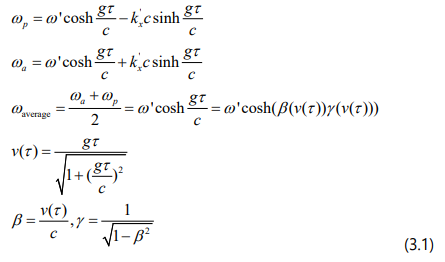
In (3.1) , ω_p ω_a represent the pulsations of the light waves emitted by the ions moving alongside an arbitrary line, in opposite directions (parallel and anti-parallel, respectively). Notice the similarity to the formalism ω_average = ω'γ (v) derived for uniform motion of the ions [6,15,16].

Notice that:

At the speeds at which the Ives-Stilwell experiments are being conducted [7-14], β = 0.064 so expressions (3.2) and (3.3) are very close. At higher speeds, though, the expressions start diverging from each other so the exact formalism derived in this paper becomes necessary.

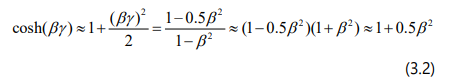
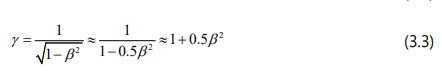
Conclusions

We constructed the general formalism for the case of the accelerated Doppler effect between the frame S '(τ) co-moving with an accelerated particle in rectilinear motion into an inertial frame of reference S. The solution is of great interest for real life applications, because it enabled us to derive the formalism for the Ives-Stilwell experiment in the case of accelerated source.

References

1. Sfarti A. Electrodynamics in Accelerated Frames. Th Phys. 2017; 2(4). doi: 10.22606/tp.2017.24003   
2. Sfarti A. Electrodynamics in Uniformly Accelerated Frames as Viewed from an Inertial Frame. IJPOT. 2017; 3(1).   
3. Sfarti A. Generalization of Coordinate Transformations between Accelerated and Inertial Frames – General Formulas of Thomas recession. JAPSI. 2017; 8(2).   
4. Ives HE, Stilwell GR. An experimental study of the rate of a moving atomic clock. J Opt Soc Am. 1938; 28(7).   
5. Ives HE, Stilwell GR. An experimental study of the rate of a moving atomic clock II. J Opt Soc Am. 1941; 31(5).   
6. Sfarti A. Detection of Light Speed Anisotropy via a High Speed IvesStilwell Experiment. CJP. 2008; 86(5). doi: 10.1139/p07-120   
7. H Müller, C Braxmaier, S Herrmann, O Pradl, C Lämmerzahl, J Mlynek, et al. Testing the foundations of relativity using cryogenic optical resonators. Int J Mod Phys D. 2002; 11: 1101-1108. doi: 10.1142/S0218271802002608   
8. H Müller, C Braxmaier, S Herrmann, A Peters, C Lämmerzahl. Electromagnetic cavities and Lorentz invariance violation. Phys Rev D. 2003; 67: 056006. doi: 10.1103/PhysRevD.67.056006   
9. A Brillet, JL Hall. Improved Laser Test of the Isotropy of Space. Phys Rev Lett. 1979; 42(549). doi: 10.1103/PhysRevLett.42.549   
10. JA Lipa, JA Nissen, S Wang, DA Stricker, D Avaloff. New Limit on Signals of Lorentz Violation in Electrodynamics. Phys Rev Lett. 2003; 90060403. doi: 10.1103/PhysRevLett.90.060403   
11. C Braxmaier, H Müller, O Pradl, J Mlynek, A Peters, S Schiller. Test of Relativity using a cryogenic optical resonator. Phys Rev Lett. 2002; 88: 010401. doi: 10.1103/PhysRevLett.88.010401   
12. P Wolf, S Bize, A Clairon, A Luiten, G Santarelli, M Tobar. Test of relativity using a microwave resonator. Phys Rev Lett. 2003; 90 060402. doi: 10.1103/PhysRevLett.90.060402   
13. M Kretzschmar. Doppler spectroscopy on relativistic particle beams in the light of a test theory of special relativity. Zeitschrift fur Physik. 1992; A 342(4): 463-469.   
14. G Saathoff. Improved Test of Time Dilation in Special Relativity. Phys Rev Lett. 2003; 91: 190403. doi: 10.1103/PhysRevLett.91.190403   
15. Sfarti A. Special relativity optical cavity experiments explained from he perspective of the rotating frame. MPLA. 2022; 37(3). doi: 10.1142/S0217732322500146   
16. Sfarti A. Special relativity experiments explained from the perspective of the rotating frame. MPLA. 2019; 34(21). doi: 10.1142/S0217732319502559