Abstract

In this paper, we try to discover the shape of the universe based on the influence that it has on some of the laws of physics. Specifically, we examine the famous equations of the special relativity and conclude that those equations can be only valid and described well, if we are living on a closed universe. This is a novel approach that we took for determining the shape of the universe.

Keywords: Universe, Shape of the Universe, Four-dimensional space, Cosmology.

Introduction

Are we living in a finite universe? If we are, how much is its size and mass? How can we imagine boundaries for our universe? These questions have been the matter of debate in the past century and their answers lie in the field of cosmology. It is well known that the universe can be described based on one of the following models.

• Flat or Euclidean Universe spread infinitely, and it does not have any boundaries.

• Open Universe which has a negative curvature, spreading infinitely without any boundaries

• Closed Universe, which has a positive curvature like a sphere. Therefore, both its size and mass are finite, but like a sphere it does not have any center or edges.

To find out which model is correct, we can use the Friedmann equations. According to this equation if the average density of the universe is higher than a critical value, then we can say that we are living on a closed universe. On the other hand, if the average density of the universe is below the critical density required by the Friedmann equation, the universe is open. In other words, the density of the universe plays a critical role in our judgement about the shape of the universe and unfortunately we cannot precisely determine the average density due to some reasons such as the amount of black matter in the universe.

There is a fundamental law in the cosmology stating that the same laws of physics existing on our planet also governs across the universe for all time. Therefore, as we can say the structure of the universe follows the same laws of the physics governing the nature, the laws of the physics are influenced by the structure of the universe as well. In other words, there is a bilateral relation between the laws of the physics and the shape of the universe[1].

Based on the aforementioned principal, although there are some physical laws which can be valid regardless of the shape of the universe, the validity of some laws strongly relies on the model of the universe. This principal gives us a novel different approach that we can use for understanding the shape of the universe. In the rest of the paper, we assume that we are living on a closed universe curving back on itself like a sphere but in a four-dimensional space. Then, based on that assumption we obtain some equations explaining the behaviour of an object in our universe. If its behaviour matches our experiences and the other well-known laws of physics, it means that our assumption has been correct.

The Dimensions of the Universe

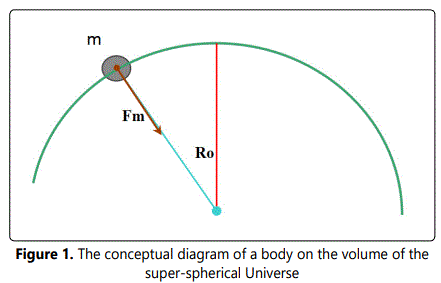
Assuming that the universe is finite and there is a body with the mass of m inside it (Fig.1). The net gravitational force exerted on the body by the rest masses is expressed by:

Where,

G = gravitational Constant

R_O = the effective radius of the universe

M_O = the effective mass of the universe

If that body moves with the velocity of V, a centrifugal force will be sensed by the body due to the curvature of the universe (Fig.2). It equals to:

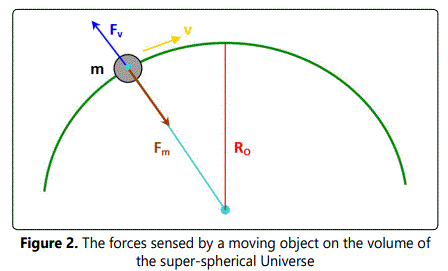
If F_m is balanced by F_v, V will be the most theoretical speed that a body can take. Because if F_v becomes greater than , the body will get out of the space of the universe.

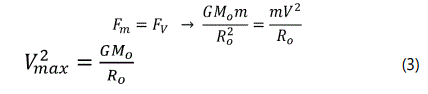
Moreover, it is experimentally confirmed that no object, in the universe, can exceed the speed of light in the free space. Hence, it is reasonable to substitute the speed of light for the maximum speed given by “Eq. (3)”.

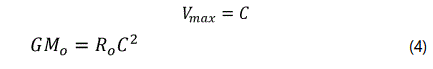
The constituents of the “Eq (4)” are fundamentals of the universe. Therefore, we name it the equation of the universe. The equation of the universe will lead to some consequences. If we can confirm those consequences, then we can say that the equation of the universe is correct. This confirmation will in turn result in being on a closed universe.

The Mass and Energy Relation

Assuming the universe is finite, the gravitational binding energy of a body with the mass of m to the universe equals to:

According to the equation of the universe (“Eq 4”):

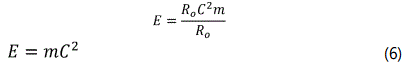
We are all familiar with “Eq (6)”. But it conveys a concept that is quite different from the equation stated in the theory of relativity[2]. The proof of this equation in a way that is related to the mass and the radius of the universe have been firstly presented in this paper.

If the universe was not finite, such a simple and reasonable equation that coincides with the most famous equation of Einstein would not be yielded. So, if the “Eq (6)” is correct, the equation of the universe is undoubtedly confirmed and the universe that we are living on is finite. In the rest, other reasons will be mentioned.

The Cosmic Weight

The “Eq (1)” gives us the gravitational force sensed by a stationary body with the mass of m in the universe. We name this force, cosmic weight and denote it with D_o.

If we plug the “Eq (4)” into the “Eq (7)”, then:

The cosmic weight of this body moving with the velocity of V is represented by D_v:

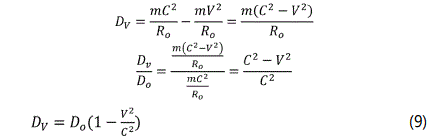
It can be inferred from the “Eq (9)” that the factor (1-v²/c²) in the theory of relativity results from the finiteness of the universe. In other words, the equations asserted by the theory of relativity can be correct only in a finite universe.

Conclusion

In conclusion, some of the laws in physics can be well described if we are living on a closed super-spherical universe. Moreover, the method that we used in this paper also provides us with more profound comprehension of some of the wellknown Einsteinʼs equations. This, in turn, brings about several new relations and explanations which can be the subject of the future works and publications.

References

1. A. E. Meybodi. Hasti Physics, 1st Edition. 2013; ISBN : 964-06-2117-X   
2. A. Einstein. The meaning of relativity, Princeton University Press.