Abstract

The consistency of cosmological models is discussed with its implications for negative Ricci curvature and new global topological constraints. Quantified consequences seem to fit observations and may contribute to solve recent cosmological issues such as flatness and the effect commonly interpreted as dark energy or cosmological constant, by applying to metrics a Statistical Physics random K-SATisfiability formulation of consistency

Keywords: Cosmological parameters, Dark energy, Early universe, Large-scale structure of universe, Cosmology: observations

1. Introduction

A brief summary and state of the art about current issues in cosmology, in the second part of this introduction, follows a preamble, hereafter, on some classical assumptions underlying the current ‘consensusʼ FLRW model, about which Ellis and van Elst [7] write that it cannot fit with the behavior of our universe – locally inhomogeneous – and prefer to speak of “quasi-FLRW”.

Preamble

Apart the multi-universe hypothesis ‘ourʼ universe is classically assumed globally hyperbolic, time oriented along Cauchy hypersurfaces and diffeomorphic to R x M³ where the three-dimensional section M³ is endowed with a given topology. This condition is “difficult to justify on physical grounds” writes Lachièze-Rey and Luminet [18], “except if one believes in strong determinism” i.e. here that “the entire spacetime can be calculated from the information on a single hypersurface”.

Releasing such a basis relieves this condition, especially if other, less tightening global constraints might compete. In fact one may want to look for the least restrictive constraint among all possible Constraint Satisfaction problems. There are in fact observations, such as entanglement, and assumptions for instance in the HartleHawking model mentioned below, that militate for envisioning some limits to the extent of this specific strong determinism, as well as limits to the gravitational phenomenon as compared to others, such as electromagnetism.

A global constraint of logical Consistency is an example, considered in the present paper even though the second principle of thermodynamics suggests another one, thereby questioning their interdependence or common consistency, which may have to be found in statistics. More precisely the first one, through the Constraint SATisfiability model here proposed, may set spatial bounds while the ‘second lawʼ drives a global time-orientation then less restricted by a single topology.

In fact constraints from the second law, implying paths along a rigorous series of boxes of increasing phase space volume are therefore envisaged by Penrose [12], even possibly ultimately infinite and furthermore PU “infinite dimensional whether or not the universe U is finite in extent”. Meanwhile another paper [43] went to present “A new topology” meant to incorporate “the causal, differential and conformal structures” after preliminary observations including a conclusion from Zeeman about causality implying a partial ordering – preserving the Lorentz metric – and a theorem of Hawking relating “causal to differential structure”. Relationships between causality and consistency on the one hand and between entropy and differential structure on the other hand, must be accounted for and the conclusion of the present paper comes back to these issues.

The Hartle-Hawking scheme [11] came a few years later with a proposal for a “Ground-state wave function” and where (part III) they consider cases with a cosmological constant Λ > 0 but “regard Λ = 0” as a limiting case. Putting aside the Planck length l = (16πG)^½ – normalized to one in the remainder of this paper – the action for their quantum gravitational path integral model writes:

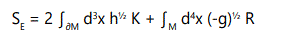
K is here the trace of the extrinsic curvature of the three-surface bounding four-dimensional M⁴ . They later shift a Lorentzian K_L transformed into Euclidean K by Wick rotation t→ iτ and metrics of Euclidean space of greatest symmetry, for the case Λ = 0, such as:

Their set of underlying assumptions about using the Wheeler-de Witt equation and the Wick rotation has been much debated and our purpose here is solely to exhibit a well-known case introducing flexibility in the topology of the gravitational field under original global constraint (here a quantum gravity path integral evolving under this global equation). Penrose pinpoints that one advantage and reason of choice of this Euclidean 4-space as opposed to Minkowskian is that its rotation group O(4) has finite volume as opposed to Lorentzian infinite volume of O(3,1). Hartle-Hawking comment their scheme for the “Euclidean four-sphere of radius 1/H” – growing with the Hubble parameter constantly decreasing – that their bounding three-spheres are either with positive or negative K and that “the action tends to its flat-space value (zero) as K tends to positive infinity” (and to) “the Euclidean action for all of de Sitter space as K tends to negative infinity”. Now the model of the present paper rather focuses on how local and initial splits of quanta of positive versus negative curvature may happen and entail. Therefore this HartleHawking model [11] is a valuable reference for the proposal of the present paper, yet relies on its own set of global constraints, which frame the options for these hʼ_ij and h”_ij three-geometries there assumed defined on respectively initial and final spacelike surfaces, which precisely are at stake. They start with a global assumption of spatially homogeneous, isotropic, closed universes with S³ topology but their section VIII loosens this set by allowing “all possible three-topologies” and for instance envisioning “N compact disconnected threegeometries”. Their global geometry is still a space-time foursphere with its symmetrical bounding N three-geometries “cut out of it” and it does not matter where the cutting takes place provided “they do not overlap”. In fact N is also presented as the size of a configuration space and yet one configuration should start with a lowest entropy, indeed spatial extent (their “single point” or ‘nothingʼ) – and why not dimensionality – and have N grow as a finite set of such elementary disconnected points or space quanta, as proposed in the present paper but with a configuration space much faster growing in relation to the power set of the spatial configurations inasmuch as local symmetries may be formally integrated into a global true or ‘satisfiedʼ model.

These features are emphasized in this introduction and even preamble where some references are given for the proposal of the present paper even though underlying constraints somehow differ, being on a global logical consistency requirement in a discrete context rather than grounded on a wave-function functional integral driving process. Observe already, however, than pushing to the limit the option opened by Hartle-Hawking of ‘cutting outʼ the N three-geometries anywhere should allow the consideration of the largest set of minimal, in fact quantum-size such threegeometries, especially considering the integration of the second law as a global constraint, cf. below.

Dimensionality and differentiability of the universe

Barrow & Tipler [15] pinpoint that, for Euclidean space R^N, it is only for N = 4 that the number of differentiable structures is uncountable. More precisely, producing a different proof of Donaldsonʼs results, Freedman & Uhlenbeck [44] pinpoint for dimension 4 a result of Quinnʼs that “all compact 4-manifolds are almost smooth, that is smoothable in the complement of any point” while “in lower dimensions any topological manifold admits a unique smooth structure (up to diffeomorphism) and in higher dimensions smooth structures correspond to reductions of the tangent bundle”. They wonder, as well as Penrose, but as well as Computational complexity references hereunder such as Cookʼs, at the specific powers therefore endowed to three-dimensional to four-dimensional spaces.

Recall now, from above, Hawkingʼs theorem linking causal to differentiable structure and the remarks from Penrose: in a growth of structure of the universe carrying both an increase of dimensionality and topological and geometrical aspects, the diversity of non-four-dimensional structures appear meager among the set of four-dimensional differentiated structures and as well then for Euclidean versus Lorentzian metrics in a four-dimensional universe, for which the diversity of structures donʼt even compel a priori global homogeneity or even a priori given topology.

The uncountable set of structures, hence of phase space infinite volume, hence of potential entropy, itself opens the question of the consistency and completeness of such a set, that a universe should tend to satisfy through an expansion that appears on the one hand to extend itʼs a priori void, sheer or gravitational space and the other hand to diversify and complexify its content toward ever more integrated and complex and yet still four-dimensional substructures. This is where Complexity theory or computational and formal linguistics scientific fields, with Category theory, are involved.

About languages and models of the universe

Hopcroft & Ullmann [46] highlight that the set of languages – itself a subset of human, Natural language – is non-countably infinite (hence dense or smooth), being the power set of the set of sentences or words (playing as atomic predicates or propositions). This applies to mathematical language and to any model in mathematical physics, whether in Quantum Mechanics, General Relativity, Cosmology but only inasmuch as a first infinity N → ∞ were effectively accessible. Everything otherwise remains just finite and not even a single integration could be achieved. This pertains to the customary position of the observer assumed asymptotically posted “at infinity” to the opposite of singularities such as the Big Bang, or Black Holes, or in fact those diverse “Terminal Indecomposable” past or future singularities proposed by Penrose, adding to these most known two eventual White Holes (of same category than the Big Bang) and Big Crunch (same as Black Holes). These observers are critical in Relativity as well as Quantum Mechanics and terms such as ‘IGUSʼ, coined by Dower & Kent and thereafter applied by Gell-Mann & Hartle as ‘Information Gatherers and Utilizersʼ, have their seemingly equivalent in Computational complexity as ‘oraclesʼ, as defined by Turing himself and pervading many verified theorems of the field of Computational complexity.

An example is given below, from foundational Cookʼs [8] paper about the complexity class SAT, particularly for its specific two-dimensional 2-SAT, belonging to the class P (Polynomial Time complexity) as opposed to threedimensional 3-SAT, shown NP-Complete, where NP stands for Non-deterministic Polynomial, radically more powerful and complex. This is introduced here because an equivalent jump of complexity is hereafter envisioned to occur from 2-dimensional to 3-dimensional space and then fourdimensional space-time with time dimensionality added, but where space unfolds in a finite discrete quantized manner under the primary constraint of SATisfiability.

A model with expanding SATisfiability, such as presented in this paper, may contribute to bridge effectively a local finite, discrete past to the global term(s) where the universe effectively summarizes as a consistent object. Penrose concludes his book [12] by envisioning a cosmological model without a priori given spacetime manifold and rather based on discrete and probabilistic elements, from which followed his endeavor to a spin networks picture (e.g. pages 946 - 966, [12]). Hartle-Hawkingʼs picture briefly commented above with its “N compact disconnected three-geometries” generalization, appears to involve such number of objects with N growing (being a normalization factor but occasionally with the role of the scale factor or otherwise of configuration space size). The path integral may be assumed to select the dominant contribution(s) to the growth of entropy. An increasing number of interchangeable such contributions as spatial cells of definite curvature within a still finite configuration space seems fit to maximize it.

In fact the model presented in the present paper appears to comply with this recommendation, maintaining the ground-state of a flat universe split between two types of regions as N grows, i.e. in negatively curved cosmic voids versus positively curved halos, keeping average null curvature, yet with the negative curvature spatially spreading while the positive curvature regions collapse.

Furthermore, Hartle-Hawking picture is known to apply to the gravitational field itself the Feynman path integral approach of Quantum Field Theories, hence toward a Quantum Gravity project, thereby extending Bohrʼs conclusion of completeness of Quantum Mechanics to Cosmology. But that should keep such completeness of the QM sort of logical formalism, or non-local consistency, throughout a field that appears precisely to carry what local reality means. Penrose devoted several pages to this observation that the configuration space becomes, at least locally, maximal through attraction by culminating in Black Holes, as opposed to the global maximum entropy reached through comprehensive homogeneity of dynamics for a gas.

As a provisional remark or conclusion of these preamble remainders, a non-local consistency should be explained, whereby a global dissymmetry unfolds, and may even be computed and tested, from otherwise a priori homogeneous and maximally symmetric a gravitational field universe, within which a symmetry of content, radiation and then matter, arises. This is a task to which the present paper brings a novel, as far as we know, viewpoint by applying successful results from Statistical Physics and Constraint Satisfaction Problems solving.

It appears that these random k-SAT techniques exhibit phase transitions with measurable thresholds from which are achieved splitting only solvable with the emergence of more complex objects of which terminal cases are the Black Holes, with a maximally dissymmetric contribution to entropy versus the cosmic voids. For that purpose, to the creation of quantum particle pairs especially in the very first moments of the universe will here be assumed a previous – possibly inflationary – creation of quantum spatial bits or sections pairs, or at least interpretable as such.

Inflation as an explanation of the flatness of the universe

Penrose [12] as well as Lachièze-Rey and Luminet [18] both express doubts about inflation, if any or alone, to be able to result in the highly homogeneous, flat space such as exhibited by the CMB. For instance [18] write that “convincing arguments in favor of inflation only exist in models where space was already homogeneous before inflation”.

The SAT-based model presented in this paper brings a process naturally ensuring flatness through its metrics creation preserving the ground-state central to other SAT applications in physics quoted below [10] as well as to the Hartle-Hawking model. This discrete, effective process, does not however contradict inflation, as briefly commented in the discussion and conclusion, if only considering the de Sitter type of expansion entailed. A more detailed analysis might dedicate to the ‘homogeneityʼ aspect.

Current issues about the measurement of cosmological parameters

Our universe appears improbably to have all along remained nearly flat, with what is interpreted as a repulsive dark energy component or a cosmological constant Λ which is hypothesized, according to the ΛCDM dominant model, in effect lately to fill the growing difference between the energy density ratio of matter (dark + baryonic) Ω_M and 1, thereby allowing the gravitational field own ratio Ω_k to remain nearly null, within a circa 10-3 margin. This model relies on precisely tested Einsteinʼs local theory of General Relativity [1, 2, 3], complemented by assumptions of a universe a priori homogeneous and isotropic, restricting the choice of possible topologies.

Since measurements of the Hubble parameter keep diverging between circa 67 and 73.5 km/s/Mpc [4, 5, 6], the limits of this consensus model become debated. Particularly at stake is this ‘lateʼ (in cosmological time) increasing repulsive effect quantified as ΩΛ and possibly even a ‘late lateʼ “sharper acceleration” [23]. The solution of the impact of a local large void surrounding the Milky-Way and resulting in our observational perspective being biased, has been modeled by [21] and tested using a Lemaître-Tolman-Bondi isotropic but inhomogeneous model for such a void. This has led these authors conclude that such a local fluctuation may not account for the divergence.

About the consistency of the universe

The consistency of the universe is a ‘key issueʼ ([7], 2.5), and [15] even conclude on a logically closing, complete universe. Would however such a completeness be compatible with Gödelʼs incompleteness theorem? Such a question might apply to a Wave-function model of the universe as well, unless some phenomena, presumably out of the gravitational reach, may unfold out of it, but then how? A mechanism for this subsequent issue is proposed in the second part of the present paper. A comment of Girardʼs [45] is worth a mention here, about how to interpret this specific theorem of Gödelʼs and emphasizing its unpredictability: “a definition, whatsoever, of the next axiom, contradicts the incompleteness”. A complement of formulation (next axiom or clauses) should have to occur, consistently with the second law, by bearing the opportunity for a wider range of options or degrees of freedom although that could encompass bringing in spatial extension and new metric quanta, as considered in the first part of the ‘consistentʼ cosmological model section of the present paper, or new fields, as envisaged in the extended formulation in the same section. This supports the randomness perspective, indeed implicit in any Feynman path based model, hence in the Hartle-Hawking, but here genuinely accounted for in the random k-SAT adapted processes.

Barrow & Tipler [15] interpret their model as that “the universe, which is defined as everything that actually exists, is equal to all logically consistent possibilities¹ ” This emphasizes the major issue of the logical consistent completeness of such models or even of generally modeling the evolution of the universe toward some predefined end or boundary apart... a mere consistency requirement. In that sense, a recursively enumerated process (type 0 language), such as proposed herein, should do better than a less powerful, always terminating type 1 (algorithm), questioning theories such as Misnerʼs [15], whereby an homogeneous and isotropic structure derives from chaos, or such as a Weyl curvature filled ending universe ‘à la Penroseʼ, or even the now observed ‘all scale structureʼ joyfully mixing extremes ranging from cosmic black holes to cosmic voids, hence as discussed in the sections 4 (observational references) and 5 (discussion) of the present paper.

The recourse, in Cosmology, to models using components from logic, formal linguistics and computational complexity, may appear odd, or even illegitimate. Fortnow [40] recalls another seminal work of Cookʼs (1988), to which he adds that it was afterwards proven by Robson to apply to random-access Turing machines, hence relevant for the random-SAT models, which have meanwhile proven efficient to predict the behavior of diverse phenomena in condensed-matter physics. The lemma, which is also highlighted by Mézard [10], writes: “Let M be a non-deterministic Turing machine² running in time t(n), there is a O(t(n)log(t(n)) time and O(log(t(n)) space algorithm that maps inputs x of length n to formulae φ of size O(t(n)) log(t(n)) such that:

x ∈ L ⇔ φ ∈ SAT”

These sorts of relationships may again seem irrelevant or foreign to cosmological issues but the diffusion of discrete phenomena through random walks and paths along graphs with diverse velocities has become useful for a growing series of physical problems and the model herein proposed is related to such type of expansion of space rather than velocity through spacetime. And models of spatial or spacetime expansion will themselves process related algorithms. Morvan & Stirling [50] for instance refer to research on infinite structures and equivalence between infinite state systems and infinite transition graphs to “prove that the traces of rational graphs coincide exactly with the context-sensitive languages”. These csl are the type 1 languages and the traces of rational graphs are the sets of all paths traces (sequences of labels) that start at some initial vertex and end at some final one. Monasson & Zecchina [51] present an energy function associated to the K-SAT problems, whereby “the logical values of the xʼs are represented by N binary variables Si ʼs called spins” through a mapping S_i = -1 (if x_i false) versus +1 (if x_i true). In the present paper the mapping will rather related a quantum of negative curvature to true and positive to false for reasons explained although there is some arbitrariness since logical false versus true transfer to some kind of inversion in physics (which would be spins, matter versus antimatter, etc.).

Mézard [10] generalizes this approach to multiple Constraint Satisfaction Problems in Physics and shows a clustering arising through well defined and observed phase transitions from their energy function, shown equal to one for each violated clause so that the rise of UNSATisfied clusters with the number of clauses, M, corresponds to an increasing ratio of above-ground-state, i.e. E > 0.

The application to underlying space itself, in the present paper, rather keeps overall energy null, hence the gravitational field in average Euclidean ground-state, while clusters of respectively negative and positive energy split in regions interpreted as respectively repulsive and attractive. To the anticipate here a possible corollary to the Uni-SAT model as formula herein presented, recall that the choice of using an Euclidean action is presented by Hartle-Hawking as ‘naturalʼ because better defined for path integrals than the Lorentzian, while this proposed model of SATisfiable metrics results in distinguishing Lorentzian geometries, widened to all mixed signatures, as those SATisfiying precisely as less definable, i.e. un-terminated as opposed to determinate.

As a summary, the present paper drafts a Statistical Physics model according to which this global consistency requirement would trigger an ongoing natural ‘flat-spaceʼ expansion, from within the first 10^-43s to the late era locally inhomogeneous universe observed and which may, as a test, account for the divergence of measurements of the Hubble parameter from a global rather than local causality. It applies a reducibility of general Constraint Satisfaction Problems (CSPs) to Boolean random SATisfiability formulae, already successful in Statistical or Condensed Matter Physics.

Ordering of the sections of this paper

Complexity theory random k-SAT mechanisms are presented in section 2, the presently proposed application to Cosmology in section 3 and diverse referenced observational results from fields in Astrophysics (Cosmic voids) and Cosmology (measurements of the Hubble parameter), as well as in Computational Complexity in section 4.

Some issues are discussed in section 5 and a conclusion fills the section 6.

2. k-SAT Models

Cook [8] proved two theorems about Non-deterministic Polynomial complexity level Logical (consistency) problems reducibility to DNF and even 3-DNF SATisfiability formulae (3-SAT using DNF) or equivalently to 3-CNF since Disjunctive Normal Forms are convertible into Conjunctive. More precisely Cook uses the Davis-Putnam procedure “to determine whether a given formula in Conjunctive Normal Form is SATisfiable” as an efficient way to solve DNF cumbersome problems by recalling that the ‘dualʼ procedure is to determine “whether a formula in disjunctive normal form is a tautology”. Relationships with Geometry, cf. e.g. [9], and Statistical Physics, were also shown.

Applicability of random k-SAT processes in Physics

Random k-SAT formulae target phenomena that are describable from a growing number of N random Boolean variables assigned to a system of M clauses, each clause being made of exactly k variables linked by ORs, but clauses linked through ANDs (conversely for DNF) in the formula.

The random variables represented by x_i and as negated by x_i, compensate on average (for instance with as many spins +1 than -1) when assigned to the formula of M ‘Constraintsʼ. This will well fit, when applied in Physics, spontaneous pair creations keeping a zero or ground state energy budget.

A typical 3-CNF example writes:

Φ = (x₄ ∨ x₅₇ ∨ x₁₃) ∧ (x₉ ∨ x₅₇ ∨ x₂₆) ∧ etc.

while the general case writes:

Φ = ∧_i=1^M (∨_j=1^k a_ij)

where the a_ij are filled with some random set of N balanced x_n and x_n as mentioned above.

One idea behind applying k-SAT is that, while the Constraint Equations from the Field are local the underlying consistency requirement must be global, as for instance assumed by the very idea of a cosmological model, or of a wave function of the universe or even of a universe, whether part of a larger multiverse (still hypothetically consistent) or not. Conversely randomness, with its probabilistic and entropic consequences, is required and carried through the Feynman path integral computations, whatever the quantum field upon which they are applied.

Meanwhile, Complexity theory [13] applied in computational measurements has observed ‘phase transitionsʼ at thresholds, depending on k, of the ‘clause densityʼ ratio α = M/N, for which consequences³ for diverse problems in Physics have been modeled [10, 16, 17, 19, 20]. These thresholds, for which numerical values are commented in section 4, correspond to transitions from easily SATisfied contexts (EASY-SAT) when the number of clauses M is relatively low as compared to the number of variables N, then becomes difficult (HARD-SAT) and finally almost impossible (UNSAT).

Furthermore, Fortnow 14] introduced “relativized 3-CNF” formulae with clauses such as:

‘ʼC_i ≡ x_i1 ∨ x_i2 ∨ x_i3 ∨ A(x_j1,.... , x_jn)ʼʼ

where A(x_j1,.... , x_jn) are Turingʼs ‘oraclesʼ, here interpreted as physically embedding local environment or the boundaries of what defines the clauses of the system considered, which may be the curvature of spatial cells in the case of the domain D of a gravitational system. This addition may also be interpreted as an opening to a fourth dimension, computationally a transition toward 4-SAT and beyond (which have their own measured α thresholds), but physically to a transition from a local to global timelike dimension. For instance in the present application a time as common term of a Cauchy hypersurface to which it brings consistency as it bears some capacity to SATisfy the subset of Boolean clauses of a given random formula that are not SATisfied (UNSAT) by a given assignment of N variables. This addition of a fourth dimension as time is explicated in the next section.

The application to cosmology below therefore will sever both, complementary subsets, known as SAT and UNSAT in the logical, Complexity theory world but now considered for an application to the gravitational field starting from local General Relativity.

Computations of entropy, depending on the field on which the Constraint SATisfiability process is applied, are discussed in the referenced literature. For the present application to Cosmology it is commented in the section 5.

3. Application to Cosmology

A basic formulation of the Einstein-Hilbert action, from which the field equations of General Relativity can be derived, is here considered with neither a priori matter nor electromagnetic, dark matter or dark energy fields, hence with only a genuine gravitational field (as not accounted in the energy-momentum tensor), but here separating positive and negative curvature R volumes:

S_R = 1/(16πG) (∫d⁴ x R⁺ √-det(g) + ∫d⁴ x R^- √-det(g)) (1)

where R⁺ and R^- are respectively positively and negatively Ricci curved and the integration is primarily over a common domain D. This assumes that both sets may be separately integrated (such assumption being previously mentioned about the Hartle-Hawking model), but is compatible with an Einstein-Hilbert action for a sheer gravitational field of basically null, ground-state energy and with a then progressive local General Relativity induced severing into micro and afterwards macro-domains each of constant sign and possibly even constant curvature as pinpointed below, and topologies thence more consequential than causal. Lagrangians for a boundary and for matter and even radiation are here left aside as assumed emerging as a consequence of the model. The det(g) are normalized to one since the process here described precedes and underlies the diversification of metrics that will come afterwards and above, if only from matter hereunder assumed born from the UNSAT part of the formulation summarized in the present section (radiation is another issue). The action can then be split even further to the quantum level, where the timelike variable is integrated separately and where the integral of spatial cells falls into a discrete, quantized series. [18] pinpoint that “almost all 3-manifolds can be endowed with a hyperbolic structure” while [12] emphasizes that quantum experiments work like Yes/No answers to quantum measurement questions, conveying to the extension, here assumed, of such a behavior for quantum gravity even though the equations, in all cases, manipulate the continuum. Meanwhile scalar curvature classically derives as the trace of the Ricci curvature tensor and itself from assumed given metric(s), supposedly smooth.

However, the full splitting derived above from the Einstein-Hilbert action entails a picture of metric quanta emerging from non-localized common vacuum as pairs with associated bits of negative or positive curvature. This basic Einstein-Hilbert action for a provisionally isolated gravitational field therefore writes, ignoring the 1/16πG factor and with |det(g)| = 1:

S_R ∝ ∑₊ δ(xⁱ ) R⁺ + ∑_- δ(x^j ) R^- (2)

where the direction of the elementary δ(xⁱ ) is a spatial direction of measurement along which is tested the question of whether its associated bit of curvature would be positive (here taken as No) or negative (Yes)⁴ . Recall Einsteinʼs thought experiment – and presumably actual experiments since then – of gravitation measured along some axis of acceleration. A precedent might be found in the system of all possible elementary triangulations by [35] with the x_n to be seen as unit causal triangles (these having in their model two spacelike unit edges (a² = - 1) and one time-like with squared edge length a² = 1). In the present model however the three directions are spatial and each may separately be considered to be measured as direction of action. Hereunder basis vectors ei replace xⁱ , if only to avoid the confusion with the a priori distinct Boolean xⁱ variables previously mentioned. Only the spatial vectors are considered, time being associated to the oracles becoming necessary for the UNSAT subset of a priori non-relativized clauses and only then SATisfied.

The scheme proposed below, using random k-SAT metric quanta of elementary curvature as variables, implies how boundary would derive for the positive curvature bits progressively clustering in their compact closed specific regions as opposed to the open regions clustering the negative curvature elements, spatially isolated and yet within a common globally SATisfiable open hyperbolic regime thereby driving the spatial expansion of the universe from its jammed set of cosmic voids. Spin networks, Loop quantum variables, Regge calculus and others already have delivered discrete and elementary metric schemes and the first one is here mentioned again in section 5, considering the strength of its non-local, non a priori time oriented, three-dimensional (or 3-valent) ground, therefore bringing elements fitted for the model hereunder considered. Recall also that in dimensions 2 and 3 here considered the Ricci tensor defines the full curvature tensor.

The extension of the ‘Yes/Noʼ structure to gravitation is experimentally problematic considering that the gravitational interaction is about 10⁴⁰ weaker than the electromagnetic, but is indirectly envisaged by [12] about the quantum entanglement ‘Objective Reductionʼ issue and appears directly to drive to the sort of SATisfiability formulation presented below. Now the gravitational field equation involves both Ricci and scalar curvatures and a piece of literature has been devoted to building metrics with given curvature and related topologies: sectional, Ricci and scalar curvature are considered about having constant sign [29] for sectional as well as Ricci, with then a focus on the Ricci case and Ricci flow. Negative Ricci curvature for instance is shown [30, 31] to be framed or even constant and admitted by any 3-dimensional manifold, whether open or closed. Positive Ricci curvature was also shown (Kobayashi, Perelman, Simon, ...) to result in homogenizing curvature but in a restricted choice of topologies. It is therefore legitimate to take for the random k-SAT x_i the R^± given by random elementary Ric(eⁱ ,eⁱ ) = ±1. Recall also the orthogonal basis functions of spherical harmonics for Legendre polynomials as elementary pieces of information which, for gravity, are appropriately about elements of curvature. Complementary issues about defining these basic elements of curvature are discussed in section 5 and concluded in section 6.

Furthermore a unique global topology is not directly implied from the FLRW hypotheses extending General Relativity to the universe as a whole, even though time orientation and isotropy for instance, preserving the full group of isometries, much restrict the choice after Thurston (geometries) or as Bianchi types. Topological uniqueness and related geometrical implications are not mandatory and the Hartle-Hawking model [11] model, cf. the preamble, mixes co-evolving Euclidean and Lorentzian sets of metrics and regions, yet driving the both through a comprehensive system of diversified metrics within their original Feynman path integral adaptation to gravity.

Finally, before testing the model itself a few more remarks about usual but not mandatory assumptions are needed. Flatness is considered primarily to result from preservation of a unique critical energy density ratio, itself ensured by a then growing dark energy or more natural cosmological constant Λ effect compensating the dilution of some a priori given mass and radiation budget. The ΛCDM arguably then appears to require less improbable construction than an artificial dark energy. Still, the natural evolution of SATisfiable versus nonSATisfiable universe metric and topological quanta (hence non-infinitesimal) formulated below seems naturally to ensure and conserve flatness while resulting in the latest universe observed, cf. next section.

In summary the Uni-SAT model takes the N random variables as quantized elements of local metrics each endowed with a bit of positive or negative curvature, from initial pairs out of ‘nothingʼ hence reduced to the classically normalized k = ±1. Potential assignments grow exponentially⁵ with N to a maximum of interchangeable, equivalent configurations in a global Euclidean topology but from a distribution of locally ⁵ Mézard [10] recalls that the set of random k-SAT configurations “typically scales like exp(Nα)”, this exponential growth being itself part of the power of the Non-deterministic, NP problems or languages complexity level. either spherical (+1, +1, +1) or non-spherical (with at least one negative bit of curvature) clauses as topological components. One may comment that topology, although born from Poincaréʼs “Analysis situ”, is rather global but in a quantum gravity perspective this may precisely be the sort of consistency, at some global level and object (cf. discussion and conclusion) then called a region or a universe, given by a set of commonly SATisfiable such clauses. Or conversely to which a global topology may be reduced, i.e. with loops able to be shrunk to such minimal loops or spheres in the spherical case or unclosed pieces of space otherwise.

As a result, SATisfied versus UNSATisfied regimes are ascribed to repulsive versus attractive regions. Expansion particularly departs from FLRW as the ratio from the lot of repulsive regions (voids) stall at the SATisfiability threshold α, as more precisely discussed below.

A local formulation of the splitting immediately resulting from the SAT versus UNSAT parts gives:

Φ_u = SAT [(x₁₁ ∨ x₁₂ ∨ x₁₃) ∧ ... ∧ (x_n1 ∨ x_n2 ∨ x_n3)] ∧ UNSAT {[(x₁₁ ∨ x₁₂ ∨ x₁₃) ∧ ... ∧ (x_n1 ∨ x_n2 ∨ x_n3)] ∨ A_q (x_r1,.... , x_rn)} (3)

where:

- so-called ‘violatedʼ clauses are here ascribed to positive metrics as (+1, +1, +1), i.e. when none of the three variables may be accepted as negative bit of curvature: they require additional oracle⁶ to bring them local closure, hence then solve their otherwise UNSAT contribution to the formula;

- SAT versus UNSAT therefore respectively embed regions of hyperbolic versus spherical topologies. The set of SATisfied clauses may evolve to cluster as the open hyperbolic part of the universe.

As previously mentioned Mézard [10] exhibits an evolution with a first clustering, out of a unique 1-state, into a split mixed set of states or clusters beyond the first, EASY to HARD threshold α_d and then finally all states or clusters of E > 0 after another threshold α_c. The difference here is that energy is rather interpreted as negative for exponentially expanding voids as opposed to the UNSAT part associated to the spherical, positively curved cells. Terms such as ‘violatedʼ and even SAT versus UNSAT may seem inappropriate in Physics, where events are rather said either to occur or not, but are useful for the link with the results achieved in Computational Complexity. Therefore the assignment of SAT to non-positive as opposed to UNSAT to strictly positive spatial metric is a bit arbitrary but is explained below from the topological differences between the both.

Recent further topological restrictions for positive curvature are summarized and concluded in [36]. Meanwhile a series of theorems in Complexity theory also relate graphs, context-sensitive languages, order levels and transitive closure with computational space, cf. preamble. Negative Ricci curved conversely donʼt entail topological restrictions cf. [18, 29, 30, 31] (again, justifying the assignment of violated clauses to positive curvature). From a quantum of Ricci curvature assumed constant and measured from some of the three basis vectors as Ric(eⁱ , eⁱ ) one gets a spread of volume with Euclidean volume either expanding (if negative) or shrinking (if positive).

The SAT component does not require, at least at this level, a boundary from which to ‘Acceptʼ its variables (in Computational language) or to ‘observeʼ (or ‘Achieveʼ) them (in Physical terms): it naturally develops globally hyperbolic open space(s). Conversely the UNSAT part requires, for consistency, the relativization provided by additional A_q(x_r1,.... , x_rn), environmental or oracle or also integration term, physically interpreted as its closure or compactness, set of all observersʼ points: this replaces the SATisfiability that they did not achieve, in the cosmological case as an attractive portion of the gravitational field.

It could be discussed whether to keep the AND (∧) before the UNSAT side – assumed from the present model to encompass the attractive, so-called Dark Matter side of our universe – or to turn it to an OR (∨) as then keeping outside to the observer at infinity or to ourselves the common oracle then defining the both as a common universe, while enabling this UNSAT as a, once closed, complementary SAT part, but become spatially separated (OR). In other words the splitting of (1) and (2) would result in the splitting in clusters or regions of the universe, negatively versus positively curved, represented by (3) with both parts only differently, i.e. topologically SATisfied.

The model here sketched may have additional implications. For instance for the well-known questions of the emergence of small inhomogeneities, even from quantum gravity cf. e.g.[37], as well as the issue of the initial asymmetries in the universe (such as matter vs. antimatter), that a SAT versus UNSAT generalized formula conversely systematically entails.

The choice could be made above in Φ_u to keep A_i, although unneeded a complement to the SATisfied cluster as opposed to the necessary Aq for UNSAT. These oracles, then providing the negative, time-like resolving complement, may also be considered as the time boundary for this part, carrying the entropic potential as a physical measure of the oracle set. The spatial expansion of the negatively curved side particularly exhibited in cosmic voids appears then untimely or infinite as opposed to the positively curved, for which time frontiers engage ever more complexity steps.

The question of universal global time is highlighted by e.g. [38] about the Wheeler–de Witt equation, but then related to providing a horizon, if only to the spherical part cf. [39]. Also, observationally the issue, recalled at the beginning of this paper about customary R x M³ topology, whereby the universe is assumed to keep a given topology for a three-dimensional section remaining homogeneous along most of its history and at least at large scale, is to the best of our knowledge not settled at this time⁷.

Extension of SATisfiability beyond the gravitational field

A consequence of the formula is that a typical 3-SAT clustering [10, 16, 17, 20] hence translates, as applied to this Uni-SAT cosmological model, in severing cosmic voids, the negatively curved SATisfied part, from domain walls and the attractive dark matter resulting from the UNSAT positive curvature micro-domains progressively themselves evolved into macro-domains or halos.

The behavior modeled and simulated by [10, 16, 17, 19, 20] of a clustering of the SAT in easy-SAT before hard-SAT regimes, invites a generalization, expressed with a compact simplified formula as:

Φ_U = SAT [∧_i=1^M (∨_j=1^k a_ij)] ∧ [U_q UNSAT ∧_i=1^M (∨_j=1^k a_ij) ∨ A_q (x_r1,.... , x_rn)] (4)

How may this already be here briefly interpreted? Φ_u first presents itself as a formula for a genuine or void universal gravitational field, that a logical universal SATisfiability for consistency requirement naturally splits between the SATisfiable hence open, asymptotic hyperbolic part and the UNSAT spherical, which requires closure to get SATisfied, such as considered by [11] with S³ topology, where a split between compact and open regions is also debated.

Then, and somehow in the spirit of a jump, in [15], from the customary gravitational universe u to a comprehensive U, Φ_U tentatively sketches how the splitting repeats, within the primarily UNSAT part of Φ_u, where closure generates enhanced complexity, to begin with a transition from this positive curvature interpreted as dark matter into baryonic matter.

4. Observational Results

Three separate streams of mostly recently published experimental results are relevant for this Uni-SAT(u) model:

i- From Complexity theory, observations and simulations of the thresholds separating SATisfiable from UNSATisfiable regimes;

ii- From Cosmology, simulations and measurements of the Hubble parameter from mainly early, high-redshift CMB [5] versus late, low-redshift Supernovae 1a observations [23];

iii- From Astrophysics, about voids and halos.

Series of observations about sphere staking phenomena from Computational complexity The first series has approached a value of the αd threshold toward an intriguing ‘clusteringʼ phase transition by [19] to 3.927 ± 0.004 for k = 3, reevaluated at αd = 3.86 later by [16]. Switching from α = M/N to a probability ratio β = 1 – 1/α, with α in [1, +∞[, quantifies chances to find a set of clauses SATisfied by the variables, versus the probability of SATisfying the configuration: at least a huge number of clauses gives α >> 1 and β → 1 but a complementary discussion, about what β may represent, is required and takes place below as a consequence of observations that α_d = 3.86 converts into β_d ≅ 0.7409, very close to π/√18 ≅ 0.7405, the Hales-Kepler limit ratio of a 3D stacking of spheres. It may be added that K-COL problems, coloring of graphs so that no edges link vertices with the same color, undergoes processes, behavior and complexity classification similar to K-SAT, with the case of random 3-COL where α is defined as 2E/N (instead of M/N), E being the number of edges and N of vertices cf. [47] exhibits a first phase transition observed at cL ≅ 3.847, which would translate into β_L ≅ 0.74006, framing a little more the suggested exact Hales-Kepler value of π/√18. Monasson refers in [47] to previous works with S. Cocco where the Davis-Putnam-Logemann-Loveland (DPLL) procedure was applied to random K-SAT.

Diverse other kinds of potential applications in Cosmology and Physics would seem worth pursuing but exceed the focus of the present paper. Monasson mentions some cases such as generalization to search trees where edges represent logically (i.e.) linked, hence satisfied constraints from a random assignment of variables to the vertices. Then Krzakala et al. [17] recall the result of Montanari et al. of α_d(3) = 3.86 but emphasize that “a rigorous calculation” of this threshold “along any of the two definitions provided above (…) remains an open problem”. Could, however, this threshold be proven derivable from the exact Hales-Kepler value as β_d → π/√18, which may at first look like one of the mere coincidences not unheard of in Physics? This becomes of interest because aforementioned papers model the phase transition with a clustering into a jamming of ‘Hard spheresʼ [20], and such sphere stacking throughout Euclidean cubic lattice being a limit previously proposed [22] for the ratio known as ΩΛ. Now the β derived from the clause density ratio α = M/N, conversely suggests that the breaking over the limit β_d = π/√18 is precisely at α_d = 1/(1-π/√18) and corresponds to the ratio of satisfied clauses which in that case are sheer, unbounded space quanta with elementary local hyperbolic topology. More precisely in the present proposal, where the N variables are genuine bits of space, the phase transition is achieved when both the open SATisfied regions interpreted as repulsive, and the UNSAT closed (and then become SATisfied) interpreted as attractive, all reach their entropic capacity within optimal space configuration, such as increasingly well observed and computationally simulated… at this point where infinite differentiability is modeled and computed.

The resulting picture is a kind of Voronoi tessellation and diagram, for which a rich literature accumulates, cf. [9] for a diversity of Voronoi distance metrics and also [48], where the Voronoi diagrams are considered within a hyperbolic geometry of constant K = - 1/r² negative sectional curvature and through five usual models (Klein, Poincaré Ball and Upper, Hyperboloid, Beltrami). Their purpose is however usually geared toward computational complexity efficiency. In the present tentative application to the cosmological consistency issue the distance metrics are locally determined according to General Relativity requirements, as proposed in the previous section, meaning primarily by quantized Ricci curvature since neither matter nor any energy other than gravitational, in fact assumed primarily ground state flat Euclidean, are assumed as yet. But then it may be recalled that General Relativity equations themselves derive from universal consistency postulates, to begin with general 1+3 covariance about which [7] require the “consistency of the constraints with the evolution equations” to frame the “set of all cosmological solutions” that fit with observations. This “‘fullʼ state space of solutions” of interest to Ellis-van Elst is therefore the set of Acceptable or Satisfiable solutions, which may be interpreted as its oracle, for which Hartle-Hawking propose the applied role of their Wave function. From the Uni-SAT formulation (3), the set of negative curvature, or non-positive – i.e. non - (+1, +1, +1) – of subsets of clauses, or their related manifolds, is constrained under β_d for their volume, hence energy ratio. But then what about the non-satisfying or UNSAT other subsets? On the one hand they carry the balance of curvature within regions with spatial spherical topology but acceptable and fourdimensional Lorentzian within a common complementary negative timelike dimension giving its (+, +, +, -) usual signature.

Series of observations and measurements of the Hubble parameter

In the second series, Bernal, Verde & Riess [23] model a reconstructed Hrecon function remaining constant from redshift z ≅ 0.2 to Now (z = 0). They notoriously wonder about the source of the well-known and critical persistent divergence, over the previous decade, between at least two types of measurements of the Hubble parameter H(z) or even Hubble constant H₀ (at z = 0, when derivable from H(z)):

i) High-redshift, CMB based and from there ΛCDM inferred Hubble constant H₀, calculated, using the Friedmann equations at circa 67 km/s/Mpc, cf. e.g. [5];

ii) More direct measurements, e.g [6], based upon relatively ‘localʼ observations of Type Ia Supernovae, meaning for z < 0.6 and, depending references, even much lower z, then giving an estimated H₀ ≅ 73 km/s/Mpc.

In their 2016 paper the authors [23] survey two types of sources for the divergence, hypothesizing unknown effects either occurring at high redshift and that they label “changing early-time Physics” or very recent, i.e. at low redshift and coined “changing late-time cosmology”. For this second series of possibilities they recall that “H(z) is monotonically increasing with redshift” in a ΛCDM model, while several observational sets suggests that H(z) could be only slightly increasing or even constant at very low z (below 0.2 or even closer to ‘usʼ). More precisely they emphasize that the “shape of the expansion history” remains nearly that predicted by ΛCDM (even) at z < 0.6, so that the “sharp increase in the cosmic acceleration rate”, with H(z) nearly constant, would indeed be much more recent.

Now recall that the cosmological constant Λ “satisfies the relation ∇_a Λ = 0”, meaning that it is “constant in time and space” [7]. In other words it find its inner satisfiability with neither boundaries in space nor in time, which is what the repulsive, or at least negatively curved, in fact non-spherically constrained, ‘SATʼ first part of Φ_u entails.

This component is interpreted as repulsive relatively to its attractive pendant then interpreted as Dark Matter but the main point is that it carries the expansion naturally borne from random N → ∞. Two questions then arise:

- How would this result in the ‘late lateʼ acceleration modeled by an H(z) = constant;

- Why so close to us, to Now, a question known as the cosmological coincidence.

A de Sitter expansion already ‘Nowʼ

Constancy of H(z) is known to be related to a de Sitter exponential expansion since H(z) is defined as ȧ/a where ȧ is the time derivative of the scale factor a, so that it implies that a ≈ e^Ht, and recall that the exponential expansion is associated to the NP-complete 3-SAT complexity growth of the number of configurations as exp(N^α).

The point here is that this de Sitter equivalent expansion ‘already nowʼ may derive from the SAT threshold: the interpretation, from the Uni-SAT model, is that the flow of new variables remains constrained by this threshold to keep the clustering having now well separated the dominant set of largest cosmic voids (the SAT subset or regions), hence appear as a de Sitter expansion while more complex phenomena (including black holes) occur in the UNSAT, aka dark matter spatially complementary subset.

In other words the de Sitter expansion is mostly carried by the set of now well formed cosmic voids, eligible to carry, spread among themselves, the de Sitter behavior typically associated to void universes or, presently, regions jamming the otherwise Euclidean, i.e. on average flat universe. The third set of observations herein referred to, below, appears to concur about such an evolution.

The coincidence is conversely rather answered by the other side of the formula, which undergoes its own kind of exponential expansion, but this one turned toward densification into ever newer more complex objects which, for the case limited to the gravitational phenomenon, end in Black Holes.

Here is the quest for which weak to strong Anthropic principles propose their solutions but a whole literature has also been devoted to the exponential acceleration of complexity resulting in… ‘usʼ, currently at least the observers, modelers and debaters about cosmological models up to our ‘Nowʼ.

Series of observations and measurements about the behavior of Cosmic voids

The third series describe the behavior, shapes and sizes of major cosmic voids [24, 25, 26, 27] and [28] presents a partition of ‘separate universesʼ as positive curvature, attractive spherical, versus negative curvature, repulsive hyperbolic regions. Wojtak, Powell and Abel [24] for instance develop an approach discretizing voids as “sets of pixels in space rather than a set of particles”, toward a density field “well-defined everywhere in configuration space”. They also conclude from observations and numerical simulations that these largest voids exhibit “larger core, weaker walls and a sharper transition between the core and the boundaries”, later even emphasizing a “theoretically bucket-like shape of the final density-profile” of these largest cosmic voids.

More drastically Jamieson & Loverde [28] even precisely talk of separate universes, that is to say a split between hyperbolic universes with a small negative curvature playing the role of Dark Energy as repulsive voids, versus positively curved regions playing as Dark Matter. It is noteworthy that Sutter et al. [24] observe that the “interior” of “larger voids” look like “miniature open universes”.

In short, observations from three separate fields (Statistical physics about SATisfiability, Astrophysics about voids and Cosmology about the Hubble parameter and enduring flatness) appear to concur on separated and complementary roles roughly summarized as a repulsive set or system of spherical cosmic voids versus the attractive, dark matter set, with the first already now driving an overall equivalent de Sitter expansion; all this awaiting more precise estimates of H(z). The split amongst opposite regions, with the then hypothesized resulting role of ΩΛ determined for ‘Nowʼ by the π/√18 sphere packing threshold, was previously proposed in [22] and references herein.

5. Discussion

The expansion and structuring of a “quasi-FLRW universe” [7] are quite precisely modeled and numerically simulated in Cosmology, after a Big Bang however neither that Big nor that Bang and the quantum gravity model proposes by HartleHawking starts from a “single point” and then obey a Feynman path integral of all compact four-geometries bounded by some starting and ending three-geometry, opening questions such as:

i) How do the three geometries themselves arise, especially with the compelling difference between negatively and positively curved geometries both proven to evolve in finite time toward respectively constant negative or constant positive curvature?

ii) How does this impact the acceptable four-geometries? A quantum ‘single pointʼ is here envisaged a ‘naturalʼ ground-state emergence of pair of space metric bits of opposite quantum of curvature, which might then be even interpreted as gravitational particle pair for the related field.

The question of a lowest initial number of degrees of freedom, say with only one and then two spatial dimensions, becomes in order: the curvature with two-dimensional spaces, or surfaces, is simpler, following Gauss-Bonnet theorem. It is even reduced in one dimension to zero, most basic flatness, for the straight line of electromagnetic phenomenon corresponding to the single spatial dimensionality. The two-dimensional phase may be envisaged to follow a Polynomial Time 2-SAT process while the transition to three-geometries opened the entropic exponential growth associated to 3-SAT, which might in turn be interpreted as inflation, although with no time clearly definable as yet since the SATisfiable part, initially 100% (easy) does not require a four-dimensional term: time.

Dimensionality, entropy and the transition from 2-SAT to 3-SAT

This links to Complexity theory, where random 3-SAT is the NP-complete level jump from 2-SAT, simpler P level. The gap is here linked to the transition from spatial 2 to 3 dimensionality and its relativized [14, 40] extension to four-dimensional space-time. The fourth dimension aggregates the environment as oracle, through the time function naturally maximizing entropy. The oracle, customary in Computational Complexity as the set encompassing acceptance of a logical content, hence binds and bounds (our A_q in (3)) as the ‘Rʼ of R x S³ , the Cauchy surfaces of Dark Matter halos, from where these observersʼ sets, Gerochʼs points, use their terminal clocks and time units.

While [32] models a lattice where opposite attractive matter versus repulsive antimatter is assumed to account for the role of a dark energy, the lattice approach of [22], as a different angle or approach to the very model here presented, did not assume any antimatter. The asymmetry between SATisfiable as open, repulsive hyperbolic sets finally concentrating as cosmic voids versus UNSATisfiable regime interpreted to concentrate into so-called dark matter halos, appears sufficient to generate otherwise so-called ‘Spontaneousʼ symmetry-breakings, as discussed below. About this last point may be mentioned an idea of dark energy and curvature from ongoing particle creation, traced backward by [33] to Zeldovich, while [34] recalls the development of f(R) gravity modeling dark energy and dark matter as resulting from curvature effects related to the modified Lagrangian. As compared to both streams, the present model of sheer quantized space creation, with manifold structure and topologies as consequences and underlying all more complex phenomena, appears to keep things maximally simple under the sole assumption of global consistency and the second law, itself expressing Statistics (the Non-deterministic probability of the SATisfied future is nearly one). It may be conjectured that the 2-SAT to 3-SAT growth in complexity, and related dimensionality jump, contributed in its own right. Only four-dimensional manifolds are infinitely differentiable⁸, cf. [41] after which a development integrating knot theory is presented by [42] but discussing a relationship with it requires complementary papers. Recall also the “toy model” of [35] mentioned in the preamble in dimension 2 that appears all the more meaningful in the SAT perspective here presented and with the hypothesized manner of dimensionality growth.

A complement about entropy: the random 3-SAT formulae apply to Configuration sets or spaces scaling as exp(N^α) as previously mentioned after e.g. Mézard [10]. The related phase space in Cosmology however splits between the entropy maximized by the intrinsic (negatively curved) SAT subset or subspace and the additional entropy of the fourdimensional positively curved subset. Estimates are provided by e.g. Penrose, Carroll, especially for this complementary subset, where local maxima are reached in the gigantic Black Holes at the centers of galaxies, where the number of possible equivalent, interchangeable configurations, culminates at the S_BH ≈ A/4 value.

Similarly the entropy born by the cosmic voids culminates once their own spherical shapes and emptiness render configurations maximally equivalent. But then the fate of these cosmic voids is merely a radial expansion at exponential de Sitter rate while Black Holes, also expanding in radius by swallowing neighboring matter, are nevertheless constrained by the greater entropy growth requirement of the whole UNSAT system of configurations.

Symmetry-breaking

‘Spontaneousʼ symmetry-breakings in earliest cosmology are an issue but the apparent symmetry of the (+1, +1, +1), (+1, +1, -1), (+1, -1, -1) and (-1, -1, -1) becomes dissymmetry when space own dimensionality and related complexity are involved. About this complexity, an equivalence between Rational graphs and CSL languages was mentioned in the preamble. Two other relationships about Closure and Order levels through Formal Languages Complexity classes, with then equivalences in Configuration spaces, are recalled here from Immermann [53]:

CSL ⇔ (FO + positive TC) ⇔ NL (Non-deterministic LOGSPACE)

Where FO is First Order Logic, TC ‘Transitive Closureʼ and CSL Context-Sensitive Languages

(SO + TC) ⇔ PSPACE (= NSPACE)

Where SO is Second Order Logic and PSPACE the class of languages, or problems that require access to deterministic space polynomial of input size, while NSPACE is Non-deterministic Space.

Only these relationships are mentioned here to exhibit the role played by closure, which is where the dissymmetry between open sets or regions (intrinsically SATisfied) versus closed (needing an oracle able to bring acceptance) yields a natural dissymmetry possibly resulting in compactification.

Inhomogeneous, distributed ‘Large Scale Structureʼ

Finally, the most simple process here synthetically modeled appears to account for an ongoing flat expansion along which negatively and positively curved regions progressively sever to deliver the recent Large Scale Structure known to be algorithmically well simulated: it is noteworthy that the requirement of entropy growth and maximization should preempt, as the most global and dominant constraint and primary cause, hence randomness, usual global assumptions, here consequential, added to General Relativity to build cosmological models.

The Large Scale Structure increasingly well observed and computationally simulated appears to exhibit such a split between the set of open expanding cosmic voids getting increasingly well shaped, devoid and separated and the halos and clusters of dark matter concentrated systems of galaxies with even the maximally curved centers as gigantic Black Holes closing within their event horizons all what, conversely to opposite spatial expansion of voids, is here swallowed.

6. Conclusion

The conclusion is divided in two parts:

i) Immediate, refutable consequences for cosmological problems and more precisely parameters;

ii) Directions of research and complementary assumptions investigated but requiring further, dedicated work and formulation. In his section “Quantum Cosmology” of [11], Hawking summarizes fundamental cosmological problems, presenting some drawbacks of the ‘Hot Big Bangʼ model and adding that “inflation alone cannot explain the present state of the universe”, yet recalling that a slightly greater (“one part in 1010”) or similarly smaller rate of expansion would have resulted in a universe fast becoming empty or conversely collapsing. This comes immediately after his statements and proposal about a de Sitter model, created from nothing rather than “out of field energy in a preexisting space” and, even more, after comparing the birth of such a universe with a case of pair creation of black holes.

Probabilities about a nascent universe, starting from some space presumably minimally dimensioned, hence even not yet gravitational field, may themselves only be hypothetical, depending some a priori assumptions and model. For instance a universe starting from nothing, with no a priori given space, might start from one spatial dimensional, thereby limited to radiation energy field and era, gravitational field only surging with curvature from space getting to two and then three-dimensionality. Only then would departing from flatness, isotropy and homogeneity become possible through quantum fluctuations of the field but under which overall constraint? In other words what basically constrains a gravitational field starting from nothing, hence null with no reasons to depart from flatness although the ongoing creation of quantized pairs of what may be interpreted as curvature versus anti-curvature, result in already known split voids versus halos.

i) Testable consequences

A conclusion allowed by Uni-SAT model is that the evolution of the cosmological parameters are a consequence rather than a cause of the flatness of the universe, which is the anchor within which regions of positive versus negative curvature progressively sever from one another toward the lately observed Large Scale Structure where spherical cosmic voids expand, tend to occupy maximal three-dimensional space and constrain the attractive regions to the observed filaments and nodes, these attractive halos roughly tending to fill the space left by the stacking of spherical voids.

The behavior of this void set of the universe then drives the overall spatial expansion of the universe, which behavior therefore looks like a de Sitter one. It is noteworthy that Bernal, Verde and Riess have in [23] hypothesized, from their observational results, a constancy of the Hubble parameters since z < 0.2 which would, if strengthened by incoming observational data, support the Uni-SAT perspective. This would also depend on increased precision in the cosmological parameters without prior model, if they were to confirm the sort of cosmological ‘phase transitionʼ by then, that is to say for instance circa z ≅ 0.2 reached with a repulsive energy density ratio (commonly meant as ΩΛ) then reaching the value of π/√18.

The difficult reconstitution, through improved and diversified streams of observations and simulations, as much as possible model independent, of the evolution of H(z) since roughly z < 1, is the current gigantic task mobilizing the efforts of astrophysicists so that it can be expected that the figures of the gravitational universe transition here envisaged may be refuted or not in this decade.

ii) Other potential impacts and directions of complementary work

The ‘narrowʼ, strictly gravitational or Uni-SAT(u) model appears to bring a novel way to answer the flatness problem but the coincidence problem remains. This is where, arguably in a still more conjectural manner, an extension of the SATisfiability requirement is sketched with the tentative UniSAT(U) generalization, itself derived from the overall logical consistency expectation of scientific knowledge. Toward such a goal is recalled above Ellis & van Elstʼs “set of all cosmological solutions” but then here as ‘set of all (consistently) SATisfiableʼ such solutions, about or rather within which Dowker & Kent [54], being concerned with the number of ‘consistent historiesʼ in their set S, “look favorably on any natural criterion which reduces the number of sets”, adding that “only consistent sets (are) of physical relevance”, yet with “associated times to define the history”.

The question comes of the next ‘timeʼ defining such next level of history consistency requirement although, to their expectation of dual consistency and completeness Girardʼs comment opposed Gödel. This conclusion is not the place to discuss the related series of intermediate times t_j of projections, measurements of “sequences of events in time (…) which satisfy the conditions” (of sets of orthogonal hermitian projections summing to one) from which any “set of alternatives S” results. Observe however that these are assumed to happen within given four-dimensional spacetime(s) while, under similar consistency requirement to physical relevance, the Uni-SAT Φ(u) pertains to the very definition or possibly model of such a time ‘inʼ which sequence of events occur.

Time as dissymmetry from SATisfiability

What is time? As far as we know the dissymmetry defining time as opposed to space in the signature (-, +, +, +) and, at the other edge, from acceptable evolutions with the growth of entropy up to some capacity of some coarse graining, so far appeared at odds with the time symmetry, the reversibility of the laws modeling physical phenomena through series of events. Dowker & Kent introduce their paper with the remark that the standard Copenhagen interpretation “cannot be applied to closed systems” but there comes the question of what closes a gravitational system, or universe, presumably a boundary from where the system is closed as consistent if SATisfiable, from its content. To this term such closure, or a Turingʼs oracle in Complexity theory, may turn some UNSAT enclosed field as consistent since SATisfied, starting from this closing timelike coordinate of the 3 + 1 covariance underlying General Relativity, then requiring further completeness. Resulting sequences of events thereby acquire this ‘physical relevanceʼ quoted above.

Generalization

Through the generalized Uni-SAT(U), it is envisaged, but would require dedicated and explicit work, that the related next major phase transitions, thereby each unfold at a next exponential speed, or timeframe, giving the impression of terminating in the ‘Nowʼ from where, it is a fact, they are theorized, observed and computed. Considering that the exponential has no asymptote it may however be estimated that all these ‘nowsʼ will still last some time. At least until the last axiom (though Girard warns there is always a next one) may come with Barrow & Tiplerʼs “Ultimate observer” or Dowker & Kentʼs ultimate IGUS, hence the induced question of whether Humanity will reach such expected, unified, valid and consistent, SATisfying knowledge in finite time or not. While Φ(u) is proposed as precise mechanism preserving ground-state flatness, Φ(U) is rather meant as a sketch applying the SAT/UNSAT dissymmetry to next physical order levels through their specific phase transitions, which may start as soon as elementary particles and baryogenesis. Each however depend on what closes each underlying UNSAT order level and thereby defines the variables of the next one, starting from the four-dimensional metrics with their added, timelike, bits of negative contributions toward, then, Minkowski space. Transitions with symmetry-breaking have multiplied and become a complex landscape since the electroweak one, and yet the requirement of overall consistency, for a universe nevertheless never fully SATisfied, i.e. both complete and consistent, therefore will long keep us looking for the missing “next axiom(s)”.

Acknowledgements

The author thanks John Madore for his early encouragements, and furthermore Marc Lachièze-Rey for his enduring support.

¹We highlight in bold here the tight mathematical requirement implied by these words. Meanwhile Hartle-Hawing also emphasize the ‘all possibilities’ aspect in the last section of their paper.

²A Non-deterministic Turing machine (NTM) is assumed to actualize randomness: a solution or configuration is guessed (taken at random i.e token thrown) and then tested through a deterministic ‘Verifier’ as logical computing. Hence a dual machine with exponential power on one side (the Prover) and polynomial for the Verifier. Differences with the Oracle Turing Machines cannot be debated here.

³Obviously the more constraints or clauses M are fed in a consistency requirement the less easily SATisfiable it will be, but the discovery of a threshold from easy to hard SAT and then UNSAT depending only on their ratio was unexpected.

⁴The assignment to Yes/No seems more arbitrary in Physics, often corresponding to phenomena of opposite sign (up/down, matter/antimatter), than in Mathematics and furthermore in Logic. The ground for the assignment of negative curvature to Yes and positive to No and relationship with time is explained in the second part of this section.

⁵Mézard [10] recalls that the set of random k-SAT configurations “typically scales like exp(N^α)”, this exponential growth being itself part of the power of the Non-deterministic, NP problems or languages complexity level.

⁶Which allows SATisfiability by introducing a negative (-1), allowing Lorentzian signature (+, +, +, -), again as time.

⁷The author of the present paper heard Jean-Philippe Uzan have a concluding talk of COSMO 11 in Porto and the year after Andrew Stebbins at another concluding talk of Cosmo 12 in Beijing, both emphasize the same issue.

⁸Also, a variable, say xi1, may be seen as set of (xi₁ ∨ xi₂ ∨ xi₃) ∧ (xi₁ ∨ xi₂ ∨ xi₃) ∧ (xi₁ ∨ xi₂ ∨ xi₃) ∧ (xi₁ ∨ xi₂ ∨ xi₃), hence common boundary, oracle or term of all these fourfold formulae with compensated other spatial dimensions

References

1. Hawking S, Ellis G. The Large Scale Structure of Space-time. Cambridge University Press; 1973. 2.   
2. Hawking S, Penrose R. The Nature of Space and Time. Princeton University Press; 1996.   
3. Carroll S. The Cosmological Constant. Living reviews in relativity. 2001; 4(1). doi: 10.12942/lrr-2001-1   
4. Hinshaw G. et al. Nine-year Wilkinson Microwave Anistropy Probe (WMAP) Observations: Cosmological Parameter results. arXiv. 2013; doi: 10.48550/arXiv.1212.5226   
5. Planck collaboration. Planck 2018 results VI. Cosmological parameters. arXiv. 2018; doi: 10.48550/arXiv.1807.06209   
6. Riess A, Marci LM, Hoffmann SL, Scolnic D, Casertano S, Filippenko AV, et al. A 2.4 % determination of the Local value of the Hubble constant. ArXiv. 2016; doi: 10.48550/arXiv.1604.01424   
7. Ellis G, Van Elst H. Cosmological models (Cargèse Lectures 1998). arXiv. 2008; doi: 10.48550/arXiv.gr-qc/9812046   
8. Cook S. The Complexity of Theorem Proving Procedures. Proceedings of the 3rd ACM Symposium on Theory of Computing, New York. 1971.   
9. Boissonnat JD, Karavelas M. On the combinatorial complexity of Euclidean Voronoi cells and convex hulls of d-dimensional spheres. INRIA. 2003.   
10. Mézard M. Optimization and Physics: On the Satisfiability of Random Boolean Formulae. arXiv. 2002; doi: 10.48550/arXiv.cond-mat/0212448   
11. Hartle J, Hawking S. Wave function of the universe. Phys Review D. 1983; 28(12). doi: 10.1103/PhysRevD.28.2960   
12. Penrose R. The Road to Reality, A. E. Knopf, New York. 2004.   
13. Larrabee T, Tsuji Y. Evidence for a Satisfiability Threshold for Random 3CNF Formulas. Baskin center for Computer engineering and Information Sciences, U.C. Santa Cruz. 1992.   
14. Fortnow L. The Role of Relativization in Complexity Theory. University of Chicago. 1993.   
15. Barrow J, Tipler F. The Anthropic Cosmological Principle. Oxford U Press, New York. 1986.   
16. Montanari A, Ricci-Tersenghi F, Semerjian G. Clusters of solutions and replica symmetry breaking in random k-satisfiability. arXiv. 2008; doi: 10.48550/arXiv.0802.3627   
17. Krzkala F, Montanari A, Ricci-Tersenghi F, Semerjian G, Zdeborova L. Gibbs states and the set of solutions of random constraint satisfaction problems. PNAS. 2006; doi: 10.48550/arXiv.cond-mat/0612365   
18. Lachièze-Rey M, Luminet JP. Cosmic Topology. arXiv. 2003. doi: 10.48550/arXiv.gr-qc/9605010   
19. Mertens S, Mézard M, Zecchina R. Threshold Values of Random K-SAT from the Cavity Method. Wiley InterScience. 2004. doi: 10.1002/rsa.20090   
20. Mézard M, Parisi G, Tarzia M, Zamponi F. On the solution of a solvable model of an ideal glass of hard spheres displaying a jamming transition. J Stat Mech. 2011; P03002.   
21. DʼArcy Kenworthy W, Scolinic D, Riess A. The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant. arXiv. 2019; doi: 10.48550/arXiv.1901.08681   
22. Journeau P. New Concepts of Dimensions and Consequences. CP1018, Frontiers of Fundamental and Computations Physics, American Institute of Physics. 2008.   
23. Bernal J, Verde L, Riess A. The Trouble with H₀. arXiv. 2016; doi: 10.48550/arXiv.1607.05617   
24. Wojtak R, Powell D, Abel T. Voids in cosmological simulations over cosmic time. arXiv. 2016. doi: 10.48550/arXiv.1602.08541   
25. Hamaus N, Sutter P, Wandelt B. Universal Density Profile for Cosmic Voids. arXiv. 2014. doi: 10.48550/arXiv.1403.5499   
26. Hamaus N, Pisani A, Sutter P, Lavaux G, Escoffier S, Wandelt B, Weller J. Constraints on cosmology and gravity from the dynamics of voids. arXiv. 2016; doi: 10.48550/arXiv.1602.01784   
27. Sutter P, Elahi P, Falck B, Onions J, Hamaus N, Knebe A, Srisawat C, Schneider A. The life and death of cosmic voids. arXiv. 2014; doi: 10.48550/arXiv.1403.7525   
28. Jamieson D, Loverde M. Separate Universe Void Bias. arXiv. 2019; doi: 10.48550/arXiv.1909.05313   
29. Leite M, Dotti de Miatello I. Metrics of Negative Ricci Curvature on SL (n, R) n³3, J. Differential Geometry. 1982; 17: 635-641.   
30. Brooks R. A Construction of metrics of Negative Ricci Curvature. J Differential Geometry. 1989; 29: 85-94.   
31. Lohkamp J. Negatively Ricci Curved Manifolds. Bulletin of the American Mathematical Society. 1992; 27(2).   
32. Villata M. On the nature of dark energy: the lattice Universe. Astrophys Space Sci. 2013; 345: 1-9. doi: 10.1007/s10509-013-1388-3   
33. Cardenas V. Dark energy, matter creation and curvature. Eur Phys J C. 2012; 72: 2149. doi: 10.1140/epjc/s10052-012-2149-0   
34. Capozziello S, Cardone V, Troisi A. Dark energy and dark matter as curvature effects. arXiv. 2006; doi: 10.48550/arXiv.astro-ph/0602349   
35. Loll R, Ambjørn J, Anagnostopoulos K. Making the gravitational path integral more Lorentzian or Life beyond Liouville gravity. Nucl Phys Proc Suppl. 2000; 88: 241-244. doi: 10.48550/arXiv.hep-th/9910232   
36. Simon M. Ricci flow of almost non-negatively curved three-manifolds. arXiv. 2018; doi: 10.48550/arXiv.math/0612095   
37. Padmanabhan T. Aspects of Gravitational Clustering. arXiv. 1999; doi: 10.48550/arXiv.astro-ph/9911374   
38. Linde A. Inflation, Quantum Cosmology and the Anthropic Principle. arXiv. 2003.   
39. Padmanabhan T. Classical and Quantum Thermodynamics of horizons in spherically symmetric spacetimes. arXiv. 2002; doi: 10.48550/arXiv.grqc/0204019   
40. Fortnow L. Time-Space Tradeoffs for Satisfiability. University of Chicago.   
41. Donaldson S. An application of gauge theory to the topology of four manifolds. J Diff Geom. 1983; 18: 269.   
42. Witten E. Quantum Field Theory and the Jones Polynomial. Commun Math Phys. 1989; 121: 351-399. doi: 10.1007/BF01217730   
43. Hawking S, King A, McCarthy P. A new topology for curved space-time which incorporates the causal, differential and conformal structures. Journal of Mathematical Physics. 1976; 17(2). doi: 10.1063/1.522874   
44. Freed D, Uhlenbeck K. Instantons and four-manifolds. Mathematical Sciences Research Institute publications. Springer-Verlag, NY. 1984.   
45. Nagel E, Newman J, Gödel K, Girard JY. Gödelʼs theorem (translated from ‘Le théorème de Gödelʼ). Girard JY. 1989.   
46. Hocroft J, Ullman J. Formal Languages and their Relation to Automata. Addison-Wesley. 1969.   
47. Monasson R. Towards an average-case analysis of backtrack procedures for random decision problems? ENS Paris. 2003.   
48. Nielsen F, Nock R. The hyperbolic Voronoi diagram in arbitrary dimension. arXiv. 2012. doi: 10.48550/arXiv.1210.8234   
49. Albrecht A, Sorbo L. Can the universe afford inflation? arXiv. 2004; doi: 10.48550/arXiv.hep-th/0405270   
50. Morvan C, Stirling C. Rational graphs trace context-sensitive languages. Lecture Notes in Computer Science Springer. 2001; 2136. doi: 10.1007/3-540-44683-4_48   
51. Monasson R, Zecchina R. Statistical Physics of the Random K-Satisfiability Problem 1998.   
52. Monasson R, Zecchina R. Entropy of the K-Satisfiability problem. Phys Rev Let. 1996; 76(21).   
53. Immermann N. Languages that capture complexity classes. SIAM J of Computing. 1987.   
54. Dowker F, Kent A. On the Consistent Histories Approach to Quantum Mechanics. arXiv. 1996.