Abstract

A model of the expansion of the universe is proposed, based on the assumption that the universe in its early stages was not in a hot state but in a pure, metastable quantum state. This assumption makes it possible to solve the basic paradoxes of standard cosmology from the unified positions and within the framework of the standard model, namely, the horizon problem, the flatness problem of the universe, the problem of the absence of monopoles, and the problem of the predominance of matter over antimatter.

Keywords: Flatness of the universe; Entanglement; Horizon; Decoherence; Baryogenesis; Superluminal communication.

Introduction

Currently, the early stages of the evolution of the universe are modeled both within the framework of inflation models and using other approaches. One of the basics for understanding the mechanisms of the expansion of the universe are its properties such as homogeneity, flatness and others. To solve these problems, an inflationary paradigm was proposed (see, for example, [1-5]), within the framework of which it is possible to solve some important problems of the expanding universe.

The problem of homogeneity (horizon problem) is that the temperature of microwave radiation differs only by a few hundred-thousandths in different directions. However, the size of the universe is too large for this homogeneity, since the removed parts of the universe could not be related to each other even at the speed of light, and thermalization faster than the speed of light is considered impossible. The second is the flat world problem. At present, the geometry of the universe is only slightly different from the Euclidean model. This imposes very strong limitations on the curvature of the universe in the early stages of its evolution. Such limitations are difficult to explain within the framework of the standard cosmological model. The third problem is the lack of monopoles. According to the standard model, at 1016 GeV the symmetry is violated, and monopoles should appear. If they could not be annihilated, then their ratio to the number of photons would have remained constant. Then, for one nucleon at the present time, there should be one monopole, which does not correspond to the experimental data.

The listed problems can be solved if we assume that in the early stages of evolution the universe expanded exponentially, as a result of which it became practically flat. However, the inflationary paradigm itself is beyond the scope of the standard model, and it has not been possible to justify it from the first principles to the present time. Another disadvantage is that it assumes the existence of structures that are many orders of magnitude larger than our universe. Such a prediction is difficult to verify experimentally.

In general, it can be noted that both the inflation model and alternative models (see, for example, [6,7]) contain a large number of adjustable parameters, which can be attributed to the shortcomings of both approaches.

On the other hand, there are still a number of important unresolved cosmological problems, among which we can mention the problem of the predominance of matter over antimatter. According to modern observations, antimatter is practically absent in our universe. Currently, a number of scenarios for this phenomenon have been proposed (see, for example, [8]), but its mechanism remains largely unclear. Note that most symmetry breaking scenarios also require going beyond the standard model.

The purpose of this article is to show that the listed problems can be solved by simply assuming that the universe in the early stages was not in a hot state but in a pure quantum state.

Expansion of the Universe: the Friedmann Equation or the Wave Function?

At present, it is believed that the universe originated from a hot, super-dense state. Further evolution of the universe is usually described on the basis of Friedmann equations, which are consequences of general relativity for the case of an isotropic fluid [8-10]. Such equations (containing thermodynamic parameters, such as, for example, pressure) can be applied to the case of local equilibrium in the universe. The presence of such an equilibrium is postulated.

An alternative is to simulate the expansion of the universe using the wave function. In the works by Hartle JB and Vilenkin A [11,12], the expansion of the universe was modeled on the basis of the Wheeler-de Witt equation, which has the form [13]:

Ĥ_WdW·Ψ=0

where Ĥ_WdW - is the Wheeler-de Witt Hamiltonian, and Ψ is the wave function of the universe. At the same time, a number of scenarios for the origin of the universe «from nothing» are proposed, when the total energy of the system (equal to the sum of the gravitational energy and particle energy) is zero. The Wheeler-de Witt equation is considered a good first approximation for describing the quantum evolution of the universe.

These two approaches are alternatives of each other, since in the first case, the thermodynamic equilibrium is postulated in the system (that is, the system is in a mixed state), and in the second case, there are no thermodynamic parameters in the system, and it itself is in a pure state.

In the second case of the pure state of the universe, the problem of self-action arises, since the universe acts «on itself» during the expansion. If the system is in local thermodynamic equilibrium, then such a problem does not arise, since some parts of the system can act on its other parts. However, for a pure state in the system, it is impossible to single out its «parts» - the system is described by a single wave function. Can a system, that is in the pure state, create a curvature of space, thereby determining its own dynamics?

The concept of a «Quantum Universe» often implies quantum gravity [14]. At the same time, it must be noted that a situation is possible where the particles behave in essentially a quantum way, and the fields do not. For example, in calculating energy levels in an atom, the quantization of fields can be largely ignored, based only on the quantum behavior of electrons (although the transition of the particle to a lower level itself is closely related to the quantization of fields). The quantization of gravity is assumed to be important at densities on the order of Planckian, but with further expansion of the universe, the effects of the quantization of gravity can be considered small. There is also a large number of approaches to the quantization of space-time [14], which will not be considered in this article.

The Model of the Pure Quantum State of the Universe

To solve the problems of flatness, homogeneity of the universe, and other problems listed above, we assume that the universe at the beginning of the expansion was in a pure quantum state. Such a statement with respect to the universe also requires some auxiliary (but natural) assumptions:

1. The universe was born «from nothing», that is, its total energy, including the gravitational energy and particle energy, was zero. That is, in the «initial» moment of time, the universe, in fact, was a free particle.

2. In the process of expansion, while the state of the universe is pure, the action of the universe on itself is absent. The curvature of space-time is strictly zero. That is, the universe expands in a flat space, representing a spherical wave

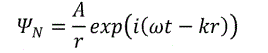
3. The pure state of the universe is metastable. As a result of interactions with vacuum fluctuations after a certain time τ_pure, the universe goes into a mixed state.

4. In the pure state, the universe is a condensate, described by a single wave function, in spite of the fact that it can consist of a large number of particles. Such a condensate can be treated as a set of entangled particles.

5. After the transition of the universe from a pure state to a mixed one as a result of many subsequent births and annihilation of particles, a local thermodynamic equilibrium is formed, i.e., universe is thermalized and heated (Figure 1).

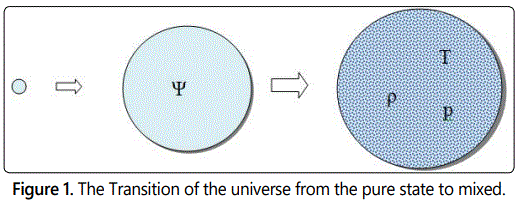
Since the universe is in a pure state, before decoherence (transition to a mixed state), one cannot speak about any definite curvature of space-time, since the equations of general relativity use only classical (non-quantum) parameters (compare, for example, one cannot speak of a definite position of a quantum particle before measurement). Consequently, the Friedmann equations at this stage of the expansion of the universe are not applicable.

Such an expansion process is largely similar to the EPR experiment, when a pair of particles has been initially in a singlet pure state and gradually move away from each other. In this case, such a pair of particles is described by a single wave function. As a result of measuring the parameters of one of the particles, the second particle also instantly passes into a mixed state.

We show that on the basis of the proposed model, the main problems of the initial stages of the expansion of the universe can be solved.

Entanglement, Superluminal Communication and the Horizon Problem

Let us first consider the basic properties of entangled particles and the laws of decay of entanglement. There are several definitions of the term «entanglement» see, for example, [15]. One definition is the following:

‘Entanglement implies that the whole system cannot be represented as a product of the subsystems’.

This property means that, prior to measurement, entangled particles behave as one particle whose behavior is described by a single wave function.

As will be shown below, the problem of homogeneity of temperatures of distant regions of the universe can be solved on the basis of superluminal communication. The problem of superlight communication has been considered repeatedly and has various aspects.

On the one hand, there are no-communication theorems. These theorems limit the speed of information transfer in an arbitrary quantum system (see, for example, [16]). Quantum entanglement can create the impression that information can be transmitted faster than the speed of light. However, according to the no- communication theorem, these phenomena do not allow true communication, they allow only two observers in different places to see the same system simultaneously, without any control over what they see.

On the other hand, in experiments with entangled particles [17], it was found that the signal about the measurement of the state of one particle from an entangled pair propagates at a speed much higher than the speed of light. One of the arguments against the propagation of information faster than the speed of light is also the possible violation of the second law of thermodynamics [18]. According to the author, if there is no interaction between two entangled particles (for example, in the EPR experiment), however, in the measurement of one particle the state of the second one also changes, this corresponds to an additional decrease in the entropy of the isolated system. Since such processes are forbidden by the second law of thermodynamics, this is what is considered by a number of authors as a prohibition of superluminal communication. However, this argument implicitly implies that there are thermodynamic parameters in the system, such as entropy, temperature, etc. However, for a system that is in a pure state, there are no grounds for introducing any thermodynamic parameters, since the system is not in equilibrium.

Another manifestation of superluminal communication is Wheelerʼs delayed experiments. Wheelerʼs thought experiment [19] is a variant of an experiment with two slits in which one of the slits can be closed after the photon has passed through both slits, but has not yet reached the screen. That is, in fact, the choice of the structure of the system with which the photon interacts is postponed. At present, this experiment is implemented, although in a slightly different form (see, for example, [20-25]).

Thus, we can draw the following conclusions on the problem of superluminal communication:

- Entangled particles can be connected with arbitrary speed (at least, as far as modern instruments allow it to be checked),

- With what speed information can be transferred from one point of the system to another - this is another matter. The answer to it largely depends on the definition of information. However, the information transfer rate has nothing to do with the speed of decoherence and thermalization. During decoherence, the information channel is not formed, since the transfer of the interaction occurs only in one direction.

Various scenarios of decoherence of qubits depending on their correlation length are considered in the study by Breuer HP et al. [26]. In particular, for the case when the correlation length is large, the collective interaction of qubits can lead to a significant enhancement of decoherence.

Thus, if the moving particles of the universe were entangled with each other, then these particles will simultaneously transit into their ground state (decay), no matter how far apart they are. This means that their further thermalization (associated with the creation and annihilation of other particles) will depend on the degree of entanglement of the initial state, but not on the size of the system.

Thus, at the initial pure stage of the evolution of the universe there are no thermodynamic parameters, and the size of the universe varies according to the law:

R=ct

Since the transition of some particles to the ground state depends significantly on the transition of others, this phenomenon can be treated as a phase transition.

Later, after establishing thermodynamic equilibrium, according to modern models (see, for example, [8]), the scale factor changed to the recombination epoch as

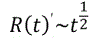
And after recombination epoch to present time as

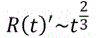
Thus, the problem of the horizon is resolved by the fact that entangled particles are thermalized, no matter what the distance between them, even if this distance exceeds the value of ct.

The Problem of the Flat Universe

Since in the pure phase (at times t<τ_pure) of the expansion of the universe it does not act on itself, then, as already noted above, the curvature of the universe remains zero throughout this entire phase. In classical mechanics, the self-interaction of particles is associated with the emission of electromagnetic waves by them (see, for example, [27]). The transition of the pure state of the system to the mixed one is caused just by the radiation of the particles. Therefore, until the particles (any) are radiated, and the system remains in a pure state, there is no self-action. Then in the process of expanding of universe during the pure phase, the following condition must be fulfilled:

Ω-1=0

where Ω=ρ/ρ_c characterizes the difference between the mean density ρ and the critical ρ_c one. This condition, which is a consequence of the purity of the quantum state, automatically solves the problem of fine tuning of the universe in the early stages. The problem of fine tuning is that extrapolating the known laws of the expansion of the universe within the standard cosmological model (without inflation) on Planck times tP requires a fine tuning of the parameter Ω, such that (see, for example, [28]):

0 ≤ Ω-1=10^-60

This would mean that the kinetic term at tP must have differed from the gravitational term by about one part in 1060. On the other hand, the kinetic and gravitational terms are now comparable.

Thus, at the beginning of the next stage, when the pure state is destroyed and thermodynamic equilibrium sets in, the average density of the universe is exactly equal to the critical one.

The Problem of Monopoles

Models of elementary particles assume that at energy greater than 1016 GeV the symmetry is violated. This leads to the inevitable emergence of monopoles [8]. If they could not annihilate, then their ratio to the number of photons will remain approximately constant. At that time, one monopole must now be present per nucleon, which is completely inconsistent with the experimental data.

Monopoles in fact were topological defects. The inflationary paradigm suggests that because of the exponential expansion of the universe, even if the monopoles existed at its early stages, after inflation their density turned out to be so small that it is not possible to detect them in our part of the universe. However, if the universe was in a pure state, then the absence of defects is quite natural. This absence can be considered one of the definitions of the pure state. Thus, in the process of expanding the universe in a pure quantum state, the monopoles could not exist. If after decoherence of the pure state temperature of the universe turned out to be insufficient (less than 1015 GeV), then the monopoles could not form at any significant level in this stage either.

The Problem of the Predominance of Matter over Antimatter

Since the matter currently predominates over antimatter, this fact needs to be justified. Since Sakharovʼs work [29], a number of mechanisms for baryogenesis have been proposed (see, for example, [30-32]), most of which go beyond the standard model and also require additional assumptions. The basic conditions for baryogenesis are as follows [8]:

1. There must be a physical process that violates the law of conservation of the baryon number.
2. There must be a violation of the invariance of C and CP.
3. There must be a violation of the state of thermal equilibrium.

Regarding these conditions, we can note that they are not directly related to the inflationary paradigm and require additional assumptions. Violation of C and CP-invariance was experimentally discovered, however how great is this effect? A weak violation of the conservation of baryon charge is predicted by several theories that go beyond the standard model (see also [33-36]). Can such a weak violation play a decisive role in nucleosynthesis? There is also a number of models of symmetry breaking and violation of thermal equilibrium [8].

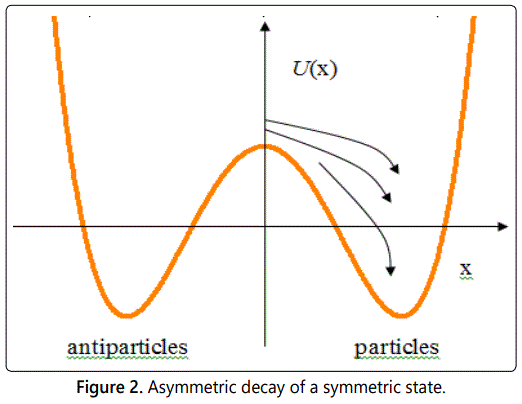
We show that this problem can also be solved on the basis of the entanglement of the expanding quantum system. Let us assume that the flying particles (condensate) with equal probability can decay into particles and antiparticles. In the absence of any asymmetry, the creation of a particle or antiparticle in this case is a random process (Figure 2). However, since particles (from which baryons are subsequently born) are entangled with one another, such a violation will occur immediately in the whole system, and not in its individual regions. That is, the resulting fluctuation will be significantly strengthened due to entanglement and will cover the entire system. Then the system will have either a matter or antimatter. If the entanglement between the original particles is not complete, then the predominance of matter over antimatter (or vice versa) will also be incomplete, but sufficient for the formation of baryons. As a result, after the annihilation of a part of the matter and antimatter, there will be an excess of one or the other.

After the collapse of the pure state of the universe, the temperature first increases strongly due to decoherence, and then the era of radiation domination occurs, during which the temperature begins to decrease. The further evolution of the universe can be described by known models, according to which, in the future (see, for example, [8]), the electroweak interaction separates from the strong one, then quarks and known elements are formed.

Another Consequences of the Model of Pure Universe

Since after decoherence, gravity «turns on» almost instantaneously, the acceleration also becomes essentially variable. Since gravitational waves are caused by variable acceleration, this should lead to the existence of primary gravitational waves. These waves must accompany the process of decoherence of the pure universe. The discovery of such waves is currently one of the important problems of experimental cosmology.

As already noted above, the decoherence of a large number of entangled particles can be treated as a phase transition. The most important property of such a phase transition is that it occurs simultaneously in the entire system and is not related to the presence of a critical nucleus. This property is characteristic of phase transitions of the second kind. In such systems, as well as in a wide class of systems associated with self-organized criticality, the perturbation spectrum is scale- invariant in view of the absence of a characteristic size in the system. As is known, this is the spectrum observed in the distribution of matter in galaxies (see, for example, [37]).

On the other hand, the power spectrum of perturbations may not be directly related to inflation or any other initial conditions. It is known that systems with dominant gravity (namely, the universe at a rather late stage) are not locally equilibrium, but represent essentially chaotic nonlinear systems with long-range interaction. In this case, the power spectrum is characteristic of a wide class of systems with gravity (see, for example, [38-40]), and weakly depends on the type of initial perturbations, and hence on the state of the universe in the early stages.

Conclusion

Thus, the pure state of the expanding universe in the early stages allows, without additional assumptions (within the framework of the standard model), to explain flatness and homogeneity of the universe from a single point of view, as well as the predominance of matter over antimatter and the absence of monopoles. Such a mechanism can be considered as an alternative to the inflationary paradigm.

References

1. Starobinskii AA. A New Type of isotropic cosmological models without singularity. Phys Lett B. 1980; 91(1): 99-102. doi: 10.1016/0370-2693(80)90670-X   
2. Guth AH. Inflationary universe: A possible solution to the horizon and flatness problems. Phys Rev D. 1981; 23(2): 347-356. doi: 10.1103/PhysRevD.23.347   
3. Albrecht A, Steinhardt PJ. Cosmology for grand unified theories with radiatively induces symmetry breaking. Phys Rev Lett. 1982; 48(17): 1220-1223. doi: 10.1103/PhysRevLett.48.1220   
4. Linde AD. A new inflationary universe scenario: a possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys Lett B. 1982; 108(6): 389-393. doi: 10.1016/0370-2693(82)91219-9   
5. Linde AD. Chaotic Ination. Phys Lett B. 1983; 129(3-4): 177-181. doi: 10.1016/0370-2693(83)90837-7   
6. Ijjas A, Steinhardt PJ, Loeb A. Inflationary paradigm in trouble after Planck. Phys Lett B. 2013; 723(4-5): 261-266. doi: 10.1016/j.physletb.2013.05.023   
7. Penrose R. Cycles of time: An extraordinary new view of the universe. 1^st edition. New York, NY: Knopf; 2011.   
8. Weinberg S. Cosmology. Oxford, OF: Oxford University Press; 2008.   
9. Friedmann A. About the curvature of the room. Magz Phys. 1922; 10(1): 377-386. doi: 10.1007/BF01332580   
10. Friedmann A. On the possibility of a world with a constant negative curvature of space. Magz Phys. 1924; 21(1): 326-332. doi: 10.1007/BF01328280   
11. Hartle JB, Hawking SW. Wave function of the universe. Phys Rev D. 1983; 28(12): 2960-2975. doi: 10.1103/PhysRevD.28.2960   
12. Vilenkin A. Birth of inflationary universes. Phys Rev D. 1983; 27: 2848-2855. doi: 10.1103/PhysRevD.27.2848   
13. DeWitt BS. Quantum Theory of Gravity. I. The Canonical Theory. Phys Rev. 1967; 160(5): 1113-1148. doi: 10.1103/PhysRev.160.1113   
14. Bojowald M. Quantum cosmology: a review. Rep Prog Phys. 2015; 78(2): 023901. doi: 10.1088/0034-4885/78/2/023901   
15. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys. 2009; 81: 865-942. doi: 10.1103/RevModPhys.81.865   
16. Peres A, Terno DR. Quantum information and relativity theory. Rev Mod Phys. 2004; 76(1): 93-123. doi: 10.1103/RevModPhys.76.93   
17. Salart D, Baas A, Branciard C, Gisin N, Zbinden H. Testing the speed of ‘spooky action at a distance’. Nature. 2008; 454: 861-864. doi: 10.1038/nature07121   
18. Peacock KA, Hapburn PS. Begging the signaling question: quantum signaling and the dynamics of multiparticle systems. Quantum Physics. 1999.   
19. Wheeler JA. The “past” and the “delayed-choice” double-slit experiment. Mathematical Foundations of Quantum Theory. 1978; 9-48. doi: 10.1016/B978-0-12-473250-6.50006-6   
20. Kim YH, Yu R, Kulik SP, Shih YH, Scully M. Delayed “choice” Quantum Eraser. Phys Rev Lett. 2000; 84: 1-5. doi: 10.1103/PhysRevLett.84.1   
21. Walborn SP, Terra Cunha MO, Pádua S, Monken CH. Double-slit quantum eraser. Phys Rev A. 2002; 65(3): 033818. doi: 10.1103/PhysRevA.65.033818   
22. Jacques V, Wu E, Grosshans F, et al. Experimental realization of Wheelerʼs delayed-choice gedanken experiment. Science. 2007; 315: 966-968. doi: 10.1126/science.1136303   
23. Kaiser F, Courdeau T, Milman P, Ostrowsky DB, Tanzilli S. Entanglementenabled delayed-choice experiment. Science. 2012; 338(6): 637-640. doi: 10.1126/science.1226755   
24. Peruzzo A, Shadbolt P, Brunner N, Popescu S, OʼBrien JL. A quantum delayed-choice experiment. Science. 2012; 338(6107): 634-637. doi: 10.1126/science.1226719   
25. Ma XS, Zotter S, Kofler J, et al. Experimental delayed-choice entanglement swapping. Nature Physics. 2012; 8: 479-484. doi: 10.1038/nphys2294   
26. Breuer HP, Petruccione F. The theory of open quantum systems. Oxford, OF: Oxford University Press; 2002.   
27. Landau LD, Lifshitz EM. The Classical Theory of Fields. 4^th edition. Oxford, OF: Pergamon Press; 1975.   
28. Coles P, Lucchin F. Cosmology. Chichester, CH: Wiley; 1997.   
29. Sakharov AD. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. JETP Lett. 1967; 5: 24-27.   
30. Kuzmin VA, Rubakov VA, Shaposhnikov ME. On anomalous electroweak baryon-number non-conservation in the early universe. Phys Lett B. 1985; 155(1-2): 36-42. doi: 10.1016/0370-2693(85)91028-7   
31. Dolgov A, Silk J. Baryon isocurvature fluctuations at small scales and baryonic dark matter. Phys Rev D. 1993; 47: 4244-4255. doi: 10.1103/PhysRevD.47.4244   
32. Kusenko A, Pearce L, Yang L. Postinflationary Higgs relaxation and the origin of matter-antimatter asymmetry. Phys Rev Lett. 2015; 114: 061302. doi: 10.1103/PhysRevLett.114.061302   
33. Trodden M. Electroweak baryogenesis. Rev Mod Phys. 1999; 71(5): 1463-1500. doi: 10.1103/RevModPhys.71.1463   
34. Asaka T, Shaposhnikov M. νMSM, dark matter and baryon asymmetry of the universe. Phys Lett B. 2005; 620(1-2): 17-26. doi: 10.1016/j.physletb.2005.06.020   
35. Davidson S, Nardi E, Nir Y. Leptogenesis. Phys Rep. 2008; 466(4-5): 105-177. doi: 10.1016/j.physrep.2008.06.002   
36. Giovannini M. Hypermagnetic gyrotropy, inflation, and the baryon asymmetry of the Universe. Phys Rev D. 2015; 92(12): 121301. doi: 10.1103/PhysRevD.92.121301   
37. Harrison ER. Fluctuations at the threshold of classical cosmology. Phys Rev D. 1970; 1(10): 2726-2730. doi: 10.1103/PhysRevD.1.2726   
38. Aschwanden MJ, Crosby NB, Dimitropoulou M, et al. 25 years of selforganized criticality: solar and astrophysics. Space Sci Rev. 2016; 198(1-4): 47-166. doi: 10.1007/s11214-014-0054-6   
39. Melkikh EA, Melkikh AV, Tokmantsev VI. Non-equilibrium fluctuations in the ring of material points with gravity. Mod Phys Lett B. 2017; 31(1): 1650425. doi: 10.1142/S021798491650425X   
40. Tamayo D, Markham SR, Hedman MM, Burns JA, Hamilton DP. Radial profiles of the Phoebe ring: A vast debris disk around Saturn. Icarus. 2016; 275: 117-131. doi: 10.1016/j.icarus.2016.04.009