Abstract

The nonlinear propagation of dust-ion-acoustic (DIA) waves in an unmagnetized collisionless degenerate dense plasma (containing degenerate electron, positron, ion fluids and negatively charged dust grains) have been theoretically investigated. The Burgersʼ equation has been derived by employing the reductive perturbation method and by taking the effect of viscous force in the ion fluid into account. The stationary shock wave solution of Burgersʼ equation is obtained, and numerically analyzed in order to identify the basic properties of dust-ion-acoustic shock structures. It has been shown that depending on plasma parametric values, the degenerate plasma under consideration supports compressive or rarefactive shock structures. The relevance of our results in astrophysical objects like white dwarfs and neutron stars, which are of scientific interest, are briefly discussed.

PACS numbers: 52.27.Ny, 52.35.Fp, 52.35.Tc, 52.25.Vy

Keywords: Dust-ion-acoustic waves; Shock waves; Degenerate pressure; Relativistic factor; Compact objects.

Introduction

Now-a-days, the linear properties of the DIA waves in dusty plasmas are well understood from both theoretical and experimental points of view [1-5]. Recently, the nonlinear waves particularly the DIA shock waves (DIA ShWs) have received an impressive interest in realizing the basic properties of localized electrostatic perturbations in space and laboratory dusty plasmas. The physics of quantum plasmas, rapidly grown beyond conventional plasmas found in space or laboratory for many years [6,7]. This is mainly due to the potential applications of quantum plasmas in different areas of scientific and technological importance [8-11]. It is a common idea that electron-positron plasmas have presumably appeared in the early universe [12,13] and are frequently encountered in active galactic nuclei [14] and in pulsar magnetospheres [15,16]. This electron-positron-ion plasma is usually characterized as a fully ionized gas consisting of electrons and positrons of equal masses. Recently, there has been a great deal of interest in studying linear as well as nonlinear wave motions in such plasmas [17,19]. However, most of the astrophysical plasmas usually contains ions, in addition to the electrons and positrons. Clearly, the properties of wave motions in an electron-positron-ion plasma should be different from those in two-component electron-positron plasmas. For example, Rizzato [20] and Berezhiani et al. [21] have investigated envelope solutions of electromagnetic waves in three-component electron-positron-ion plasmas.

The electron-positron-ion plasmas are thought to be generated naturally by pair production in high energy processes in the vicinity of several astrophysical objects as well as produced in laboratory plasmas experiments with a finite life time [22]. Because of the long life time of the positrons, most of the astrophysical [23] and laboratory plasmas [24] become a mixture of positrons, which is the analog of recombination in plasma composed of ions and electrons, is relatively unimportant in classical [25], as well as in dense plasmas [26] to study the collective plasma oscillations. The ultra dense degenerate electron-positron plasmas with ions are believed to be found in compact astrophysical bodies like neutron stars and the inner layers of white dwarfs [26-29] as well as in intense laser-matter interaction experiments [30,31].

Now-a-days, a number of authors have become interested to study the properties of matter under extreme conditions [32-36]. Recently, a number of theoretical investigations have also been made of the nonlinear propagation of electrostatic waves in degenerate quantum plasma by a number of authors [37-39] etc. However, these investigations are based on the electron equation of state valid for the non-relativistic limit. Some investigations have been made of the nonlinear propagation of electrostatic waves in degenerate dense plasma based on the degenerate electron equation of state valid for ultra relativistic limit [40-42]. We are interested to study the dissipation relation of the DIA ShWs in a degenerate e-p-i plasma system where we have added positrons for the rather long lifetime of positrons, most of the astrophysical [14,16-18,23,29,43-45] as we have mentioned in the introductory chapter. The DIA ShWs are longitudinal oscillations of the ions (and the electron-positron) a dusty e-p-i plasma. The linear dispersion relation (DR) will give the relation between the wave frequency 'ω and the wave number 'κ. The number density of the degenerate electron and positron in a compact object is so high (e. g. in white dwarfs, the degenerate electron number density can be order of 10³⁶ cm^-3 even more, and order of 10³⁶ cm^-3 even more in neutron stars) that the non-relativistic limit is not practically applicable for de-generate fermions (electron-positron-ions). The equation of state for degenerate particles in astrophysical compact objects is the ultra-relativistic limit mathematically explained by S. Chandrasekhar [33]. It is very important to note that the degenerate pressure depends only on the fermion number density, but not on its temperature.

To the best of our knowledge, no theoretical investigation has been developed to study the extreme condition of matter for both non-relativistic and ultra-relativistic limits in a degenerate plasma system with the nonlinear propagation and formation of the dust-ion-acoustic shock waves (DIA ShWs). Therefore, in our present investigation, we consider a degenerate dense plasma system in absence of the magnetic field containing nonrelativistic degenerate cold ion fluid, both non-relativistic and ultra-relativistic degenerate electrons and positrons where the ion is the heavier element among all other elements. To study the basic features of the dust-ion-acoustic nonlinear structures of shock wave in such unmagnetized three component degenerate dense plasma, we have studied the Burgersʼ equation and the numerical solution of Burgersʼ equation. The model is relevant to compact interstellar objects (e. g., white dwarf, neutron star, etc.) [46].

Governing equations

We consider an unmagnetized collisionless degenerate dense plasma system consisting of non-relativistic degenerate cold degenerate ion fluid and both non-relativistic and ultra-relativistic degenerate electrons and positrons fluids and negatively charged dust grains. The dynamics of the one dimensional DIA ShWs in such a degenerate dense plasma system is governed by

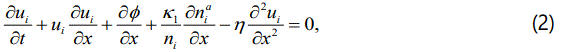
where μ is the ratio of the number density of negatively charged dust and ion (Z_dn_d0/n_io) & μ=1+α_p-α_e,n_s is the plasma number density of the species s (s = e for electron, i for ion, and p for positron) normalized by its equilibrium value n_so(n_eo), u_s, is the plasma species fluid speed normalized by C_im=(m_ec²/m_i)^1/2 with m_e(m_i) being the electron (ion) rest mass mass and c being the speed of light in vacuum, Φ is the electrostatic wave potential normalized by m_ec²/e with e being the magnitude of the charge of an electron, the time variable (t) is normalized by ω_pi=(4πn₀e²/m_i)^1/2 and the space variable (x) is normalized by λ_m=(m_ec²/4πn₀e²)^1/2. The coefficient of viscosity η is a normalized quantity given by ω_iλ²_mim_sn_so, and α_e is the ratio of the number density of electron and ion (n_e/n_i) and α_p is the ratio of the number density of positron and ion (n_p/n_i). The constants K₁=n₀^α-1K_i/m_i²C_i² and K₂=n₀^γ-1K_e/m_iC_i²=n₀^γ-1K_p/m_iC_i². The equations of state used here for the degenerate pressures of electrons, ions and positrons are given by

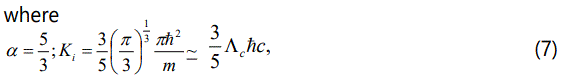
for the non-relativistic limit (where Λ_c = πћ²/mc = 1.2 × 10^-10 cm, and ћ is the Planck constant divided by 2π).

While for the electron fluid,

and while for the positron fluid

where for non-relativistic limit [33-35,40,42]

and for the ultra-relativistic limit [33-35,40,42]

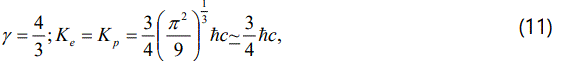
Derivation of Burgersʼ equation

Now we derive a dynamical equation for the nonlinear propagation of the dust-ion-acoustic shock waves by using (1 - 5). To do so, we employ a reductive perturbation technique to examine electrostatic perturbations propagating in the relativistic degenerate dense dusty plasma due to the effect of dissipation, we first introduce the stretched coordinates [47]

where V_p is the wave phase speed (ω /κ with ω being angular frequency and κ being the wave number of the perturbation mode), and ∈ is a smallness parameter measuring the weakness of the dispersion (0 < ∈ < 1). We then expand n_i, n_e, u_i, and Φ, in power series of ∈:

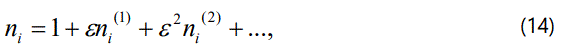
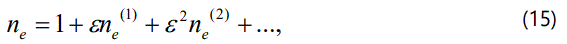
and develop equations in various powers of ∈. To the lowest order in ∈, using equations (12)-(18) into equations (1)-(5) we get as, 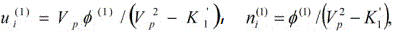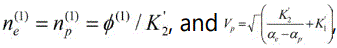and 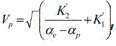, where 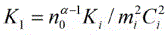and 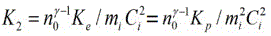. The relation represents 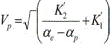the dispersion relation for the ion-acoustic type electrostatic waves in the degenerate plasma under consideration. We are interested in studying the nonlinear propagation of these dissipative dust-ion-acoustic type electrostatic waves in a three components degenerate plasma. To the next higher order in ∈, we obtain a set of equations

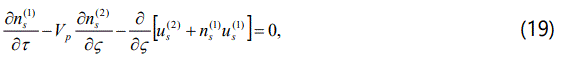
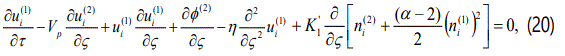
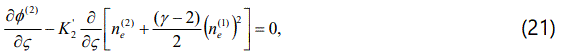
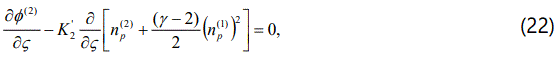
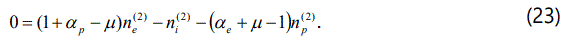
Now, combining (19-23) we deduce a Burgers² equation

where the value of A and C are given by

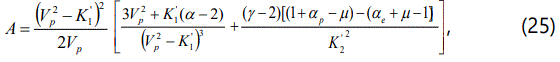
The shock wave solution of (24) is

where the special stretched coordinates, ξ = ζ - u₀τ, the amplitude, Φ_m = u₀/A the width, δ = 2C/u₀, u₀ is the wave speed and the parameter η was chosen from standard value [48] for the system under consideration.

Numercial analysis

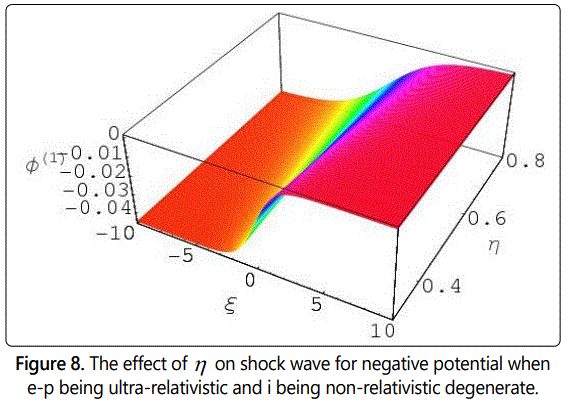
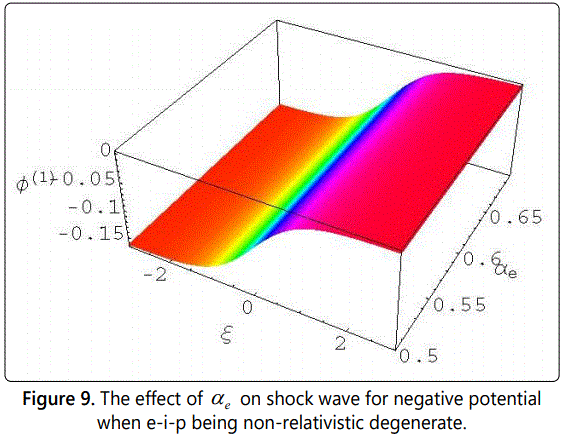
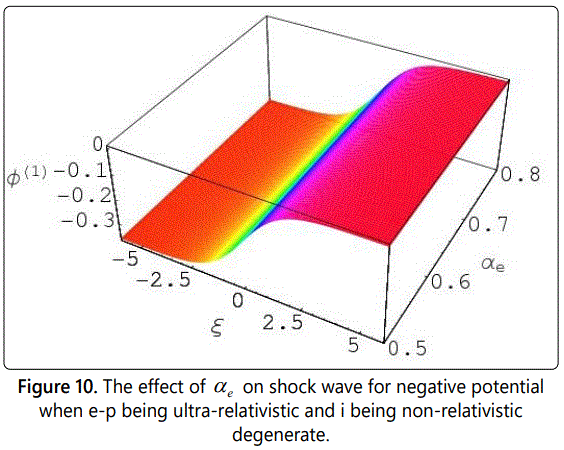
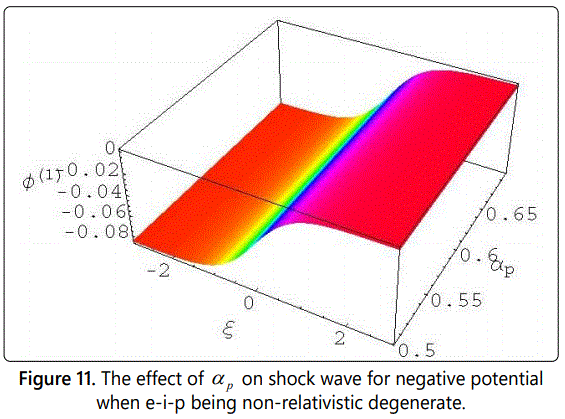
We have numerically solved the Burgersʼ equation(24), and have studied the effects of η, α_e, and α_p with ξ on dust-ion-acoustic nonlinear structures of shock waves in both non-relativistic and ultra-relativistic degenerate electrons and positrons where ions always being non-relativistic degenerate. It is obvious from figures 1-12 that the degenerate plasma system under consideration supports compressive and reductive DIA ShWs which are associated with both positive and negative potential and the amplitude of these nonlinear structures of shock waves depends on the Chandrasekhar limits [33], i.e. non-relativistic and ultra-relativistic limits.

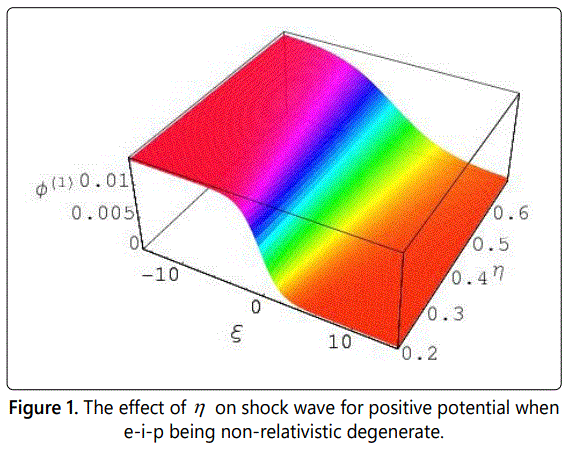
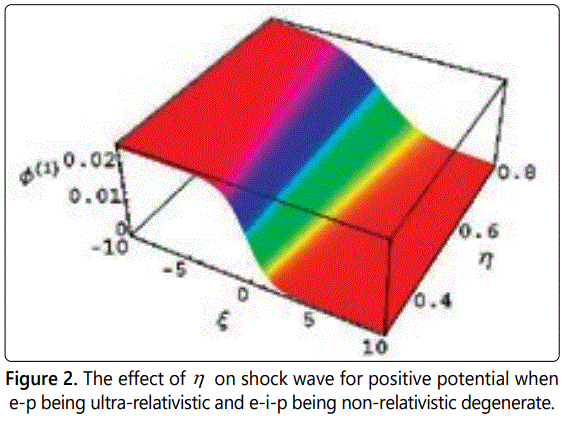
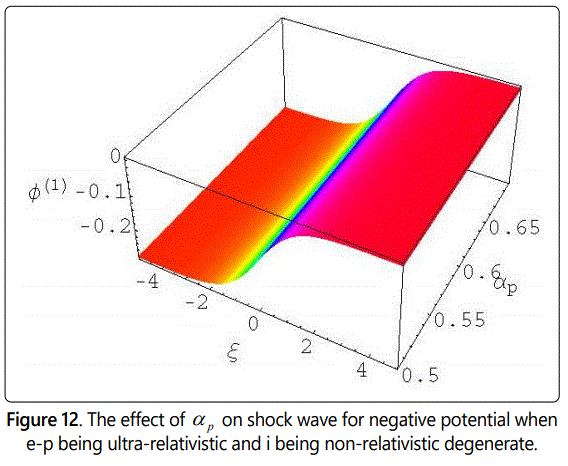
In figures 1-6 we have observed the effect of η, α_e, α_p, and μ on the potential structure with the variation of ξ in case of both non-relativistic and ultra relativistic limits. It has been observed when the values of μ is smaller than 0.82 (μ < 0.82) then we observe the formation of positive potential for the nonlinear structures of compressive shock wave in our considered degenerate plasma system. Again we consider the values of μ is greater than or equal to 0.82 (μ > 0.82) then we observe the negative potential for the nonlinear refractive structures as shown in figures from 7 to 12. It should be noted here that in both cases we keep all the parameters same so that it could be easy to analysis the effects of every parameter. The interesting point is that with the increasing values of α_p and α_e, the values of potential increases smoothly, but the increasing values of η the potential decreases smoothly. It should be noted that the formation of the compressive dust-ion-acoustic shock waves depends only on the values of the ratio of the electron number density and the ion number density (α_e) and does not depend on the values of α_p (the ratio of the electron number density and the positron number density). And the figures 1-12 also show us that the potential for electron-positron (e-p) being ultra-relativistic and ion (i) being non-relativistic degenerate is always greater than for electron-ion-positron (e-i-p) being non-relativistic degenerate.

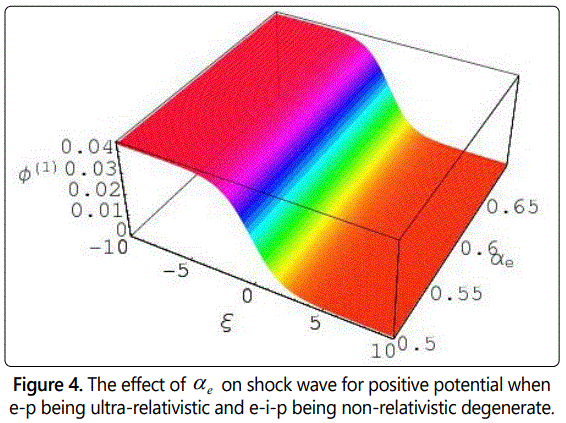
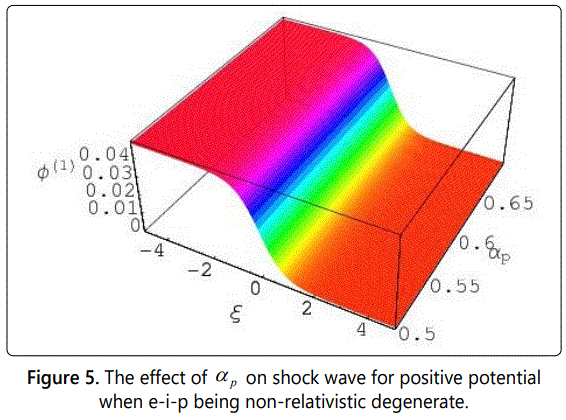
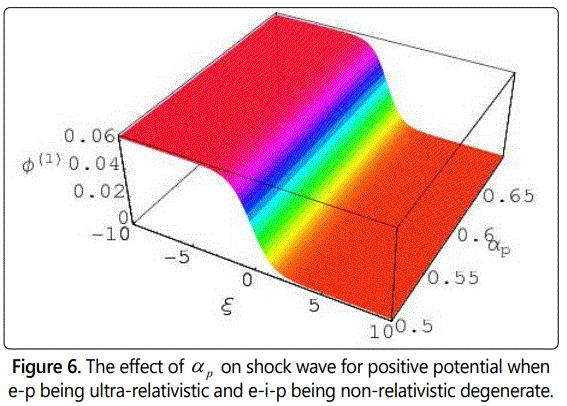
From the study of the negative potential in our three components degenerate plasma system, we have observed that with the increasing value of η the potential also increases. But it has been also noted that with the increasing values of η the potential, (Φ⁽¹⁾) also decreases very smoothly in both limits from figures 7 to 12. It should be noted here that in this case, the values of μ is always greater than or equal to 0.82 (μ > 0.82). It needs to be pointed here that the formation of the reductive DIA ShWs (shown in figures 7 to 12) depends only on the values of the ratio of the dust number density and the ion number density (μ) and does not depend on the values of α_e and α_p (the ratio of the number density of electron and ion and the ratio of the positron number density and ion). From the analysis of the negative potential structures for μ ≥ 0.82 (shown in figures 7 -12) it has been again pointed out that the potential for electron-positron (e-p) being ultra-relativistic and ion (i) being non-relativistic degenerate is always greater than for electron-ion-positron (e-i-p) being non-relativistic degenerate.

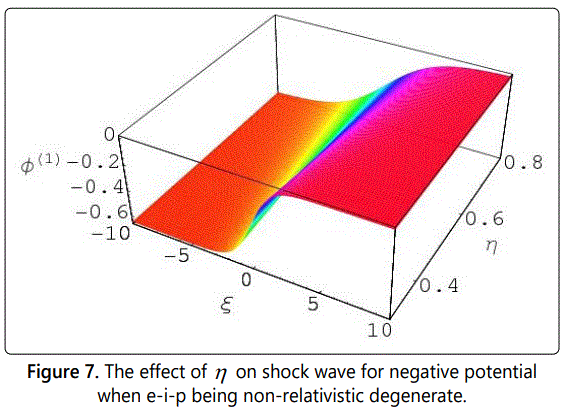
The profiles of shock wave, caused by the balance between nonlinearity and dissipation, are depicted in figures 1-12. And the potential of the dust-ion-acoustic shock waves profiles for non-relativistic degenerate ions fluid and ultra-relativistic degenerate electrons and positron fluid is different from that when all the particles follow the same limit. From the mathematical calculation and the numerical solution of Burgersʼ equation we have found that for a certain value of μ we get both positive and negative potential when all other parameters are kept same, i.e. when the values of μ is always less than 0.82 (μ < 0.82) then we obtain positive potential and when the values of μ is greater than or equal to 0.82 (μ ≥ 0.82) then we obtain negative potential. It has made the great interest in the study of the dust-ion-acoustic nonlinear structures of shock waves in an unmagnetized degenerate dense plasma system to analysis the existence conditions for the positive and negative potential where the elements electrons, ions, and positrons are always being degenerate.

It is to be noted here that we have taken all the parameters in normalized form, so all the ranges of parameters are taken arbitrarily.

Discussion

We have considered an unmagnetized degenerate dense plasma containing non-relativistic degenerate cold ions fluid, both non-relativistic and ultra-relativistic degenerate electrons and positrons fluid, and negatively charged dust grains. We have examined the basic features of the electrostatic nonlinear structures that are found to exist in such degenerate dense plasma. In our present investigation all the degenerate constitutes of the considered dense unmagnetized plasma system follow relativistic limits of pressure. The nonlinear DIA shock waves and its propagation have been described thoroughly with Burgersʼʼ equation (24) and itʼs solution (27). The effects of different plasma parameters on the nonlinear propagation of DIA shocks waves have been graphically shown (Figures 1-12).

Our present investigation is different from the related Investigations [40-43,49,50] in the way that we have considered the pressure of all the constituent particle (electrons and ions), as the whole system is degenerate and all the particles should follow the equation of state [6-11] whatever the limit is (non relativistic or ultra-relativistic). This is obvious that the shock profiles obtained from our present investigation are also quite different from the previous investigation [40-42,49,51] in the sense that we have had electrostatic shock profiles while the others have got to support electrostatic solitary profiles [40-42] and double layers [40,41]. The degenerate dense plasma is found to support shock structures whose basic features dependent on the plasma number density. From this point of view our present investigation is more acceptable and the system constituents havemade the validity of our investigations unique.

We note that in our numerical analysis we have used a wide range of the degenerate plasma parameters [33,40,42,49,52,53], which are relevant for many cosmic environments and compact astrophysical objects. The results of the present investigation is, therefore, expected to be useful in understanding the dispersion properties of the electrostatic shock waves in such cosmic environments [14,16,23], compact astrophysical objects [17,18,29] and interstellar compact objects [44,45]. The electrostatic waves in an ultra-relativistic and non-relativistic degenerate dense plasma, which is relevant to interstellar compact objects like white dwarfs, have been investigated. The results, which have been found from this investigation, represent ion acoustic-type of electrostatic waves in which the restoring force comes from the electron-ion degenerate pressure and inertia is provided by the ion mass density.

It can be expected that the basic features and the underlying physics of the DIA shock waves with the existence conditions for positive and negative potential, that have been presented in our present work should be verified by further laboratory experiments. It may also be added here that our investigation is valid for small amplitude DIA shock waves and for unmagnetized and uniform degenerate dense plasma system. These results may be useful to explain some aspects of shock waves in dense e-p-i degenerate plasma. However, arbitrary amplitude DIA shock waves in uniform/nonuniform degenerate dense plasma with or without the external magnetic field are also problems of recent interest for many space and laboratory dusty plasma situations, but beyond the scope of our present investigation. Although such plasma cannot be produced in a laboratory, yet they are gaining considerable attention of the researchers working on degenerate dense astrophysical plasma and numerical simulations. We hope that our present investigation will be helpful for understanding the basic features of the localized electrostatic disturbances in compact astrophysical objects (e.g. white dwarfs, neutron stars, black hole, etc.).

Acknowledgments

P. Halder is profoundly grateful to the Ministry of Science and technology (Bangladesh) for awarding the National Science and Technology (NST) fellowship.

References

1. Shukla PK, Mamtm AA. Introduction to Dusty Plasma Physics. 1st edition. Bristol, BS: Institute of Physics Publishing Ltd; 2002.   
2. Shukla PK, Silin VP. Dust ion-acoustic wave. Phys Scr. 1992; 45(5): 508. doi: 10.1088/0031-8949/45/5/015   
3. Barkan A, DʼAngelo N, Merlino RL. Experiments on ion-acoustic waves in dusty plasmas. Planet Space Sci. 1996; 44(3): 239-245. doi: 10.1016/0032-0633(95)00109-3   
4. Merlino RL, Barkan A, Thompson C, DʼAngelo N. Laboratory studies of waves and instabilities in dusty plasmas. Phys Plasmas. 1998; 5: 1607. doi: 10.1063/1.872828   
5. Shukla PK, Rosenberg M. Boundary effects on dust-ion-acoustic and dust-acoustic waves in collisional dusty plasmas. Phys Plasmas. 1999; 6(3): 1038. doi: 10.1063/1.873345   
6. Manfredi G. How to model quantum plasmas. Fields Institute Communications. 2005; 46: 263-287.   
7. Bonitz M, Filinov A, Böning J, Dufty JW. Introduction to Quantum Plasmas. In: Bonitz M, Horing N, Ludwig P (eds). Introduction to Complex Plasmas. Springer; 2010.   
8. Markowich PA, Ringhofer CA, Schmeiser C. Semiconductor Equations. 1st edition. Vienna, VE: Springer; 1990.   
9. Agrawal G. Nonlinear Fiber Optics. 2nd edition. San Diego, SD: Academic Press; 1995.   
10. Tanner PJ, Gallagher TF. Dipole-Dipole Excitation and Ionization in an Ultracold Gas of Rydberg Atoms. Phys Rev Lett. 2005; 94(17): 173001. doi: 10.1103/PhysRevLett.94.173001   
11. Kremp D, Bornath T, Bonitz M, Schlanges M. Quantum kinetic theory of plasmas in strong laser fields. Phys Rev E. 1999; 60: 4725. doi: 10.1103/PhysRevE.60.4725   
12. Misner W, Thorne KS, Wheeler JA. Gravitation. 1^st edition. San Francisco, SF: W. H. Freeman and Company; 1973.   
13. Gibbons GW, Hawking SW, Siklos STC. The Very Early Universe. Cambridge, CB: Cambridge University Press; 1983.   
14. Miller HR, Witta PJ. Active Galactic Nuclei. Berlin, BE: Springer-Verlag; 1988.   
15. Goldreich P, Julian WH. Pulsar Electrodynamics. Astrophys J. 1969; 157: 869-880. doi: 10.1086/150119   
16. Michel FC. Theory of pulsar magnetospheres. Rev Mod Phys. 1982; 54(1): 1-66. doi: 10.1103/RevModPhys.54.1   
17. Shukla PK, Rao NN, Yu MY, Tsintsadze NL. Relativistic nonlinear effects in plasmas. Phys Rep. 138(1-2): 1-149. doi: 10.1016/0370-1573(86)90157-2   
18. Yu MY, Shukla PK, Stenflo L. Alfven vortices in a strongly magnetized electron-position plasma. Astrophys J. 1986; 309: L63-L66.   
19. Michel FC. Theory of Neutron Star Magneto-spheres. 1^st edition. Chicago, CH: Chicago University Press; 1991.   
20. Rizzato FB. Weak nonlinear electromagnetic waves and lowfrequency magnetic-field generation in electron-positron-ion plasmas. Plasma Phys. 1988; 40(2): 289-298. doi: 10.1017/S0022377800013283   
21. Berezhiani VI, El-Ashry MY, Mofiz UA. Theory of strongelectromagnetic-wave propagation in an electron-positron-ion plasma. Phys Rev E. 1994; 50: 448. doi: 10.1103/physreve.50.448   
22. Mishra MK Tiwari RS, Jain SK. Small amplitude ion-acoustic double layers in multicomponent plasma with positrons. Phys Rev E. 2007; 76: 036401. doi: 10.1103/PhysRevE.76.036401   
23. Tandberg-Hanssen E, Emslie AG. The Physics of Solar Flares. Cambridge, CB: Cambridge University Press; 1988.   
24. Greaves RG, Surko CM. An Electron-Positron Beam-Plasma Experiment. Phys Rev Lett. 1995; 75: 3846. doi: 10.1103/PhysRevLett.75.3846   
25. Surko CM, Murphy TJ. Use of the positron as a plasma particle. Phys Fluids B. 1990; 2(6): 1372. doi: 10.1063/1.859558   
26. Alia S, Moslemb WM, Shuklac PK, Schlickeiser R. Linear and nonlinear ion-acoustic waves in an unmagnetized electron-positron-ion quantum plasma. Phys Plasmas. 2007; 14(8): 082307. doi: 10.1063/1.2750649   
27. Lai D. Matter in strong magnetic fields. Rev Mod Phys. 2011; 73(3): 629. doi: 10.1103/RevModPhys.73.629   
28. Harding AK, Lai D. Physics of strongly magnetized neutron stars. Rep Prog Phys. 2006; 69(9): 2631. doi: 10.1088/0034-4885/69/9/R03/pdf   
29. Shapiro SL, Teukolsky SA. Black holes, White dwarfs and neutron Stars: The Physics of Compact objects. 1^st edition. New York, NY: John Wiley and Sons; 1983.   
30. Berezhiani VI, Tskhakaya DD, Shukla PK. Pair production in a strong wake field driven by an intense short laser pulse. Phys Rev A. 1992; 46: 6608. doi: 10.1103/PhysRevA.46.6608   
31. Lebo IG, Tishkin VF. Hydrodynamic last abilities in ICF Problems. 2006.   
32. Halder P, Mamun AA. Influence of Compressive and Rarefactive IonAcoustic Shock Waves in a Multi-Component Degenerate Dense Plasma. IOSR Journal of Applied Physics. 2016; 8(4): 100-107. doi: 10.9790/4861-080402100107   
33. Chandrasekhar S. Exact solutions to the equation describing cylindrical solitons. Mon Not R Astron Soc. 1935; 170: 405.   
34. Chandrasekhar S. XLVIII. The density of white dwarf stars. Phil Mag. 1931; 11: 592.   
35. Chandrasekhar S. The Maximum Mass of Ideal White Dwarfs. Astrophys J. 1931; 74: 81. doi: 10.1086/143324   
36. Chandrasekhar S. Stellar Configurations with Degenerate Cores. The Observatory. 1934; 57: 373-377.   
37. Hass F. Variational approach for the quantum Zakharov system. Phys Plasmas. 2007; 13: 042309. doi: 10.1063/1.2722271   
38. Misra AP, Samanta S. Quantum electron-acoustic double layers in a magnetoplasma. Phys Plasmas. 2008; 15: 122307. doi: 10.1063/1.3040014   
39. Misra AP, Banerjee S, Haas F, Shukla PK, Assis LPG. Temporal dynamics in the one-dimensional quantum Zakharov equations for plasmas. Phys Plasmas. 2010; 17(3): 032307. doi: 10.1063/1.3356059   
40. Mamun AA, Shukla, PK. Solitary waves in an ultrarelativistic degenerate dense plasma. Phys Plasmas. 2010; 17(10): 104504. doi: 10.1063/1.3491433   
41. Roy N, Tasnim S, Mamun AA. Solitary waves and double layers in an ultra-relativistic degenerate dusty electron-positron-ion plasma. Phys Plasmas. 2012; 19(3): 033705. doi: 10.1063/1.3688877   
42. Mamun AA, Shukla PK. Arbitrary amplitude solitary waves and double layers in an ultra-relativistic degenerate dense dusty plasma. Phys Lett A. 2010; 374(41): 4238-4241. doi: 10.1016/j.physleta.2010.08.038   
43. Mamun AA, Halder P, Mukta KN. Nonplanar shock waves in a four component relativistic degenerate dense plasma. International Journal Research Develop Organisation. 2015; 2(4): 7.   
44. Silva LO, Bingham R, Dawson JM, Mendonça JT, Shukla PK. Neutrino Driven Streaming Instabilities in a Dense Plasma. Phys Rev Lett. 1999; 83(14): 2703. doi: 10.1103/PhysRevLett.83.2703   
45. Hoyos J, Reisenegger A, Valdivia JA. Magnetic field evolution in neutron stars: one-dimensional multi-fluid model. Astron Astrophys. 2008; 287: 789-803. doi: 10.1051/0004-6361:200809466   
46. Koester D, Chanmugam G. Review: Physics of white dwarf stars. Rep Prog Phys. 1990; 53(7): 837-915. doi: 10.1088/0034-4885/53/7/001   
47. Maxon S, Viecelli J. Spherical Solitons. Phys Rev Lett. 1974; 32(1): 4. doi: 10.1103/PhysRevLett.32.4   
48. Pick RM, Hildalgo C, Van Milligen BP, Helfenstein P. 32nd EPS Conference on Plasma Physics. Tarrogona, Spain. 2005.   
49. Moghanjoughi MA. Effects of ion-temperature on propagation of the large-amplitude ion-acoustic solitons in degenerate electronpositron-ion plasmas. Phys Plasma. 2010; 17(8): 082315. doi: 10.1063/1.3480117   
50. Khan SA, Mirza AM. Shocks and Solitons in Ultradense Degenerate Electron-Positron-Ion Plasmas. Commun Theor Phys. 2011; 55: 151. doi: 10.1088/0253-6102/55/1/27   
51. Lontano M, Bulanov SV, Koga J, Passoni M, Tajima T. A kinetic model for the one-dimensional electromagnetic solitons in an isothermal plasma. Phys Plasmas. 2002; 9(6): 2562. doi: 10.1063/1.1476307   
52. Huang C, Lu Q, Wang S. The mechanisms of electron acceleration in antiparallel and guide field magnetic reconnection. Phys Plasma. 2010; 17(7): 072306. doi: 10.1063/1.3457930   
53. Halder P, Mukta KN, Mamun AA. Properties of electron-ion acoustic solitary waves in a four component degenerate quantum plasma. International Journal of Current Research. 2018; 6: 70044-70058.