Research Article
Five-Dimensional anisotropic Dark energy Cosmological model in the presence of Scalar-Meson fields in General relativity
1Department of Applied Mathematics, Andhra University, Visakhapatnam, India
2Mathematics Department, IIIT, Srikakulam, RGUKT-AP, India
*Corresponding author: DRK Reddy, Department of Applied Mathematics, Andhra University, Visakhapatnam, India, Tel: +91 9441878067, E-mail: reddy_einstein@yahoo.com
Received: February 14, 2019 Accepted: March 13, 2019 Published: March 19, 2019
Citation: Reddy DRK, Ramesh G. Five-dimensional anisotropic Dark energy Cosmological model in the presence of Scalar-meson fields in General relativity. Int J Cosmol Astron Astrophys. 2019; 1(2): 67-70. doi: 10.18689/ijcaa-1000116
Copyright: © 2019 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Our interest, in this paper, is to present a new dark energy model in a five-dimensional Kaluza-Klein anisotropic space-time in the presence of scalar-meson fields in general relativity. To solve Einstein field equations we use (i) a relation between the metric potentials and (ii) a hybrid expansion law for the average scale factor proposed by Akarsu et al. [1]. The model obtained shows a transition of the universe from decelerated phase to accelerated phase of the universe which is in accordance with the present scenario of modern cosmology. Also we have constructed the dynamical parameters, namely, EoS parameter, the energy density, deceleration parameter, jerk parameter. The physical significance of these parameters with reference to the model obtained is discussed.
Keywords: Kaluza-Klein model; Scalar- meson fields; General relativity; Dark energy model.
Introduction
Kaluza [2] and Klein [3] have proposed a theory in order to unify the fundamental forces in nature namely gravitation and electromagnetism. This theory in a certain sense resembles the ordinary gravity in free space except that it is phrased in five dimensions instead of four. This theory leads to an interesting possibility known as “cosmological reduction process” in which the scale of extra dimensions becomes so small as to be unobservable by experiencing contraction. Chodos and Detweller [4] and Freund and and Hawking [5] investigated such cosmological models and have shown that the extra dimensions are unobservable due to dynamical contraction. Appelquist et al. [6] has also investigated some cosmological models in five dimensional Kaluza-Klein space-time.
In recent years there has been an immense interest in the investigation of scalar fields because of the fact that they play an important role in cosmology. Physically they represent matter fields with spin less quanta and describe gravitational field in free space. It is also well known that they cause accelerated expansion of the universe. Scalar fields can be classified into two categories. They are mass less (zero mass) scalar fields and massive scalar fields. Mass less scalar fields represents long range interactions and massive scalar fields describe short range interactions. Here we are interested in the zero mass scalar fields. Einstein field equations in the presence of mass less scalar fields for matter distribution can be written as

where Tij is the energy momentum tensor of matter distribution and the mass less scalar field φ satisfies the Klein-Gordon equation

Also we have

which is the matter energy conservation equation.
Cosmological models in the presence of scalar meson fields with different physical matter sources have been investigated by several authors. Ellis [7] and Hawking and Ellis [8] studied FRW models in the presence of mass less scalar fields. Rahaman et al. [9] studied Kantowski-Sachs model in the presence of zero mass scalar fields with a flat potential in Lyraʼs manifold. Venkateswarlu and Pavankumar [10] studied plane symmetric model in the presence mass less scalar fields with cosmic string source while Venkateswarlu and Satish [11] discussed Kantowski –Sachs cosmological model with mass less scalar field in the presence of bulk viscous comic strings. Singh and Rani [12] have investigated Bianchi type-III cosmological models in Lyraʼs geometry in the presence of massive scalar field. Recently, Aditya and Reddy [13] have discussed dynamics of perfect fluid cosmological model in the presence of massive scalar field in f(R,T) gravity. Also Reddy et al. [14] have discussed Bianchi type-II dark energy cosmological model in the presence of scalar-meson fields.
Modern cosmology has been inculcating a lot of interest in the investigation of anisotropic dark energy cosmological models. This is due to the fact that our universe is in a state of accelerated expansion as confirmed by supernova 1a experiment [15-16] and the reason for this being an exotic negative pressure dubbed as anisotropic dark energy (DE). To explain this DE two ways have been suggested. One way is to construct DE models and the other one is to modify general relativity and study their DE models. In this process several modified theories of gravitation have been formulated and anisotropic DE models have been studied by several authors which are abundant in literature. Here we concentrate on anisotropic DE models in the presence of scalar meson fields. Reddy [17] has discussed Bianchi type-V DE model in the presence of zero mass scalar fields while Naidu [18] has investigated Bianchi type-II modified holographic Ricci dark energy cosmological model in the presence of massive scalar field. Very recently, Naidu et al. [19] have obtained Bianchi type-V anisotropic DE model in the presence of attractive massive scalar field.
In the light of the above discussion, it is worth while to discuss five dimensional Kaluza-Klein anisotropic DE model of the universe in the presence of zero mass scalar fields. This is because of the fact that higher dimensional anisotropic DE cosmological models have a significant role in the study of early stages of evolution of the universe immediately after the big bang. Also Guth [20] and Alvarez and Gavela [21] pointed out that due to the presence of an extra dimension production of huge entropy is possible which will help to solve the flatness and horizon problems without invoking the idea of inflation. Hence five dimensional model has been successful in solving some critical problems of big bang cosmology.
Following is the plan of our paper. Sect.2 is devoted to the derivation of Einstein field equations in the presence of mass less scalar meson fields and anisotropic DE in KaluzaKlein space-time. In sec.3 we solve the field equations and present the anisotropic DE Kaluza-Klein cosmological model. In sec.4 we construct all the dynamical parameters of the model and discuss their physical significance.Sec.5 gives summary and conclusions.
Metric and field equations
We consider Kaluza-Klein five dimensional metric in the form
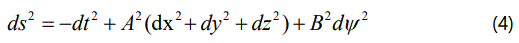
where A and B are functions of cosmic time t and fifth coordinate Ψ is space-like. Unlike Wesson [22], here, the spatial curvature has been taken as zero [23]. The energy momentum tensor of anisotropic DE fluid is given by
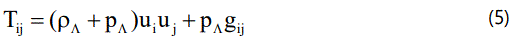
which can be parameterized as
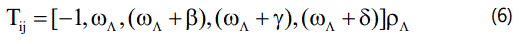
where

Here ρΛ and pΛ are the energy density and pressure of DE fluid, ωΛ is the EoS parameter of DE, β γ, and δ are the skewness parameters which are the deviations from ωΛ along y, z and Ψ axes respectively.
Now using co moving coordinates and the Eqs.(5)-(7) the field equations (1)-(3) for the metric (4) take the form


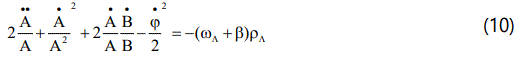
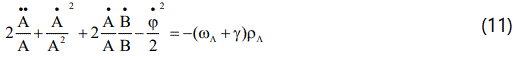



From eqs.(10) and (11), we obtain

In view of Eq.(15), we observe that Eqs.(8)-(14) reduce to the following independent equations:


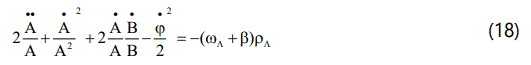


Solutions and the model
It may be observed that the Eqs.(16)-(20) are five independent equations in seven unknowns A,B,φ,ρΛωΛ,β and δ . Hence we are free to choose two physical conditions.
From Eqs.(17), (18) and (15) we, immediately, have

In order solve the equations we use the following physically important conditions:
(i) The shear scalar is proportional to the expansion scalar which leads to a relation between metric potentials given by(Collins [24])

where k >0 is a constant.
(ii) The hybrid expansion law for the average scale factor (Akarsu[1])

Where α1,α2 and a0 a are non-negative constants. Eq.(23) gives the exponential law when α1 = 0 and the power law when α2 = 0.
Now from Eqs.(22) and (23) we get the metric potentials as

From Eqs.(20) and (24) we obtain

Now using Eqs.(24) in Eq.(4) we write down the Kaluza-Klein DE model as
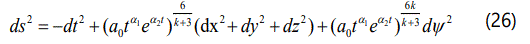
With the scalar field given by Eq.(25) and with the following physical and dynamical parameters which are significant in the discussion of DE cosmological model of the universe.
Physical and dynamical parameters
Spatial volume V of the model (26) is

The average Hubble parameter is

The scalar expansion θ is

The shear scalar σ2 is given by
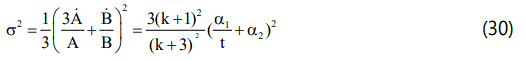
The average anisotropy parameter Δ is given by
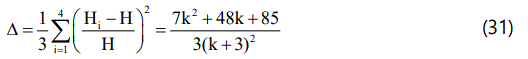
The deceleration parameter q is given by
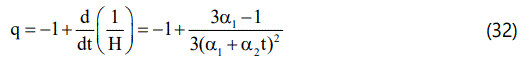
Now from Eqs.(24),(25) and (16) we have DE density as
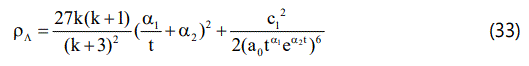
From Eqs.(24), (25),(16), (17) and (33) we determine the EoS parameter of DE as
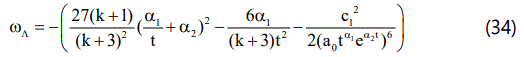
The jerk parameter j(t) is given by

The skewness parameter δ is obtained from Eqs.(17), (19),(24) and (33) as
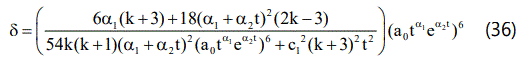
Discussion
We shall now discuss the physical significance of the above cosmological parameters.
The spatial volume increases with cosmic time from zero volume at t=0. Hence the model exhibits a point type singularity at t=o. We can observe that the average Hubble parameter, the expansion scalar and the shear scalar tend to infinity at the initial epoch which imply that all of them diverge at t=0. The average anisotropy parameter is constant and does not vanish which means that the model never becomes isotropic. One can see that when t approaches infinity q = -1 and dH/dt = 0. Then this gives us the greatest value of Hubble parameter and accelerated expansion of the universe. Also ρΛ and δ diverge at t=o and decrease as t increases, i.e; as the universe expands. It may be observed the EoS parameter of DE ωΛ > -1 which means that it should always vary in the quintessence region giving us a quintessence model of the universe. This is, in fact, what we expect for a scalar field model. Also the scalar field becomes a constant for infinitely large t.
In cosmology jerk parameter is useful to describe the DE models close to ΛCDM models. With positive jerk and negative deceleration parameter a transition of the universe occurs from decelerated phase to accelerated phase. At j=1 we have ΛCDM . We can observe here that j is positive and q is negative so that we do have a transition of the model from decelerated to accelerated phase.
Summary and conclusions
This article deals with Kaluza-Klein anisotropic DE model in the presence of a mass less scalar meson field. This model is obtained by solving Einstein field equations using hybrid expansion law and a relation between metric potentials. It is observed that the DE model obtained is a quintessence model. This is due to the fact that we are considering the scalar field model. The model exhibits a translation of the universe from decelerated phase to an accelerating phase. The model has a point type singularity and is always anisotropic. This model will play a vital role in understanding the study of early stages of evolution of the universe immediately after the big bang. The observations made are also in agreement with the predictions of modern cosmology.
References