Abstract

ER = EPR is a conjecture in physics, stating what the entangled particles are connected by a wormhole (Einstein-Rosen bridge or ER bridge for short), and the Einstein-Podolsky-Rosen paradox (or EPR paradox) is an influential thought experiment in quantum mechanics, in which should mean that general relativity and quantum field theory can somehow unify. In pursuit of this goal, we introduce the notion of pseudo-association group (or pa-group). We prove that some groups are pa-groups. As a matter of fact, the pa-group is determined by its commutative idempotent semigroup or ∧-semilattice . These results show some interesting properties, but most interesting is that this paper offers a new and simple but rigorous and abundant proof of the ER=EPR conjecture by using some identity of pa-groups. So, we can say the conjecture is correct.

Keywords: Cosmology; Quantum entanglement; Groups; Lattice

Introduction

As a basic concept of one classic algebra, a group is an algebraic structure consisting of a set of elements equipped with an operation that combines any two elements to form a third element-and the operation satisfies four conditions called the group axioms, namely closure, associativity, identity and invertibility [1]. But what is really interesting is that more general structures are defined by relaxing some of the axioms defining a group [2]. And more importantly, group theory has been made on a fantastically wide range of uses [3-5]. In the bold and shorter essay offers a new algebraic structure, which is called the pseudo-association group (pa-group for short). We discuss some properties and make the commutative diagram for pa-groups. We have to demonstrate the significance of the Λ-semilattice and use it into a result in pa-groups. We will also illustrate it with one example.

In recent years, the theory of everything has increasingly been about quantum gravity. There has been tremendous interest in researching the grand unification of quantum mechanics and gravity in the universe; the quantum entanglement has that honor that has put it in wormhole. Maldacena, Susskind, Cowen and others considered the problem of a related conjecture, i.e., ER= EPR; it is a conjecture in physics, itʼs what it is connected by a wormhole (or known as Einstein-Rosen bridge) [6]; the conjecture was proposed by Leonard Susskind and Juan Maldacena [7] in 2013. Testing the ER = EPR hypothesis to see if it is mathematically consistent with everything else that is known about entanglement and wormholes, so we present fine-structure these two considerations to make a rigorous proof of the conjecture. To know which conjecture was correct, we introduce the notion of pseudo-association group (pa-groups), itʼs a real to mathematical theory to study the problem (i.e., spacetime with quantum entanglement [8]). Wormhole physics, similar to the quantizing gauge field theory has an algebraic structure. Here, the new pa-groups can be used to study some of the peculiar effects of wormhole.

pa-Groups

We introduce a certain pseudo-association principle for the theory of groups. Let Ω be an arbitrary nonempty set. We denote by Pas (Ω) the set of all bijection from Ω to itself. These bijection on Ω are also so-called pseudo-associations, and if Ω finite, this is, of course, the new term. The object Pas (Ω) is called the pa-group on Ω, and the subgroup of Pas(Ω), denoted by Pas(⟨Ω⟩), which we are about to define.

Definition 1

Let Ω be an arbitrary set and let G be a group. We say that G is a Pas (Ω) on Ω is any nonempty subset P ⊆ Pas (Ω) with the following properties:

(PAG 1) P is closed under a pseudo associative binary operation •.
(PAG 2) For each x ∈ P, 1 • x = x = x • 1.
(PAG 3) For each x ∈ P, there exists x^-1 ∈ P such that x • x^-1 = 1 = x^-1 • x.
(PAG 4) For all x, y, z ∈ P, (x • y) • z = x • (z • y).

In addition to abelian groups, Definition 1 allows such objects as the non assocative groups of the integers, the multiplicative groups of the positive rationals, and the groups of n × n nonsingular matrices over fields.

Definition 2

A mirror is called quasi-group G with at identity element 1 with an associative binary operation • defined on G such that there exist 1 ∈ G if it satisfies the axioms:

(QUG 1) 1 • x = x = x • 1 for all x ∈ G and
(QUG 2) 1 • (x • y) = (1 • y) • x = y • x for all x, y ∈ G.

Definition 3

Let (Y, •) be a pa-group and let (Y, ℘) be a topological space. If
•: Y × Y → Y and (x, y) → x • y
be a continuous mapping from the product space (Y × Y, ℘) to the topological space (Y, ℘), where ℘ is product topology of Y. Then we say (Y, ℘, •) is a topological pa-group.

Definition 4

If (f (x, y, z), g (x, y, z)) = 1. Then we say that f (x, y, z) and g(x, y, z) are coprime topological pa-groups (Y, ℘, •) for all x, y, z ∈ Y. Let h (x, y, z), f (x, y, z) and g (x, y, z) be ternary polynomial. Suppose the following condition hold:
(WHT 1) h (x, y, z) = (z • y) • x. (WHT 2) f (x, y, z) = (x • y) • z. (WHT 3) g (x, y, z) = (x • z) • y.

Definition 5

If
(h (x, y, z), f (x, y, z)) = 1 and (h (x, y, z), g(x, y, z)) = 1.
Then
(h (x, y, z), f (x, y, z) • g (x, y, z)) = 1.

Theorem 1

Let G be a group with an associative multiplication and suppose there exists unique element x, y ∈ G such that
x • y = 1 • ( y • x ).
Then G is a commutative group or abelian group.

Proof

This is immediate by Definition 1 and Definition 2. We have
x • y
= (1 • x) • (1 • y) (by (QUG 1))
= (1 • (1 • y)) • x (by (PAG 4))
= (1 • y) • x (by (QUG 2))
= y • x. (by (QUG 2))
Certainly, we have y • x
= (y • x) • 1 (by (QUG 1))
= 1 • (y • x) (by (QUG 1))
= x • y. (by the hypothesis of theorem)

Theorem 2

Let G be a group. Then Pas (Ω) ≅ G only when abelian group conditions are met.

Proof

Let x, y, z ∈ G and Ω. By Theorem 1. Since y • z = z • y. We have
x • (y • z) = (z • y) • x, and we see that
G Route 1: (z • y) • x = z • (x • y) = (x • y) • z and
G Route 2: (z • y) • x = x • (z • y) = (x • y) • z.
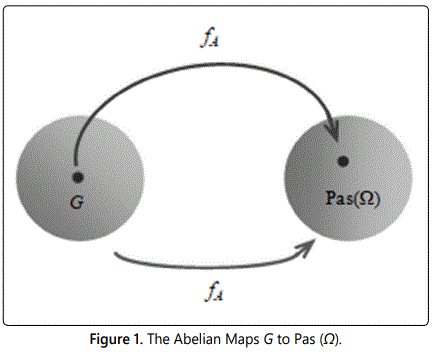
Figure 1 is diagram showing the relevant groups and maps ⟨G, Pas (Ω), abelian⟩, where abelian is a corresponding law, i.e. abelian f_A: G → Pas (Ω).
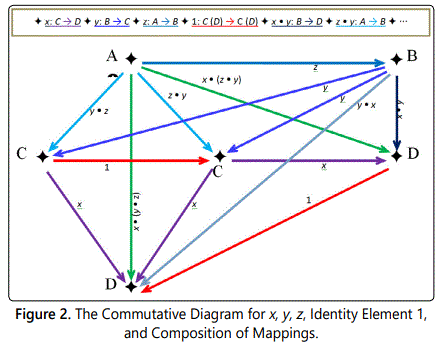
Figure 2 is commutative diagram. Then Pas (Ω) ≅ ≅G

Definition 6

Let G be a nonempty finite set. Suppose the following conditions hold:
(GPA 1) G is an abelian and
(GPA 1) G is a Pas(Ω).
Then we say that G is a group.
Now if X ⊆ Pas(Ω) is any subset, then we define the normalizer of X in Pas(Ω) to be the set
N_P(X) = {p ∈ Pas(Ω) | X ^p = X}.
Here is an Example 1 and its Remark 1.

Example 1

The simple case is n = 3. Let G = {α, β, γ}. We compute the multiplication table, is show in Table 1.

Then (G, •) is an abelian and is a pa-group.

Solution 1 (Proof).

Apply Theorem 2 and this completes the proof.

Solution 2.

Itʼs very easy to compute it directly.

Remark 1

Strictly speaking, in constructing 54 (or 2×3³) combinations of G, but since
a • x = x • α = x for all x ∈ G,
We need to compute that up to 16 (or 2×2³) of combinations.

Theorem 3

Let P be a group of Pas (Ω) and let X ⊆ P be a subset such that
x • y = y • x for all x, y ∈ X.
Then ⟨X⟩ is abelian.

Proof

Let C_P(X) is a subgroup. We can write
C_P(X) = {y ∈ P | x • y = y • x for all x ∈ X}.
It follows that
X ⊆ ∩_x∈X C_p(x).
We conclude that
⟨X⟩ ⊆ C_P(X) and X ⊆ C_P(⟨X⟩).
We know that ⟨X⟩ ⊆ CP(⟨X⟩). Therefore, ⟨X⟩ is abelian.

Corollary 1

Let X, H ⊆ Pas(Ω) be subgroups. If H ⊆ N_P(X). Then
X • H = H • X, and X • H is a subgroup of Pas(Ω).

Corollary 2

Let X be any group and let P be a pa-group. Then P ≅ X.

Theorem 4

Let P ⊆ H ⊆ Pas (Ω). Then H ◁ Pas (Ω).

Proof

Let Pas(Ω) ∕ P be abelian. Since H ∕ P ⊆ Pas(Ω) ∕ P, we have H ∕ P ◁ Pas(Ω) ∕ P, and, in fact
φ: Pas(Ω) → Pas(Ω) ∕ P be the canonical homomorphism, we have
φ((Pas(Ω))ⁿ) = (Pas (Ω) ∕ P)ⁿ, and thus H ◁ Pas(Ω).
One of the major applications of actions is for lattice operation ∧, we give the following Theorem 5.

Theorem 5

Let (S;∧) be the commutative idempotent semigroups, and let
x • y = ¬ x∧y for all x, y ∈ S.
Where ¬ is an order-reversing involution. Then S is a Pas(Ω).

Proof

Let x, y, z ∈ S and 1 is the greatest element. Then the binary operation ∧ is closed in this semilattice S.
We prove (PAG 2). By Theorem 1. Then
1 • x
= ¬ 1 ∧ (¬ x ∧ 1)
= (¬ x ∧ 1) ¬ 1
= ¬ x ∧ (1 ¬ 1)
= ¬ x ∧ 1
= x • 1.
Obviously, x • 1 = x = x ∧ 1.
Using the same method, we prove (PAG 3). Then
x • x ^-1
= ¬ 1 ∧ (¬ x^-1 ∧ x)
= (¬ 1 ∧ ¬ x^-1) ∧ x
= ¬ (1 ∧ x^-1) ∧ x
= x^-1• x.
Clearly also x^-1• x = 1 = x^-1 ∧ x.
We prove (PAG 4). Then
x • (z • y)
= ¬ x ∧ (¬ z ∧ y)
= (¬ x ∧ ¬ z) ∧ y
= y ∧ (¬ x ∧ ¬ z)
= (y ∧ ¬ x) ∧ ¬ z
= (x • y) • z.
This proof is now complete.

Corollary 3

Let S be the semilattice of commutative idempotent semigroups and assume that
x • y = ¬ x ∧ y for all x, y ∈ S.
Then S is a quasi-group G_q.

Conjecture and Proof

This section describes the structure of the proof of the ER = EPR conjecture. Raamsdonkʼs essay, originally published in the General Relativity and Gravitation [8] has been concerned; this illustrates the wormhole compatibility with the quantum entanglement. This conjecture ER= EPR is an extrapolation of the observation that a maximally extended AdS-Schwarzschild black hole, which is a nontraversable wormhole, is dual to a pair of maximally entangled thermal conformal field theories via the AdS/CFT correspondence. In fact, a similar idea was actually first proposed by Friedwardt Winterberg [9]. Maldacena discovered that the boundary and the bulk (or known as Anti-de Sitter space (AdS)) are completely equivalent. Susskind and Tadashiʼs [10] paper, provided a strong mathematics tool for the quantum entanglement. But, we examine that conjecture from different point of view, which is group theory, and give a new proof. It gives us some clues where to look structure of wormhole.

The following conjecture is the most natural question and is the most basic conjecture in modern physics.

Theorem 6 (Maldacena-Susskindʼs Conjecture)

If any two particles are connected by entanglement. Then they are effectively joined by a wormhole. And vice versa: the connection that physicists call a wormhole is equivalent to entanglement.

Proof

Note that there is some association between the wormhole and quantum entanglement to do mathematics. There associations, which mathematically from that the pa-group, as mentioned Theorem 2, we can demonstrate that the quantum computing is possible, i.e., as shown in figure 2, quantum can work (or compute) in there two paths (e.g. G Route 1 and G Route 2 in proof of Theorem 2) in both at the same time, to perform a series of native operations in one trip to the wormhole, the proposed scheme can provide highly stable and accurate results.

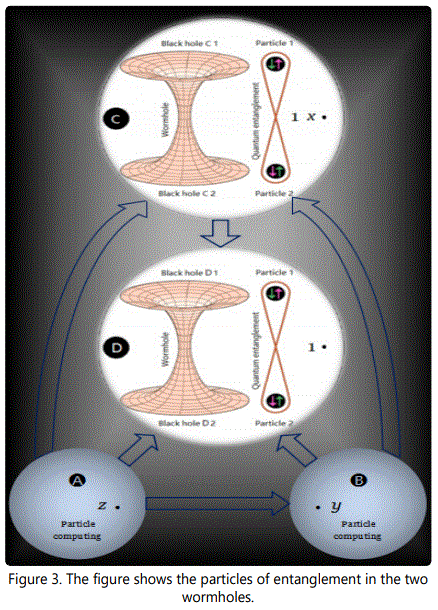
For explain the phenomenon of entanglement, we find four interconnected things, that is, the notation A, B, C and D in (Figure 3). Physics say, can be related in six ways, C and D be two wormholes; mathematics say, C and D be multiply-connected spaces. The proof of Theorem 2 provides the accreting black hole for their existence in universe. More broadly, a black hole can accrete matter into itself as the matter falls or is pulled towards it. The accreting material then orbits around the black hole, forming an accretion disk. The pattern is shown in figure 2 and figure 3 for the black hole — wormhole — quantum entanglement — particle computing — which has three particles x, y and z (e.g. the three pions, (π⁺, π⁰, π^–)) as its operations in orbit. The arrows indicate the direction of transformation of the particles in universe. The wormhole may be expanding and contracting - i.e. wormhole computing. In some rhythmic way is caused by quantum entanglement. Namely, they are different ways of describing the same underlying reality.

Think of a three-dimensional internal space C and D as anti-de Sitter space (AdS), it is commonly referred to as the bulk. The other model is also filled with elementary particles in A and B as particle computer and communications, the boundary particles y and z into the vortex of a black hole and in the wormhole for calculations, just like a computer. There are good quantal reasons why wormhole may seem to have a certain priority for us, because entanglement lets the measurement of one particle instantaneously determine the state of a partner particle, no matter how far away it may be - even on the other side of the Milky Way. As far as the pagroup, really both wormhole functions Ω(x) and entanglement functions ζ (x) are, on a par. An integer n, define a function θ: Ω (x) → ζ (x) is said to be a class function on pa-group. It follows that

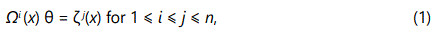
Where i stands for some internal index counting different species of particles and j stands for some external index counting different species of particles. For example, we have the pa-group for the pions (π⁺, π⁰, π^–) on three states (i = 1, 2, 3). This map θ is surjective since Ω (x) generates ζ (x), i.e. the wormhole is expanding and contracting. So, the ER = EPR conjecture is true.

Remark 2

We are using figure 3 to explain our ideas, we have two wormholes makes it possible for the particles of entanglement, and we can have a physical moment when we decide how we want to calculate it. For pa-groups to explain the distinction between worm hole and entanglement has lost. Pions, as a reasonable counterpoint to the pa-group of wormhole, has played equally important role, it may be that for the extreme conditions at the Big Bang a description. In a nutshell, ER=EPR.

Conclusions

In practice, of course, the pseudo-association law, introduced by the pa-BCL⁺ algebras [11], but this paper modified to take advantage of the peculiarly available groups. The problem of homomorphism had been overcome in pa-groups. Interestingly, pa-groups have a close relationship to ∧-semilattice. Deserved to be mentioned, as application of the theory of groups we can from quantum entanglement point of view it is important to research that this mysterious ER = EPR questions have on our motivation via the pa-groups, getting down to the article.

References

1. Herstein IN. Topics in algebra. 2nd edition. New York NY: John Wiley & Sons Inc; 2016.   
2. Denecke K, Wismath SL. Universal algebra and applications in theoretical computer science. 1st edition. Boca Raton, London, NewYork, Washington DC: Chapman & Hall, CRC Press; 2002.   
3. Weinberg S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. 1st edition. New York NY: John Wiley & Sons Inc; 1972.   
4. Miller Jr W. Symmetry groups and their applications. 1st edition. New York NY: Academic Press; 1972.   
5. Seress A. An introduction to computational group theory. Notices of the AMS. 1997; 44: 671-679.   
6. Cowen R. The quantum source of space-time. Nature. 2015; 527: 290-293. doi: 10.1038/527290a   
7. Maldacena J, Susskind L. Cool horizons for entangled black holes. Fortsch. Phys. 2013; 61: 781-811. doi: 10.1002/prop.201300020   
8. Raamsdonk MV. Building up spacetime with quantum entanglement. Gen. Rel. Grav. 2010; 42: 2323- 2329. doi: 10.1007/s10714-010-1034-0   
9. Winterberg F. Teichmller space interpretation of quantum mechanics. Annales de la Fondation Louis de Broglie. 2013; 38: 129-137.   
10. Ryu S, Takayanagi T. Quantum entanglement and holography. Phys. Rev. Lett. 2006; 96: 181602.   
11. Liu Y. pa-BCL+ algebras and groups. Applied Mathematics & Information Sciences. 2017; 11: 891-897. doi: 10.18576/amis/110329