Abstract

Considering entropy correction terms resulting from loop quantum gravity, we investigate an interacting agegraphic dark energy model. The connection between such a model and a tachyon scalar field which couples to matter in Lagrangian is studied. We reconstruct the related potential of tachyon field and find its dynamics in the Universe. Also, we discuss the implications of this entropy-corrected agegraphic dark energy model.

Keywords: Dark energy; Chameleon; Tachyon; Agegraphic; Entropy corrected

Introduction

Recent cosmological observations demonstrate that our Universe is in an accelerated expansion phase [1-6]. We ascribe this acceleration to a mysterious matter with negative pressure called dark energy (DE). Different DE models have been proposed in literature [7-17]. Among them the holographic DE (HDE) and agegraphic DE (ADE) models are of particular interest because they arise from a more fundamental theory, dubbed quantum gravity. Choosing an appropriate length scale is one of the most important features of these models. From this point of view, ADE is preferable, because the HDE suffers from the causality problem that in turn arise from choosing event horizon as the length scale [18-19]. The energy density of ADE models is derived from the energy density of metric fluctuations of Minkowski spacetime as [20-22]

in which M_p, is the reduced Planck mass and the numerical factor 3n², is introduced to parameterize some uncertainties. In ADE models we have two options. One can choose the age of the Universe as the length scale in a model called original ADE (OADE) [23]. Also, in a new ADE (NADE) model, the conformal age instead of the cosmic age can be chosen [16]. Therefore there is not any causality problem here.

A key point in deriving the energy density of HDE and ADE, is the relation between entropy and area of black holes in Einstein gravity [14]. This relationship can be modified due to some quantum considerations in standard general relativity. There are two modifications, the power-law entropy corrections [24-25] and the logarithmic entropy corrections [26-27]. In the logarithmic entropy corrected ADE (LECADE) model, the energy density in Eq. (1), is modified as

in which α and β are dimensionless constants of order unity. It is obvious that for large t, the correction terms can be negligible and the LECADE model reduces to the ordinary ADE model.

On the other hand, interaction between the dark sectors of the Universe is important, because it can resolve or at least alleviate a few cosmological problems such as coincidence problem [28-33]. So, the interaction between ADE and dark matter (DM), has been investigated in recent past [34-41].

Also, much attempts have been done to reconstruct scalar field DE models, from HDE and ADE [42-46]. In some of them the coupling between the scalar field and DM Lagrangian, called chameleon, has been considered [47-49]. Tachyon scalar field motivated from string theory is a especial scalar field which can explain the whole history of the Universe from inflation to late time acceleration [50-59]. The tachyon field reconstruction of HDE and ADE models has been studied separately in some works [60-64].

In this manuscript, an interacting ADE model with the logarithmic correction in the entropy-area relation is considered. In this context a chameleon-tachyon cosmology, i.e., a tachyon scalar field coupled to matter is reconstructed. This work is a complementary of the articles [39, 61-64].

Chameleon-Tachyon Reconstruction of Original Lecade (Olecade)

Assuming the energy density of the OLECADE of the form Eq. (2), and choosing the age of the Universe T, as the time scale, we have

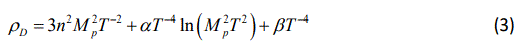
where T is defined as

Using Eq.(3) and defining Ω_D=ρ_D/(3M_p²H²), we reach to

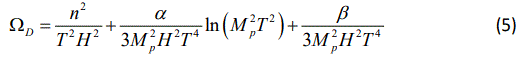
Now, we consider the chameleon cosmology with a tachyon potential in the action given by

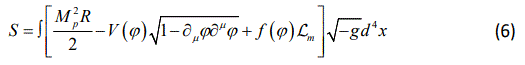
where R is Ricci scalar and V(ϕ) is the tachyonic potential. The matter Lagrangian L_m is modified as f(ϕ)L_m, which shows the interaction between the matter content of the Universe and tachy on field.

We consider the spatially flat Friedmann-Robertson-Walker (FRW) Universe with the line element

With the variational approach one can reach to the following field equations

where H = ȧ /a, is the Hubble parameter and dot means derivative with respect to time t. Also, we have assumed that a perfect fluid with the equation of state p_m=yρ_m has filled the Universe. ρ_tac and ρ_tac are the energy density and pressure of the tachyon field, respectively

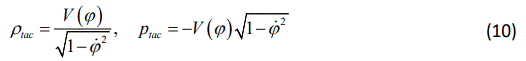
Then, we define the fractional energy densities as

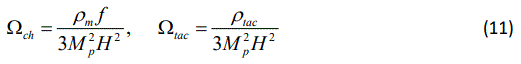
where the subscript ch stands for chameleon and Ω_ch=Ω_mf. So, the Friedmann equation (8), can be written as

In all interacting models the densities of dark matter (DM) and DE, violate the independent conservation law. The form of interaction term is an assumption and is not unique, but usually it expresses as a combination of the DM and DE densities and simultaneously is linear in terms of the Hubble parameter. Here, in one hand, we are assuming that the tachyon field plays the role of DE, as an ADE and on the other hand plays the role of DM, as a chameleon field coupled to matter. Assuming the Universe filled with cold DM (CDM), i.e. p_m=0, the dark sectors in our model satisfy

and

where ρ_ch=ρ_mf. The very interesting feature of our model is that the interaction term Q, appears naturally and without any assumption. With some calculation one can find that Q=∈ρ_mf, with ∈=1-3γ, which is directly dependent to the chameleon coupling function f(ϕ) and ρ_m DM density and indirectly to the Hubble parameter.

Now, we differentiate Eq.(3) with respect to time and obtain

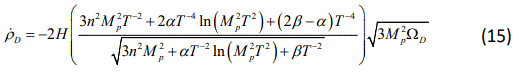
Replacing ρ_tac in Eq.(14), with the expression above we obtain the equation of state parameter of the DE component as

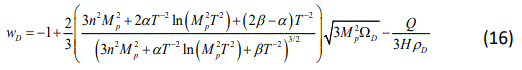
in which we have used Eq.(5). On the other hand, we take the time derivative of Eq.(5) and using Ω̇_D=Ω#700;_DH we reach to

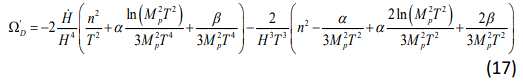
where the prime denotes differentiation with respect to the e-folding parameter, In a. Differentiating Eq.(8) with respect to time and using Eqs. (11), (12), (13) and (15) we obtain

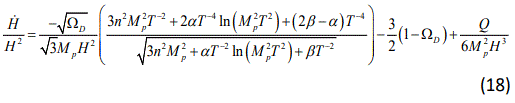
Substituting the expression above in Eq.(17) yields to

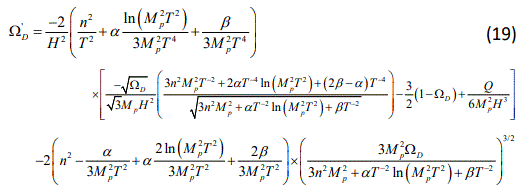
We complete our chameleon-tachyon reconstruction of OLECADE model by rewriting the potential and kinetic term of tachyon scalar field as

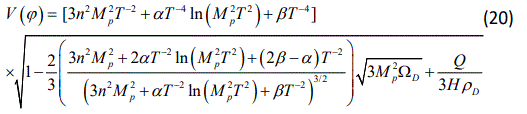
and

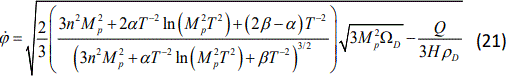
in which we have used Eq.(16) and the relation w_tac=ϕ̇²-1. With attention to ϕ̇=ϕʼH, we find

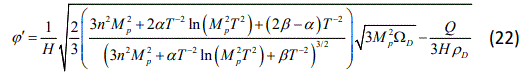
Integrating the above equation results

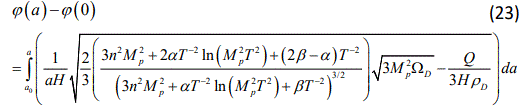
Here a₀, is the present value of the scale factor. Thus, we have organized an interacting logarithmic entropy corrected agegraphic chameleon-tachyon dark energy model and reconstructed the tachyon potential and obtained its dynamics. It is interesting to note that in the case α = β = 0, our results reduce to the corresponding ones in [64].

Chameleon-Tachyon Reconstruction of New Lecade (Nlecade)

In NLECADE, the length scale is assumed to be the conformal time n, which is introduced as

So, Eq.(2) is written as

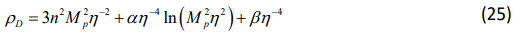
Also, we can obtain the corresponding dimensionless density parameter as

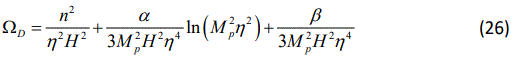
Differentiating Eq.(25) with respect to the cosmic time t, one can reach

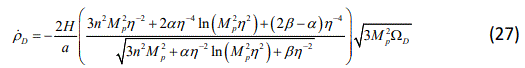
Inserting Eq.(27) into Eq.(14), we get

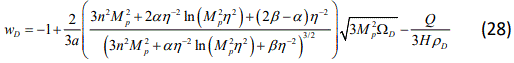
On the other hand, differentiating Eq.(26) with respect to t, we obtain

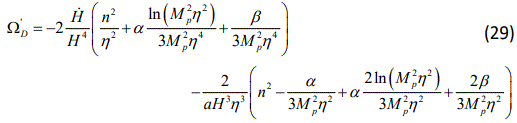
where we have used ϕ̇_D=ϕʼ_DH. Also, in a similar way to the OLECADE and using Eq.(27), one can get

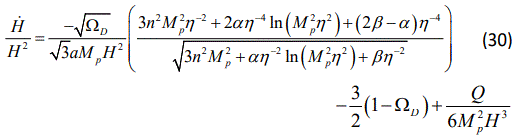
Substituting the latter in Eq.(29) and using Eq.(26), we reach to

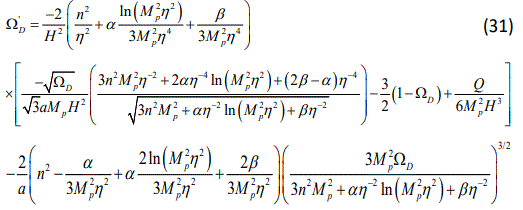
The reconstruction will be completed if we rewrite tachyonic potential and its kinetic term as

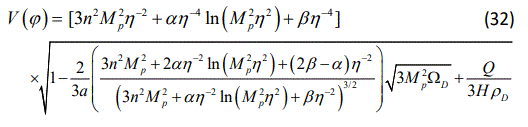
and

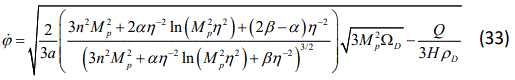
In a similar approach to the prior section we find that

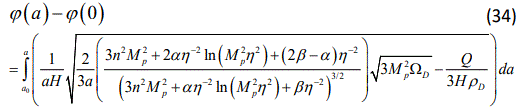
Again, it is easy to check that in the case α = β = 0, all the above relations reduce to those discussed in [64].

Cosmological implications of Lecade Chameleon-Tachyon Models

To deal with the cosmological implications we calculate two important cosmological parameters in our model. The deceleration parameter is defined as

Substituting Eqs.(18) and (30) in the above relation, we obtain

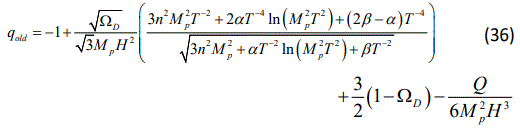
for OLECADE and

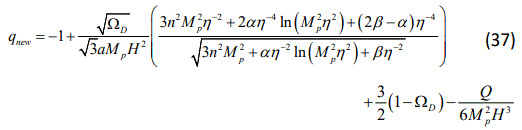
for NLECADE model.

On the other hand, the effective equation of state parameter can be calculated as follow

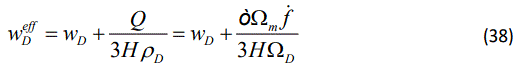
where using Eqs.(16) and (28) we obtain

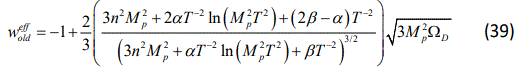
and

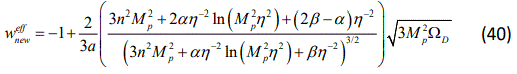
Summary and Discussion

Here, we investigated a logarithmic entropy corrected model of OADE and NADE and studied the correspondence between them and a chameleon-tachyon DE model, i.e., a tachyon scalar field which is coupled to matter Lagrangian. We reconstructed the tachyonic potential in each case and obtained its evolution with respect to time and scale factor parameter. On the other hand, we calculated the deceleration parameter and the effective equation of state parameter of both models to deal with the cosmological implications of our model.

References

1. Larson D, Dunkley J, Hinshaw G, et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Power Spectra and WMAPDerived Parameters. Astrophys. J. Suppl. Ser. 2011; 192: 16. doi: 10.1088/0067-0049/192/2/16   
2. Xu L, Wang Y. Cosmography: Supernovae Union2, Baryon Acoustic Oscillation, observational Hubble data and Gamma ray bursts. Phys. Lett. B. 2011; 702: 114-120. doi: 10.1016/j.physletb.2011.06.091   
3. Kowalski M, Rubin D, Aldering G, et al. Improved Cosmological Constraints from New, Old and Combined Supernova Datasets. Astrophys. J. 2008; 686: 749-778. doi: 10.1086/589937   
4. Frieman J, Turner M, Huterer D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008; 46: 385-432. doi: 10.1146/annurev.astro.46.060407.145243   
5. Vitagliano V, Xia JQ, Liberati S, Viel M. High-Redshift Cosmography. J. Cosmol. Astropart.Phys. 2010; 3: 005. doi: 10.1088/1475-7516/2010/03/005   
6. Eisenstein DJ, Zehavi I, Hogg DW, et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005; 633: 560-574. doi: 10.1086/466512   
7. Caldwell RR, Dave R, Steinhardt RJ. Cosmological Imprint of an Energy Component with General Equation of State. Phys. Rev. Lett. 1998; 80(8): 1582. doi: 10.1103/PhysRevLett.80.1582   
8. Armendariz-Picon C, Mukhanov V, Steinhardt PJ. Essentials of k-essence. Phys. Rev. D. 2001; 63: 103510. doi: 10.1103/PhysRevD.63.103510   
9. Sen A. Remarks on Tachyon Driven Cosmology. Phys. Scr. T. 2005; 117: 70. doi: 10.1238/Physica.Topical.117a00070   
10. Caldwell RR. A Phantom Menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett B. 2002; 545: 23-29. doi: 10.1016/S0370-2693(02)02589-3   
11. Feng B, Wang XL, Zhang XM. Dark Energy Constraints from the Cosmic Age and Supernova. Phys. Lett.B. 2005; 607: 35-41. doi: 10.1016/j.physletb.2004.12.071   
12. Kamenshchik A, Moschella U, Pasquier V. An alternative to quintessence. Phys. Lett. B. 2001; 511: 265-268. doi: 10.1016/S0370-2693(01)00571-8   
13. Bengochea GR. Observational information for f(T) theories and Dark Torsion. Phys. Lett. B. 2011; 695: 405-411. doi: 10.1016/j.physletb.2010.11.064   
14. Cohen AG, Kaplan DB, Nelson AE. Effective Field Theory, Black Holes, and the Cosmological Constant. Phys. Rev. Lett. 1999; 82(25): 4971. doi: 10.1103/PhysRevLett.82.4971   
15. Li B, Sotiriou TP, Barrow JD. f(T) Gravity and local Lorentz invariance. Phys. Rev. D. 2011; 83: 064035. doi: 10.1103/PhysRevD.83.064035   
16. Wei H, Cai RG. A New Model of Agegraphic Dark Energy. Phys. Lett. B. 2008; 660(3): 113-117. doi: 10.1016/j.physletb.2007.12.030   
17. Gao C, Wu F, Chen X, Shen YG. Holographic dark energy model from Ricci scalar curvature. Phys. Rev. D. 2009; 79(4): 043511. doi: 10.1103/PhysRevD.79.043511   
18. Guberina B, Horvat R, Nikolic H. Nonsaturated Holographic Dark Energy. J. Cosmol. Astropart.Phys. 2007; 1: 012. doi: 10.1088/1475-7516/2007/01/012   
19. Wei H. Entropy-Corrected Holographic Dark Energy. Commun. Theor. Phys. 2009; 52: 743. doi: 10.1088/0253-6102/52/4/35   
20. Karolyhazy F. Gravitation and quantum mechanics of macroscopic objects. Nuovo. Cim. A. 1966; 42(2): 390-402. doi: 10.1007/BF02717926   
21. Maziashvili M. Space-Time In Light Of Károlyházy Uncertainty Relation. Int. J. Mod. Phys. D. 2007; 16(9): 1531-1539. doi: 10.1142/S0218271807010870   
22. Maziashvil M. Cosmological implications of Károlyházy uncertainty relation. Phys. Lett. B. 2007; 652(4): 165-168. doi: 10.1016/j.physletb.2007.07.008   
23. Cai RG. A Dark Energy Model Characterized by the Age of the Universe. Phys. Lett. B. 2007; 657: 228-231. doi: 10.1016/j.physletb.2007.09.061   
24. Das S, Shankaranarayanan S, Sur S. Power-law corrections to entanglement entropy of horizons. Phys. Rev. D. 2008; 77: 064013. doi: 10.1103/PhysRevD.77.064013   
25. Sheykhi A, Jamil M. Power-Law Entropy Corrected Holographic Dark Energy Model. Gen. Rel. Grav. 2011; 43: 2661-2672. doi: 10.1007/s10714-011-1190-x   
26. Kaul RK, Majumdar P. Logarithmic Correction to the Bekenstein-Hawking Entropy. Phys. Rev. Lett. 2000; 84(23): 5255. doi: 10.1103/PhysRevLett.84.5255   
27. Amani AR, Sadeghi J, Farajollahi H, Pourali M. Logarithmic entropy corrected holographic dark energy with nonminimal kinetic coupling. Can. J. Phys. 2011; 90(1): 61-66. doi: 10.1139/p11-140   
28. Karwan K. The Coincidence Problem and Interacting Holographic Dark Energy. JCAP. 2008; 0805: 011. doi: 10.1088/1475-7516/2008/05/011   
29. Wang S, Zhang Y. Alleviation of cosmic age problem in interacting dark energy model. Phys. Lett. B. 2008; 669(3-4): 201-205. doi: 10.1016/j.physletb.2008.09.055   
30. Sadjadi HM, Alimohammadi M. Cosmological coincidence problem in interacting dark energy models. Phys. Rev. D. 2006; 74: 103007. doi: 10.1103/PhysRevD.74.103007   
31. Hu B, Ling Y. Interacting dark energy, holographic principle, and coincidence problem. Phys. Rev. D. 2006; 73(12): 123510. doi: 10.1103/PhysRevD.73.123510   
32. Berger MS, Shojaei H. Interacting dark energy and the cosmic coincidence problem. Phys. Rev. D. 73, 2006; 73(8): 083528. doi: 10.1103/PhysRevD.73.083528   
33. Cai RG, Wang A. Cosmology with Interaction between Phantom Dark Energy and Dark Matter and the Coincidence Problem. JCAP. 2005; 0503: 002. doi: 10.1088/1475-7516/2005/03/002   
34. Wei H, Cai RG. Interacting agegraphic dark energy. Eur. Phys. J. C. 2009; 59: 99-105. doi: 10.1140/epjc/s10052-008-0799-8   
35. Sheykhi A. Interacting agegraphic dark energy models in non-flat universe. Phys. Lett. B. 2009; 680: 113-117. doi: 10.1016/j.physletb.2009.08.051   
36. Sheykhi A. Interacting new agegraphic dark energy in nonflat Brans-Dicke cosmology. Phys. Rev. D. 2010; 81: 023525. doi: 0.1103/PhysRevD.81.023525   
37. Sheykhi A, Bagheri A, Yazdanpanah MM. Interacting agegraphic quintessence dark energy in non-flat universe. JCAP. 2010; 1009: 017. doi: 10.1088/1475-7516/2010/09/017   
38. Zhang L, Cui J, Zhang J, Zhang X. Interacting Model of New Agegraphic Dark Energy: Cosmological Evolution and Statefinder Diagnostic. Int. J. Mod.Phys. 2010; 19(1): 21-35. doi: 10.1142/S0218271810016245   
39. Karami K, Khaledian MS, Felegary F, Azarmi Z. Interacting new agegraphic tachyon, K-essence and dilaton scalar field models of dark energy in nonflat universe. Phys. Lett. B. 2010; 686: 216-220. DOI: 10.1016/j.physletb.2010.02.075   
40. Lemets OA, Yerokhin DA, Zazunov LG. Interacting agegraphic dark energy models in phase space. JCAP. 2011; 01: 007. doi: 10.1088/1475-7516/2011/01/007   
41. Saaidi K, Sheikhahmadi H, Mohammadi AH. Interacting new agegraphic dark energy in a cyclic universe. Astrophys. Space Sci. 201; 338(2): 355-361. doi: 10.1007/s10509-011-0944-y   
42. Zhang X. Reconstructing holographic quintessence. Phys. Lett. B. 2007; 648: 1-7. doi: 10.1016/j.physletb.2007.02.069   
43. Karami K, Khaledian MS, Jamil M. Reconstructing interacting entropycorrected holographic scalar field models of dark energy in the non-flat universe. Phys. Scr. 2011; 83: 025901. doi: 10.1088/0031-8949/83/02/025901   
44. Yang WQ, Wu YB, Song LM, et al. Reconstruction of New Holographic Scalar Field Models of Dark Energy in Brans–Dicke Universe. Mod. Phys. Lett. A. 2011; 26: 191-204. doi: 10.1142/S0217732311034682   
45. Wu JP, Ma DZ, Ling Y. Quintessence reconstruction of the new agegraphic dark energy model. Phys. Lett. B. 2008; 663: 152-159. doi: 10.1016/j.physletb.2008.03.071   
46. Sheykhi A. Holographic scalar field models of dark energy. Phys. Rev. D. 2011; 84: 107302. doi: 10.1103/PhysRevD.84.107302   
47. Chattopadhyay S, Pasqua A, Khurshudyan M. New holographic reconstruction of scalar-field dark-energy models in the framework of chameleon Brans-Dicke cosmology. Eur. Phys. J. C. 2014; 74: 3080. doi: 10.1140/epjc/s10052-014-3080-3   
48. Saaidi K, Sheikhahmadi H, Golanbari T, Rabiei SW. On the holographic dark energy in chameleon scalar-tensor cosmology. Astrophys. Space Sci. 2013; 348: 233-240. doi: 10.1007/s10509-013-1491-5   
49. Setare MR, Jamil M. Holographic dark energy in Brans–Dicke cosmology with chameleon scalar field. Phys. Lett. B. 2010; 690(1): 1-4. doi: 10.1016/j.physletb.2010.05.002   
50. Sen A. Rolling Tachyon. J. High Energy Phys. 2002; 04: 048. doi: 10.1088/1126-6708/2002/04/048   
51. Sen A. Tachyon Matter. J. High Energy Phys. 2002; 07: 065. doi: 10.1088/1126-6708/2002/07/065   
52. Mazumdar A, Panda S, Perez-Lorenzana A. Assisted inflation via tachyon condensation. Nucl. Phys. B. 2001; 614: 101-116. doi: 10.1016/S0550-3213(01)00410-2   
53. Feinstein A. Power-law inflation from the rolling tachyon. Phys. Rev. D. 2002; 66(6): 063511. doi: 10.1103/PhysRevD.66.063511   
54. Sami M. Implementing Power Law Inflation with Tachyon Rolling on the Brane. Mod. Phys. Lett. A. 2003; 18(10): 691-697.   
55. Padmanabhan T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D. 2002; 66: 021301. doi: 10.1103/PhysRevD.66.021301   
56. Farajollahi H, Ravanpak A, Fadakar GF. Holographic dark energy in chameleon tachyon cosmology. Astrophys. Space Sci. 2011; 336(2): 461-467. doi: 10.1007/s10509-011-0779-6   
57. Farajollahi H, Ravanpak A. Tachyon field in intermediate inflation on the brane. Phys. Rev. D. 2011; 84: 084017. doi: 10.1103/PhysRevD.84.084017   
58. Farajollahi H, Salehi A, Tayebi F, Ravanpak A. Stability Analysis in Tachyonic Potential Chameleon cosmology. JCAP. 2011; 05: 17-37. doi: 10.1088/1475-7516/2011/05/017   
59. Gibbons GW. Cosmological Evolution of the Rolling Tachyon. Phys. Lett. B. 2002; 537: 1-6. doi: 10.1016/S0370-2693(02)01881-6   
60. Granda LN. Reconstructing the potentials for the quintessence and tachyon dark energy, from the holographic principle. Int. J. Mod. Phys. D. 2009; 18: 1749-1764. doi: 10.1142/S0218271809015291   
61. Farooq MU, Rashid MA, Jamil M. Thermodynamics of Modified Chaplygin Gas and Tachyonic Field. Int. J. Theor. Phys. 2010; 49: 2278.   
62. Sheykhi A. Interacting agegraphic tachyon model of dark energy. Phys. Lett. B. 2010; 682: 329-340. doi: 10.1016/j.physletb.2009.11.034   
63. Jamil M, Sheykhi A. Interacting Entropy-Corrected Agegraphic-Tachyon Dark Energy. Int. J. Theor. Phys. 2011; 50(3): 625-636. doi: 10.1007/s10773-010-0585-x   
64. Farajollahi H, Ravanpak A, Fadakar G. Interacting agegraphic dark energy model in tachyon cosmology coupled to matter. Phys. Lett. B. 2011; 711: 225-231. doi: 10.1016/j.physletb.2012.04.001