Abstract

An expert of the Navier-Stokes Equation requested one solution or example, of a solution to the Navier Stokes Equation. Using Astrotheology variables published in many paper by this author, we provide a solution to Navier-Stokes.

Keywords: Navier-Stokes; Astrothoelogy; Reynoldʼs Number; Youngʼs modulus

Introduction

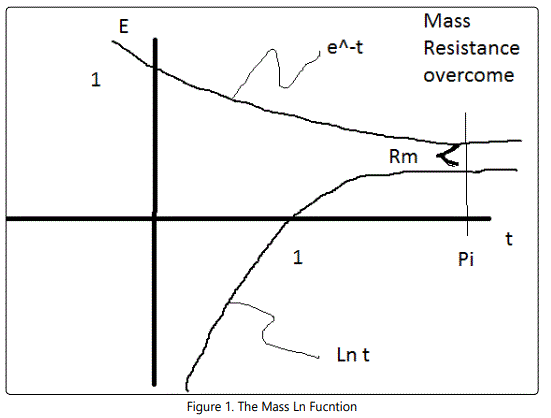
In this brief paper, we provide a solution to the Navier -Stokes Equation [1-3]. The answer to the variables lie in AT Math (Astrotheology, Cusackʼs Universe) shown in (Figure 1).

ρ(∂v/∂t +v ·∇v)=∇P+∇T +F
ρ=4/π=127.3
v=a=sin 45°=cos 45°=1/√2
P=S.F/ Area
S.F. =8/3=2.667
R=1
θ=Reynoldʼs Number=0.402 rads=23.03 degrees
T=Youngʼs modulus =(π-e)=0.4233=cuz
F=0
127.3(1/√2 +1/√2 ×1/√2 cos(0.402) )= 8/3/(π(1)²) + ∇(0.4233)+0
127.3(116.72)=-0.8489 + ∇ (0.4233) cos (0.402)
23.373=0.4233 (0.9202) ∇
Let:
∇= (∂/∂x + ∂/∂y+ ∂/dz)
∂/∂x =∂/∂y=∂/dz
∇=1/0.167=1/γ (monatomic gas)
3 (∂/∂x)=1/(1/6)
∂/∂x= 2= dM/dt
(2+x)³= x³+6x²+12 x +8=0
x=-1
x= 1/2 i(√3+5i)
Let i=-.0618
=4.196
Ln x=0.868=sin 1
Ln x =Ln 1/ Ln 2.368=Ln 1-Ln 23.68
e^{Ln x}=e^{-Ln 23.68}
x=e-sin 1
=1/e^{sin 1}
=e^-1/M Where M=118 Number of elements in the Periodic Table.
So (2+1) = 3=Eigen Value, speed of light
(2+x)= 2+13.03=15.03= Mass Gap=1/G

Conclusion

This is the solution to the Navier Stokes Equation.

Acknowledgements

None.

Conflict of interest

The author declares that there is no conflict of interest.

References

1. Cusack P. Astro-Theology, Cusacks Universe. J. Phys. Math. 2016; 7(2): 8.   
2. Steward I. In Pursuit of the Unknown. NY 2012.   
3. Cusack P. The Universal Vector. Ope Acc J. Math Theo Phys.2018; 1(5): 186-190. doi: 10.15406/oajmtp.2018.01.00032