Abstract

Temperature dependence of the IR frequency and the damping constant (FWHM) of the ν₄(1440 cm^-1) NH₄+and ν₄(1084 cm^-1) ND₄+ modes, are calculated for the metal formate frameworks (MOFs) of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, respectively, by using the experimental data from the literature. By assuming the IR frequency of the ν₄ mode as an order parameter, its temperature dependence is calculated close to the phase transition (TC=191 K) in the NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ by the molecular field theory. The temperature dependence of the damping constant of the ν₄ (NH₄+) IR mode is also calculated by means of the pseudospin-phonon coupled (PS) and the energy fluctuation (EF) models for these metal formate frameworks. The damping constant due to both models (PS and EF) is fitted to the observed FWHM data of the ν₄ (NH₄+) IR mode from the literature at various temperatures close to TC in the MOFs studied.

Our results show that the molecular field theory is adequate for the temperature dependence of the IR frequency and also the PS model explains the observed behaviour of the FWHM for the ν₄(NH₄+) mode in NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃.

Keywords: IR frequency; Damping constant (FWHM); Molecular field theory; Pseudospin-phonon coupled (PS) model; MOFs.

Introduction

Metal formate frameworks (MOFs) with the ammonium cations, NH₄M(HCOO)₃ for M=Mn, Co and Ni compounds have been studied extensively by using X-ray diffraction, dielectric, differential scanning calorimetry (DSC) and magnetic measurements [1-5]. In particular, infrared (IR) and Raman bands in these structures have been assigned [3,4] in order to investigate both temperature- and pressure- induced phase transition mechanism including order-disorder, displacive transitions and H-bonds studies [6-9]. It has been pointed out that H-bonds and ordering of the ammonium ions play an important role in the mechanism of the phase transition (order-disorder) and multiferroelectric behavior of this family of compounds at low temperatures [5]. Dielectric properties of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, DSC study of the deuterated sample, temperature-dependent of Raman scattering and infrared (IR) studies of both compounds, high-pressure Raman scattering of ND₄Zn(DCOO)₃ and DFT calculations of both structures have been reported to investigate their structural phase changes [5]. From the DSC measurements of ND₄Zn(DCOO)₃ an anomaly occurs at around 191 K upon heating and 190 K upon cooling, which is similar as observed for other NH₄M(HCOO)₃ formates with M=Mn, Co, Fe, Ni, Zn and Mg [1-4], indicating a second order, reversible phase transition, as pointed out previously [5]. On the other hand, for NH₄Zn(HCOO)₃ the phase transition was reported to be 192 K in the heating mode [1,2] which shows that the isotope effect for this compound is very small [5]. Anomaly was attributed to the onset of a ferroelectric order in the low temperature phase and the ferroelectricity of NH₄Zn(HCOO)₃ was confirmed by the presence of a dielectric hysteresis loop [1,2,10], as indicated previously [5].

The temperature dependence of the Raman and IR bands of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ regarding internal vibrations of the ammonium and formate ions, and the lattice vibrations can be studied, as observed experimentally [5] in terms of their frequency shifts and FWHM. In particular, the IR frequency of the ν₄ (NH₄+) mode decreases which can be associated with the order parameter and its FWHM increases as the temperature increases toward the transition temperature Tc from low temperature (ordered phase) for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ as observed experimentally [5], so that the temperature dependence of the IR frequency and FWHM of this mode can be calculated for those compounds. The anomalous behaviour of the observed IR frequency and FWHM of the ν₄ (NH₄+) mode can then be explained for the order-disorder transition in NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ compounds on the basis of the calculations by using the models used in this study. This is the motivation of our study given here to investigate the mechanism of the phase transitions in the MOFs considered. For the IR frequency of the ν₄ (NH₄+) mode, we use the molecular field theory [11] by calculating the temperature dependence of the order parameter. For the FWHM of this mode, we use mainly pseudospin-phonon coupling (PS) model [12] and also energyfluctuation (EF) model [13] for the damping constant of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃.

Materials and Methods

Temperature-dependent raman spectra were obtained for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, which were measured using a bruker FT100/S spectrometer with YAG:Nd laser excitation (1064 nm) and a helium-flow oxford crysostat as pointed out in the previous study [5]. The vibrational spectra of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ were regarded as composed of internal vibrations of the ammonium and formate ions, and the lattice vibrations, in particular, the bending modes ν₂ and ν₄ of the ammonium cation were observed [5] near 1600-1720 and 1390-1460 cm^-1 (1100-1300 and 1050-1150 cm^-1) for NH₄+(ND₄+), respectively [14-16].

The temperature dependent changes in vibrational spectra, in particular, plots of frequencies and full width at the half-maximum (fwhm) values for a number of structural units were presented [5]. In the present study, temperature dependence of the bending modes of ν₄ (1440 cm^-1) NH₄ and ν₄ (1084 cm^-1)ND₄+ are given (Figure 1). Temperature-dependent Raman spectra [5] are analyzed to predict the frequencies and FWHM for the bending modes ν₄ NH₄+ and ν₄ ND₄+ of NH₄Zn(HCOO)₃and ND₄Zn(DCOO)₃, respectively in this study.

Calculations and Results

The order parameter S can be calculated below the transition temperature T_c by the molecular field theory [11] according to the relation

Regarding order–disorder transition in molecular crystals, the critical behaviour of the frequency can be associated with the order parameter close to the transition. In particular, ν₄ (NH₄+) infrared mode frequency is the driving mechanism of the order-disorder transition in the metal formate frameworks (MOFs) of the compounds NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃. The temperature dependence of this IR mode can be considered as an order parameter in those MOFs. On that basis, we have related the IR frequency of the ν₄ (NH₄+) mode to the order parameter by considering the temperature dependence of the frequency as

according to the relation

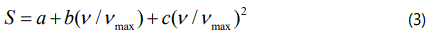
where a₀, a₁, a₂, a, b and c are all constants. ν_max denotes the maximum value of the IR ν₄ (NH₄+) frequency to normalize it (ν/ν_max) since the order parameter (S) varies from 0 to 1. We assume here quadratic dependence of the order parameter on the frequency (Eq.3).

We first analyzed the temperature dependence of the ν₄(NH₄+) IR mode frequencies by using the experimental data [5] according to Eq.(2) with the parameters a₀, a₁ and a₂ determined (Table 1). Calculated order parameter S (Eq.1) was then fitted to the observed frequency data (ν/νmax) by using Eq. (3) with the parameters a, b and c below T_c (Table 1). This analysis and calculation of the IR ν₄(NH₄+) mode were performed for the NH₄Zn(HCOO)₃ and its deutero compound of ND₄Zn(DCOO)₃ with the IR frequencies of 1440 and 1084 cm^-1, respectively. Above T_c, since S=0 (Eq.1) the observed IR frequency data [5] were analyzed by using Eq.(2) with the parameters a₀, a₁ and a₂ within the temperature intervals considered, as given in table 2. Figures 2 and 3 give the calculated wave numbers of 1440 and 1084 cm^-1 for the ν₄(NH₄+) IR mode, with the observed data [5] as a function of temperature for the compounds of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ respectively.

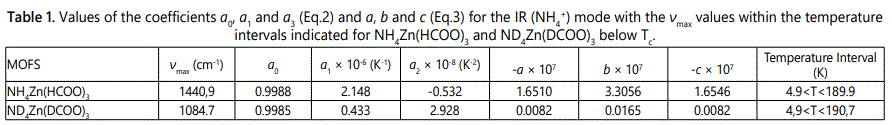
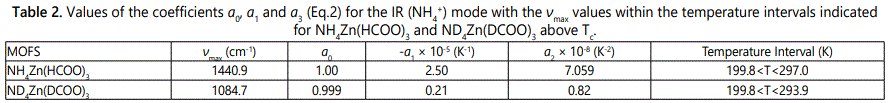
Temperature dependence of the damping constant (FWHM) can also be evaluated by using the ν₄ (NH₄+) IR mode frequency as an order parameter for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃. For this calculation, the pseudospin-phonon coupled (PS) model [12] was employed according to the relation

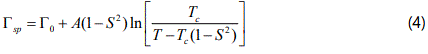
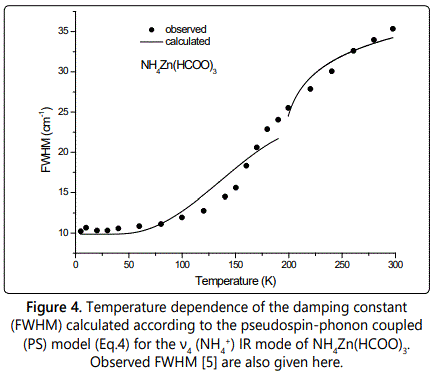
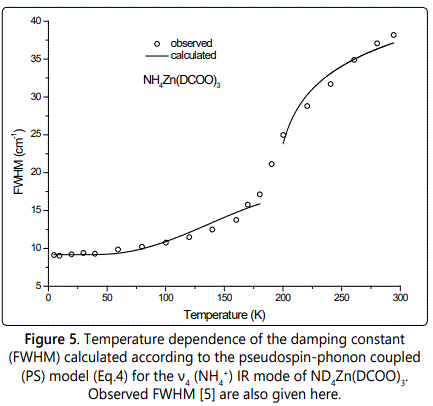
where Γ₀ represents the background damping constant Γ_SP due to the coupling between pseudospin (PS) of the (NH₄+) ions and phonon in those MOFs and A is the amplitude. In Eq.(4) we used the IR ν₄ (NH₄+) frequency as an order parameter S. This calculation of Γ_SP was carried out below (S≠0) and above (S=0) the transition temperature TC. Figures 4 and 5 give our calculated FWHM (damping constant Γ_SP) according to Eq.(4) by using the 1440 and 1084 cm^-1 IR frequencies calculated (Eqs.1 and 3) of the ν₄ (NH₄+) IR mode for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ compounds, respectively, with the observed FWHM of those modes [5]. Table 3 gives the values of Γ₀ and A for both IR modes (1440 and 1084 cm^-1).

Discussion

The IR frequency of the ν₄ (NH₄+) mode for the MOFs of NH₄Zn(HCOO)₃ (1440 cm^-1) and ND₄Zn(DCOO)₃ (1084 cm^-1) was calculated as an order parameter S from the molecular field theory (Eq.1) through Eqs.(2) and (3) at various temperatures (Figures 2 and 3) as stated above. Our fits are reasonably good indicating that the ν₄ (NH₄+) IR mode can be considered as an order parameter and it can be associated with the mechanism of the order-disorder transition in those MOFs. In a wide temperature range below the transition temperature (T_C≈191 K), we find that the molecular field theory (Eq.1) describes adequately the observed behaviour of the ν₄ (NH₄+) IR mode frequency. Close to T_C, the temperature dependence of the order parameter S is given by the relation from the molecular field theory [11],

with the critical exponent β=1/2 for the order parameter according to the power-law S ∝∈^β where the reduced temperature is ∈=(T_c-T)/T_c. Thus, in the vicinity of T_C, the ν₄(NH₄+) IR frequency data can be analyzed by the power-law formula and the β-value (different from 1/2) can be obtained for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃. This requires the IR frequencies measured accurately in a very narrow temperature interval around T_C.

For the mechanism of the phase transition in NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, the effect of isotopic substitution can be investigated since it influences phase transition temperature and facilitates assignment of modes to the respective motions of atoms in the unit cell [5] in these compounds with the extensive H-bonds. It has been pointed out that temperature-dependent studies reveal a very weak isotopic effect on the phase transition temperature and that ordering of ammonium cations plays a major role in the mechanism of the phase transition [5]. In fact, for both compounds of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, transition temperature is almost the same (≈191 K) and due to the reorientations of the NH₄+(ND₄+) ions the ordered phase occurs at low temperatures (below T_C). This also explains the multiferroic behaviour of those compounds at low temperatures.

Regarding the temperature dependence of the damping constant Γ_SP (FWHM) due to the pseudospin-phonon coupling for the ν₄ (NH₄+) IR mode, the pseudospin-phonon coupled (PS) model is satisfactory to describe the observed behaviour of the IR line widths of this mode below T_C (Figures 4 and 5). Above T_C, since the order parameter is zero (S=0) as predicted from the molecular field theory (Eq.1) without using any IR frequency, Eq.(4) was fitted to the observed FWHM data of this mode, as mentioned before. We also used the energy fluctuation (EF) model [13] according to the relation

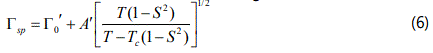
where Γ₀^′ and A^′ are the background bandwidth and amplitude, respectively, as before. In contrast to the PS model, when Eq.(6) was fitted to the ν₄ (NH₄+) mode for the MOFs of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ it was found that the agreement was not satisfactory. Most likely, this is due to the fact that the damping constant varies with the temperature as Γ_SP∝(T-T_c)^-1/2 with the critical exponent value of 1/2 (for example, when S=0 above T_C). This then indicates that the EF model (Eq.6) can describe the observed behaviour (FWHM) in the vicinity of the T_C (in a very narrow temperature range) for the ν₄ (NH₄+) IR mode of those MOFs. We note that for both models (PS and EF) due to the reorientation of the NH₄+ ions which are ordered below T_C, interaction between ammonium cations (spin) and the displacement of the metal formate framework (phonon) is considered for the mechanism of phase transitions in NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃.

Increase in FWHM (Figures 4 and 5) indicates that the phase transition in NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃ has an order-disorder character and it is associated with the rotational dynamics of the ammonium cations [3,4] as also pointed out previously [5]. Including phonon-phonon anharmonic interactions, from the temperature dependence of FWHM of the ν₄ (NH₄+) modes the activation energy was calculated in the thermal activated reorientational processes as 86 and 93 meV for NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃, respectively [5]. This shows that if the potential curve for the motion of ND₄+ equals that of NH₄+, the activation energy for the reorientation increases by the deutration due to the increase of the moment of inertia [17], as also pointed out previously [5]. This is also an indication of the interaction between the ammonium cations and anionic framework, which is weakly affected by the deuteration [5].

Conclusions

The infrared (IR) frequencies and the line width (damping constant) of the ν₄ (NH₄+) mode were calculated as a function of temperature close to the order-disorder transition in the MOFs of NH₄Zn(HCOO)₃ and ND₄Zn(DCOO)₃. The IR frequency of this mode as an order parameter and its damping constant (FWHM) were calculated from the molecular field theory and the pseudospin-phonon coupling (PS) model, respectively.

Our results show that the observed behaviour of the IR frequency and the line width for the ν₄ (NH₄+) mode can be described satisfactory by the models used for the compounds studied here.

References

1. Wang Z, Zhang B, Inoue K, et al. Occurrence of a Rare 4⁹ ·6⁶ Structural Topology, Chirality, and Weak Ferromagnetism in the [NH₄][MII(HCOO)₃] (M=Mn, Co, Ni) Frameworks. Inorg Chem. 2007; 46(2): 437-445. doi: 10.1021/ic0610031   
2. Xu GC, Zhang W, Ma XM, et al. Coexistence of Magnetic and Electric Orderings in the Metal–Formate Frameworks of [NH₄][M(HCOO)₃]. J Am Chem Soc. 2011; 133(38): 14948-14951. doi: 10.1021/ja206891q   
3. Mączka M, Pietraszko A, Macalik B, Hermanowicz K. Structure, Phonon Properties, and Order–Disorder Transition in the Metal Formate Framework of [NH₄][Mg(HCOO)₃]. Inorg Chem. 2014; 53(2): 787-794. doi: 10.1021/ic4020702   
4. Zhang R, Xu GC, Wang ZM, Gao S. Phase transitions, prominent dielectric anomalies, and negative thermal expansion in three high thermally stable ammonium magnesium-formate frameworks. Chemistry. 2014; 20(4): 1146-1158. doi: 10.1002/chem.201303425   
5. Mączka M, Kadłubański P, Freire PTC, et al. Temperature- and PressureInduced Phase Transitions in the Metal Formate Framework of [ND₄][Zn(DCOO)₃] and [NH₄][Zn(HCOO)₃]. Inorg Chem. 2014; 53(18): 9615-9624. doi: 10.1021/ic501074x   
6. Nibbering ETJ, Dreyer J, Kühn O, Bredenbeck J, Hamm P, Elsaesser T. Vibrational dynamics of hydrogen bonds. In: Kühn O, Wöste L (eds). Analysis and Control of Ultrafast Photoinduced Reactions. Chemical Physics. 2007; 87: 619-687.   
7. Sobczyk L, Obrzyd M, Filarowski A. H/D Isotope Effects in Hydrogen Bonded Systems. Molecules. 2013; 18(4): 4467-4476. doi: 10.3390/molecules18044467   
8. Carabatos-Nédelec C, Becker P. Order–disorder and structural phase transitions in solid-state materials by Raman scattering analysis. J Raman Spectrosc. 1997; 28: 663-671. doi: 10.1002/(SICI)1097-4555(199709)28:9<663::AID-JRS157>3.0.CO;2-L   
9. Cummins HZ, Levanyuk AP. Light Scattering Near Phase Transitions. North-Holland Publishing Company. 1983: 682.   
10. Guo M, Cai HL, Xiong RG. Ferroelectric metal organic framework (MOF) Inorg Chem Commun. 2010; 13(12): 1590-1598. doi: 10.1016/j.inoche.2010.09.005   
11. Brout R. Phase Transitions. Chapter 2. Benjamin WA Publisher. New York, USA. 1965.   
12. Lahajnar G, Blinc R, Zumer S. Proton spin-lattice relaxation by critical polarization fluctuations in KH₂PO₄. Phys Cond Matte . 1974; 18(4): 301-316.   
13. Schaack G, Winterfeldt V. Temperature behaviour of optical phonons near Tc in triglycine sulphate and triglycine selenate. Ferroelectrics. 1977; 15(1): 35-41. doi: 10.1080/00150197708236718   
14. Hadrich A, Lautié A, Mhiri T. Vibrational study of structural phase transitions in (NH₄)₂HPO₄ and (ND₄)₂DPO₄. J Raman Spectrosc. 2000; 31(7): 587-593. doi: 10.1002/1097-4555(200007)31:7<587::AID-JRS581>3.0.CO;2-7   
15. Kruger A, Heyns AM. A Raman and infrared study of (NH₄)₂ZrF₆. Vib Spectrosc. 1997; 14(2): 171-181. doi: 10.1016/S0924-2031(96)00072-0   
16. Fredrickson RL, Decius JC. The Raman spectrum of the ordered phase of NH₄Cl and ND₄Cl: Dipole and polarizability derivatives. J Chem Phys. 1977; 66: 2297. doi: 10.1063/1.434291   
17. Asaji T, Ishizaka T. Effect of Deuteration on Ammonium Motion and Structural Phase Transition Studied by Nuclear Quadrupole Resonance. Z Naturforsch. 2000; 55: 83-89.