Abstract

The present article is aimed at an investigation of the propagation of elasto-thermodiffusive (ETN) surface waves in a homogenous isotropic, thermally conducting, semiconductor material half-space underlying a thermally conductive viscous or inviscid liquid layer of finite thickness (d) with varying temperature. The relaxation times of heat and charge carrier fields are also taken into consideration during the study. Secular equation that governs the propagation of elasto-thermodiffusive surface (interfacial) waves in the considered composite structures has been derived in compact form after obtaining general wave solution of the model. Some particular forms of the general secular equation are also deduced and investigated. Numerical solution of secular equation and other relevant relations is carried out for germanium (Ge) and silicon (Si) semiconductor material under different situations with the help of functional iteration numerical technique along with irreducible case of Cardanoʼs method.

Keywords: Thermal Relaxation time; Rayleigh wave; Diffusion; Lifetime; Thermally conductive liquid; Semiconductor.

Background and Introduction

Surface acoustic waves are one of the broad classes of acoustic waves used in ultrasonic applications. These are also applied to the study of physical changes at the solid-liquid interfaces of materials in contact with fluid. The generation of acoustic (or elastic) waves due to the transient thermal heating of a material is rapidly becoming a powerful tool for characterization of the material impinging on its microstructure. The surface acoustic waves are also widely used in electronics and medical devices because of the following reasons:

(i) The propagation velocities of these waves are of the order of a few km/sec leading to the much smaller dimensions of the devices;

(ii) The energy of these waves is concentrated in the vicinity of the top of the surface of the device, so that generation, detection and control are directly possible and can be done on the surface itself.

The theories of elastic and thermoelastic wave propagation are well established by Graff [1] and Nowacki [2]. Maruszewski [3-7] presented theoretical considerations of the simultaneous interaction between elastic, thermal and charge carrierʼs fields in semiconductors. Sharma and Thakur [8] studied the plane harmonic elastothermodiffusive (ETNP) waves in semiconductor materials. The shear waves get decoupled from rest of the motion and remain independent of the influence of other fields. According to the frequency equation, four coupled longitudinal waves namely; quasi-thermoelastic (QTN), elastodiffusive (QEN/QEP), thermodiffusive (QTN/QTP), and a quasi-thermal (T-mode); are possible to be propagated in an infinite semiconductor. Sharma et al. [9-10] investigated the propagation characteristics of elasto-thermodiffusive (ETN) surface acoustic waves in a semiconductor material half-space. The effects of thermal relaxation and life times of charge carrier fields on the various characteristics of elasto-thermodiffusive (ETN) surface waves propagating in a semiconductor material have been investigated. Sharma et al. [11] investigated the propagation of elasto-thermodiffusive surface wave in a semiconductor half-space underlying a fluid with varying temperature. Sharma et al. [12] studied acoustodiffusive Rayleigh waves in a semiconductor material half space in contact with fluid medium. Sharma et al. [13] studied the acousto thermodiffusive interfacial waves in a semiconductor loaded with viscous fluid. Sharma et al. [14] studied the reflection of acoustodiffusive waves from the boundary of a semiconductor half space. Sharma et al. [15] investigated the modeling of reflection and transmission of acoustic waves at fluid semiconductor interface. Sharma [16] investigated the effect of liquid loading on lamb waves in a semiconductor material plate.

Initial work relating to the use of acoustic wave devices in liquid-phase sensing applications utilized conventional bulkacoustic-wave (BAW) piezoelectric crystal resonators investigated by Kansh and Bartiaans [17]. Josse et al. [18] presented an analytical solution for the resonance condition of the piezoelectric quartz resonator with one surface in contact with viscous conductive liquid.

The present paper is aimed at an investigation of the propagation of elasto-thermodiffusive (ETN) surface waves in a homogenous isotropic, thermally conducting, semiconductor material half-space underlying a thermally conductive viscous or inviscid fluid layer of finite thickness (d) with varying temperature. It is based on the model of governing equations derived by Maruszewski [6] and non-dimensionalized by Sharma and Thakur [8]. The relaxation times of heat and charge carriers are also taken into consideration during the study. Secular equation that governs the propagation of elastothermodiffusive surface (interfacial) waves in the considered composite structure has been derived in compact form after obtaining general wave solution of the model. Some particular forms of the general secular equation are also deduced and investigated. Numerical solution of secular equation and other relevant relations is carried out for germanium (Ge) and (Si) semiconductor material under different situations with the help of functional iteration numerical technique along with irreducible case of Cardanoʼs method. The computer simulated results have been presented graphically.

Formulation of the problem

Consider an extrinsic, homogeneous, isotropic, thermally conducting, elastic n-type semiconductor half-space, initially under undeformed state at uniform temperature T₀. The semiconductor is loaded with fluid layer of finite thickness d. The considered fluid may be inviscid or viscous with varying temperature but thermally conducting which can be modeled as a heat source in addition to normal hydrostatic load. The surface of the semiconductor is assumed to be in welded contact with the fluid medium. We take the origin of rectangular Cartesian coordinate system oxyz on the interface surface of both media and z-axis pointing normally into the semiconductor half-space, which is thus represented by z ≥ 0. The x-axis is taken along the direction of acoustic wave propagation in the semiconductor half-space. Here, we focus of the same geometry as given in Figure 1. All particles on a line parallel to y-axis are assumed to be equally displaced so that all field quantities remain independent of y-coordinate viz ∂/∂y ≡ 0. Further the disturbance is assumed to be confined to the neighbourhood of the free surface and hence vanishes as z→∞.

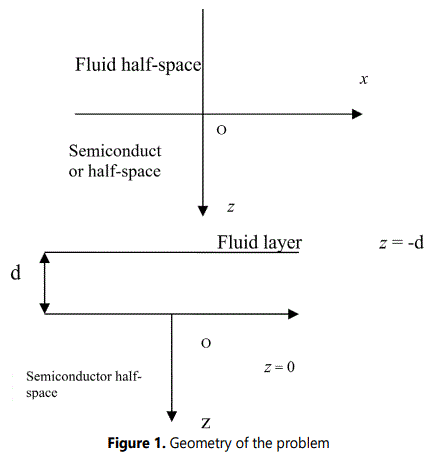
In linear theory of thermoelasticity for semiconductors, the non-dimensional governing field equations for temperature change T(x, z, t), displacement vector u(x, z, t) = (u, 0, w) and electron diffusion field N(x, z, t); in the absence of body forces, electro-magnetic forces and heat sources; are given by Maruszewski [6] and Sharma and Thakur [8].

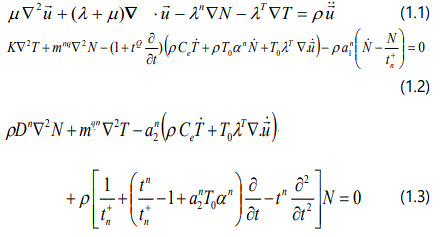
where we have used the notations

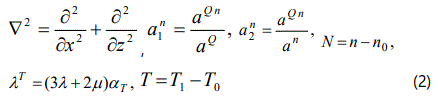
Here λ , μ are Lame parameters ; ρ is the density of the semiconductor; λⁿ are the elasto-diffusive constants of electrons, α_T is the coefficient of linear thermal expansion of the material; K is the thermal conductivity, αⁿ is the thermo-diffusive constant of electrons; a^Qn, a^Q, aⁿ are flux like constants; Dⁿ is the diffusion coefficient of electron. The quantities m^nq and m^qn are the Peltier-Seebeck-Dufour-Soret like constants; t^Q, tⁿ are respectively, the relaxation times of heat and electron fields, C_e is the specific heat at constant strain, t_n⁺ denotes the life time of the carriersʼ field and n₀ is the non-equilibrium concentration of electron. The densities of the charge carriers at doping level are assumed to be of such values that the life time , t_n⁺ and the diffusion coefficient Dⁿ is independent of them.

Further the equations (1) are subjected to the following assumptions:

(i) All the considerations are made in the frame work of the phenomenological model.

(ii) The electric neutrality of the semiconductor is satisfied.

(iii) The magnetic field effect is ignored.

(iv) The mass of charge carrier fields is negligible.

(v) The electron field within the boundary layer is very weak and can be neglected.

(vi) The recombination function of electrons is reduced on the basis of the facts that take care of defects and hence concentration values of the charge carrier field [19].

We define the quantities

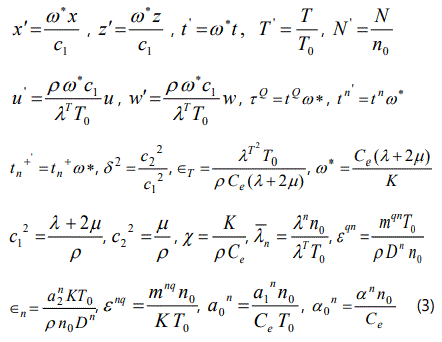
where ω^∗ and ε_T are respectively, the characteristic frequency and thermoelastic coupling parameters of the semiconductor.

Upon introducing the quantities (3) in the basic equations (1), we obtain

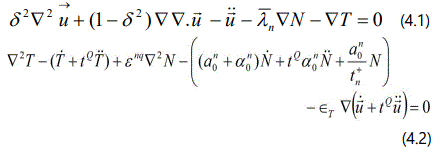
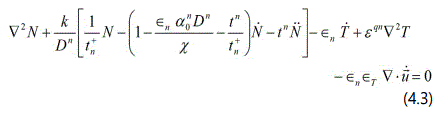
We introduce the scalar point potential function φ and vector point potential function ψ = (0, −ψ , 0) through the relations

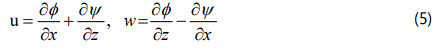
The substitution of expressions (5) in equations (4) leads to

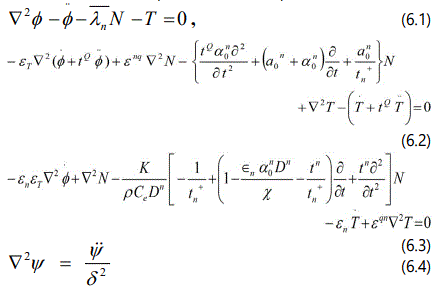
The equation (6.4) corresponds to purely transverse waves which get decoupled from rest of the motion and are not affected by the thermal and charge carrier fields. This elastic wave travels in space without attenuation. The equations (6.1) to (6.3) in the above system can be simplified under the assumption that is considered semiconductor of relaxation type. For such materials, the diffusion approximation of the physical process ceases to be obligatory and the diffusion / life times (tⁿ/t_n⁺) become comparable to each other in their values (tⁿ = t_n⁺).

In liquid medium the velocity components are given by

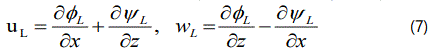
where φ_L and ψ_L are respectively, the scalar and vector point velocity potentials. Thus in the liquid medium the governing equations are given by

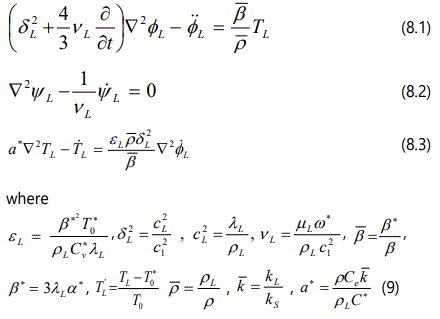
Here, c_L is the velocity of sound in liquid, λ_L is the bulk modulus, ρ_L and μ_L is respectively the density and dynamic viscosity of the liquid; α^* is the coefficient of volume thermal expansion; and T_L is the temperature deviation of liquid medium from ambient temperature T₀^∗. In case of non-conducting liquid (k = 0) , so that a^* = 0 the equation (8.3) becomes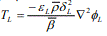

Boundary conditions

The continuity of stresses, displacement, electron concentration, temperature change, electron and heat fluxes on the solid-fluid interface is assumed to be satisfied. This leads to the following non-dimensional boundary conditions at the solid-fluid interface (z =0) .

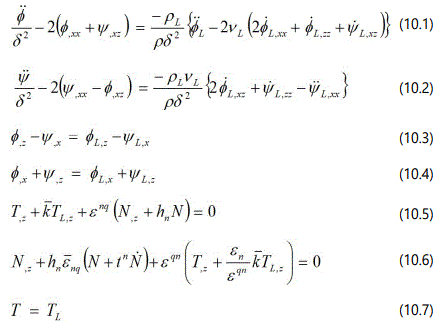
In case of non-conducting fluid (k = 0) the boundary conditions (10.5) to (10.7) reduces to

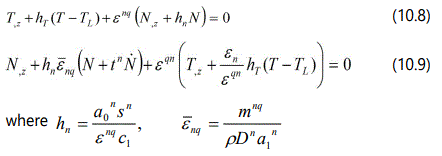
Here h_n → 0 correspond to thermally insulated and charge free (no flow of electron flux across the boundary) boundary and h_n → ∞ refers to isothermal and equipotential one.

Formal solution

We consider the case of time harmonic waves so that the solutions φ, T, N, and ψ , φ_L , ψ_L of equations (6) take the form:

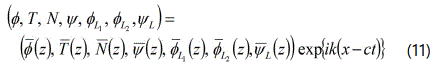
where c = ω/k, is the phase velocity, k and ω are respectively the wave number and angular frequency of the waves. Upon using solutions (11) in equations (6), after lengthy but straight forward algebraic reductions and simplifications, we obtain the following formal solution for (φ N T ψ φ_L1 φ_L2 ψ_L) that satisfies the radiation conditions R_e (m_i) ≥ 0 and R_e (γ_i) ≤ 0 i = 1, 2, 3, 4 , we have

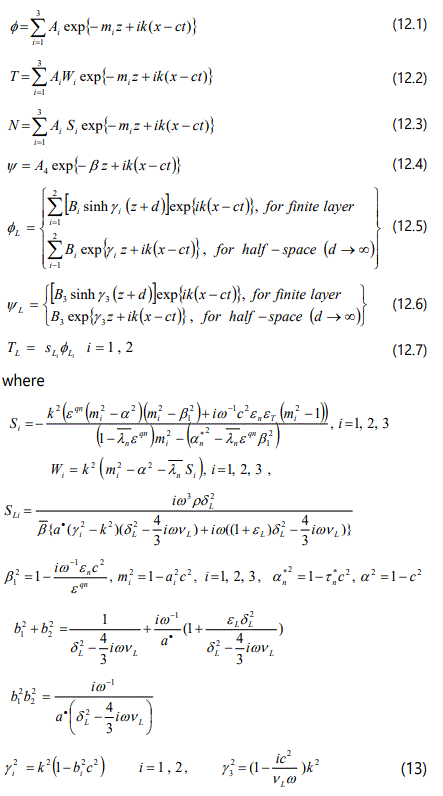
Here a_i², i= 1,2,3 are the roots of the complex cubic equation

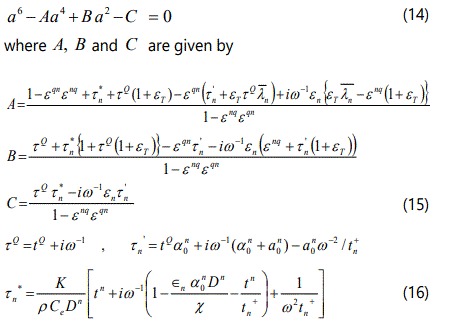
In case of relaxation type semiconductor life time and relaxation time are comparable (tⁿ = tⁿ⁺) and consequently τ_n^* gets modified. In general, the characteristic roots m_i (i = 1, 2, 3) are complex and as we are considering surface waves only, so without loss of generality we choose only that form of m_i and γ_i which satisfies the radiation condition required for the boundedness of the solution. Hence the solution is a superposition of the plane waves attenuating with depth.

Derivation of dispersion relation and its reductions

We consider the situation in which semiconductor half-space is in contact (or loaded) with viscous inviscid liquid. Upon applying the required interface boundary conditions (10) at the solid-fluid interface (z = 0) and subsequently requiring non-trivial solution of the resulting coupled equations, after lengthy but straight forward algebraic reductions and simplifications, the secular dispersion relation for Rayleigh surface waves is obtained as

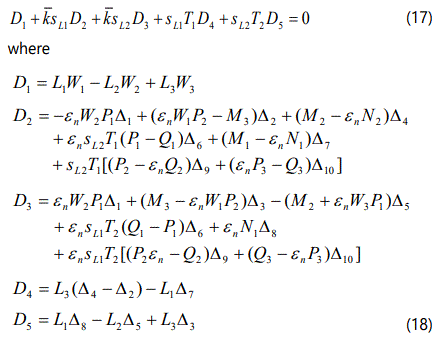
Here L₂, L₃ can be obtained from L1 by replacing the subscripts permutation (2, 3) with (1, 3), (1, 2), respectively. The secular equation (17) governs the motion of modified guided elasto-thermodiffusive (ETN) Rayleigh (Stoneley) waves in the instant analysis. It contains complete information about the phase velocity, attenuation coefficient and other characteristics of the ETN surface waves in a thermoelastic semiconductor half-space loaded with liquid layer of finite thickness with varying temperature.

In case of non-conducting fluid k->0 => a^*->0, so that

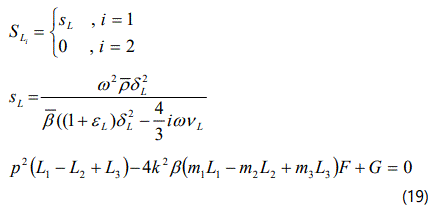
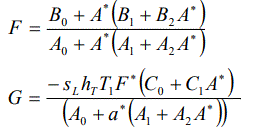
Solution of secular equation

The characteristic roots m_i,γ_i (i= 1,2,3) given by equation (14) are in general complex and therefore, the wave number and hence, phase velocities of the waves are complex quantities. Therefore, the waves are attenuated in space.

If we write

so that k = R + iQ, R = ω/ V where V and Q are real. The exponent in the plane wave solution (11) becomes iR (x −V t)−Q x, which shows that V is the propagation speed and Q the attenuation coefficient of the waves. Upon using equation (20) in secular equation (17) and other relevant relations, the values of phase speed (V) and attenuation coefficient (Q) for the propagation of Rayleigh waves can be obtained for different values of the wave number (R) . The secular equations (17) and (19) being algebraic equations in the case of leaky waves and transcendental equations for non-leaky are of the form f (m, R, V, Q) = 0 . For known values of m these equations can be solved to compute phase velocity (V) and attenuation coefficient (Q) for fixed values of wave number (R) and given V = V₀ , Q = Q₀. We shall use functional iteration method to solve the secular equations for phase velocity (V) and attenuation coefficient (Q) for different values of wave number (R) and procedure adopted is outlined below.

The functional iteration method to solve of an equation of the form g(V) = 0, requires to put this equation in the form V = F(V), so that the sequence {Vn } of iterations for the desired root can be easily generated as follows. If V = V₀ be the initial approximation to the root, then we have V₁ = F (V₀)V₂ = F(V₁), V₃ = F(V₂),... and so on. In general, V_n+1 = F(V_n), n=0,1,2,3. If |F(V)<<1, for all V ∈ I , then the sequence {V_n} of approximations to the root will converge to the actual value V = V_a of the root, provided V₀ ∈ I. Here I is the interval in which roots is expected. For initial values of V = V₀ and Q = Q₀, the values of m_i , γ₁ (i = 1,2,3) can be obtained from equation (13) and then these values are further used in secular equations (17) and (19) to obtain current values of V and Q which are then used to generate a new approximation until or unless the sequence of iterations to the values of V or Q converges to the desired level of accuracy. That is the condition |V_n+1 - V_n| <∈, ∈being arbitrarily small number to be selected at random in order to achieve the accuracy level, is required to be satisfied. This process is continuously repeated for different values of wave number (R) to obtain phase velocity (V) and attenuation coefficient Q. Consequently, the specific loss of energy (SL) and relative frequency shifts (RFS) can also be computed. The specific loss is the rate of energy dissipation |∆W/W| in a stress cycle of the specimen when the strain is maximal. It is given by |∆W/W| = 4π(Im(k)/Re(k))), k being complex. Here, we have κ = |∆W/W| = 4π(VQ/ω)

Numerical results and discussions

In this section, we present some numerical results in order to illustrate the analytical developments carried out in the previous sections. To understand the interactions of various fields in thermoelastic semiconductors, the non-dimensional phase velocity (V), attenuation coefficient(Q) and specific loss factor of energy dissipations (κ) of ETN-surface wave modes under different situation have been obtained and computed numerically for semiconductor half-space loaded with thermally conductive liquid. The secular equations (17) and (19) have been solved numerically by using fixed point iteration technique. The materials chosen for this purpose is Germanium (Ge) and Silicon (Si), the physical data for which is given in Tables 1. The fluid loading is considered to be ideal water (H₂O) and heavy water (D₂O) for the purpose of numerical computations whose physical data is given in Tables 2, 3

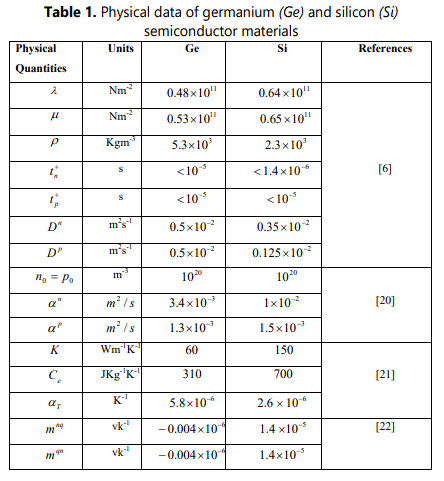
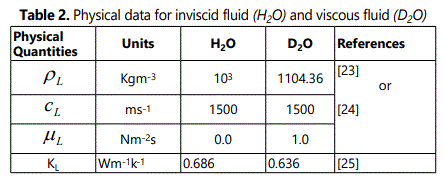
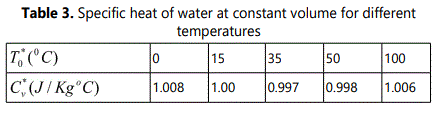
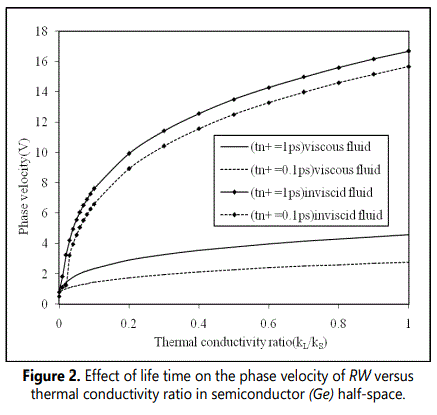
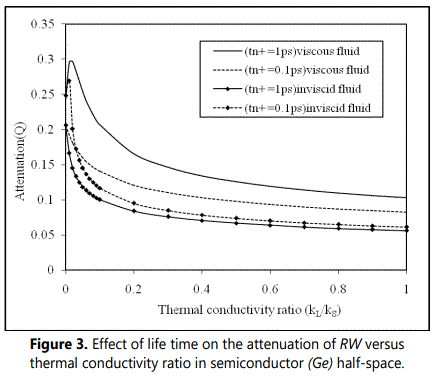
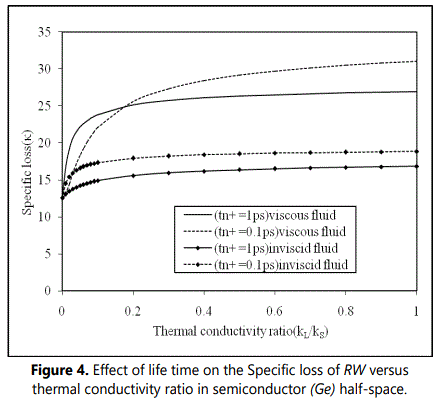
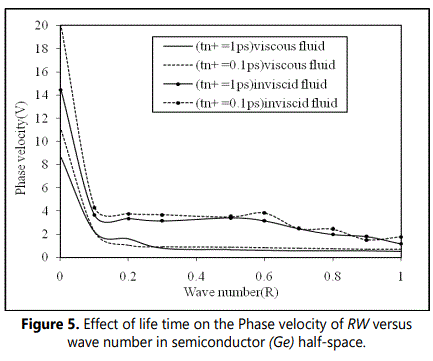
Figure 2 shows the variation of phase velocity with thermal conductivity ratio (k‾) at life time t_n⁺ = 1ps and 0.1ps when germanium (Ge) semiconductor half-space is loaded with thermal conductive viscous or inviscid liquid. It is observed that considerable changes that occur in phase velocity are for relatively narrow interval of thermal conductivity ratio 0 ≤ (k‾)≤1. It is found that the magnitude of phase velocity (V) increases uniformly with thermal conductivity ratio (k‾) . The behaviour of dispersion curves for generalized Rayleigh Stoneley waves, in both viscous / inviscid liquid loadings is found to be similar except that the magnitude of phase velocity of latter is quite large as compared to that of former one. It is also observed that the magnitude of the phase velocity increases with increasing life time of charge carrier field in case of both inviscid and viscous liquid loadings. Figure.3 shows the variations of attenuation coefficient (Q) with thermal conductivity ratio (k‾) for life times t_n⁺ = 1ps and 0.1ps when semiconductor is loaded with thermally conducting viscous or inviscid liquid. It is noticed that for both viscous and inviscid liquid, the attenuation decreases exponentially with thermal conductivity ratio (k‾). The magnitude of attenuation is found to be higher in case of viscous liquid than that for inviscid liquid loading. Figure 4 shows the variations of specific loss factor of energy dissipation (κ) with thermal conductivity ratio (k‾) at life times t_n⁺ = 1ps and 0.1ps. From Figure. 4, it is observed that the specific loss factor increases monotonically with thermal conductivity ratio (k‾) up to 0.2 thereafter it become constant. However, the magnitude of specific loss factor of energy dissipation (κ) for viscous liquid is found to be quite large than that in case of inviscid liquid loading. Figure 5 shows the variations of phase velocity of surface waves with wave number (R) at different life times in the case of inviscid or viscous liquid loadings. The considerable changes of phase velocity are noticed to occur within relatively narrow interval of wavenumber (R) . It is found that the magnitude of phase velocity (V) decreases in the wave number range 0 ≤ R ≤ 0.2 before it becomes steady and uniform for R ≥ 0.2 , at life times t_n⁺ = 1ps and 0.1ps.

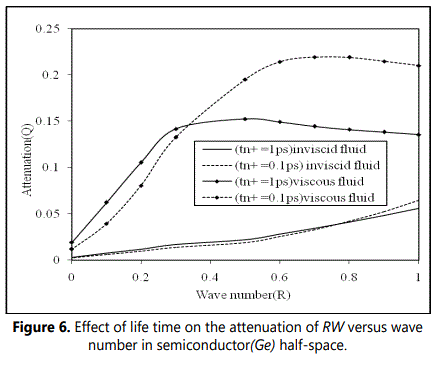
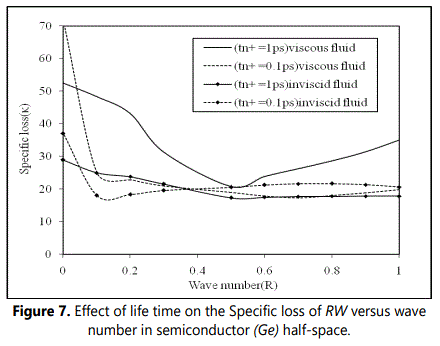
Figure 6 shows the variation of attenuation coefficient (Q) of generalized Rayleigh waves with wave number for different life times of semiconductor loaded with thermally conducting. It is revealed that the attenuation coefficient (Q) increases linearly for wave number interval 0 ≤ R ≤ 0.4 and after R ≥ 0.4 it becomes constant in case of viscous liquid loading. It is noticed that for inviscid liquid loading, the attenuation first increases in the range and then decreases monotonically for . The magnitude of attenuation coefficient (Q) in case of viscous liquid is found to be quite large as compared to inviscid fluid loading. This is attributed to the fact that when a wave travel along the interface, the fluid in immediate contact with the solid is at rest and subsequent layers of fluid may have a velocity that increases with increasing depth from the solid surface. The velocity gradient causes an internal stress associated with viscosity that leads to loss of momentum and this loss of momentum results in decrease of amplitude (attenuation) of the wave close to the surface. Figure 7 shows the variations of specific loss factor of energy dissipation (κ) with wave number (R) at life times t_n⁺ = 1ps and 0.1ps. The Figure. 7 revealed that the specific loss factor of considered waves first decreases in the interval and then increases monotonically with increasing wave number for , at all considered values of life times.

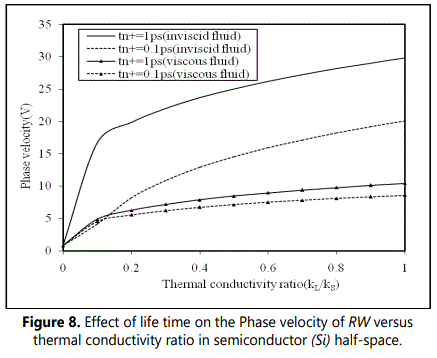
Figure 8 presents the variation of phase velocity with thermal conductivity ratio (k‾) at life times t_n⁺ = 1ps and 0.1ps in a silicon (Si) semiconductor loaded with thermally conducting viscous or inviscid, liquid.

It is noticed that the considerable changes of phase velocity that occur are within relatively narrow interval of thermal conductivity ratio 0 ≤ (k‾)≤1. It is found that the magnitude of phase velocity (V) for thermally conducting fluids both inviscid and viscous increases uniformly with thermal conductivity ratio (k‾). The behaviour of dispersion curves of generalized Rayleigh waves in case of both viscous and inviscid liquid loadings is found to be similar except that the magnitude of phase velocity in latter case is quite large as compared to that former one. It is also observed that the magnitude of the phase velocity is found to increase with increase in life time of charge carrier fields for both inviscid and viscous liquid loadings.

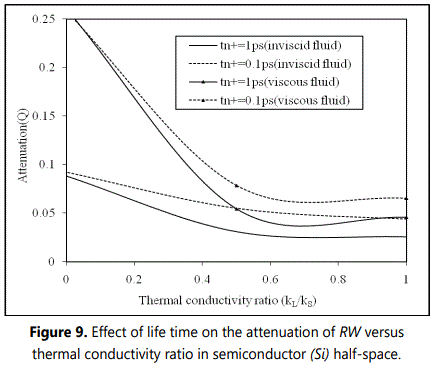
Figure 9 shows the variation of attenuation coefficient (Q) with thermal conductivity ratio (k‾) at life times t_n⁺ = 1ps and 0.1ps in silicon (Si) semiconductor half-space loaded with thermally conducting viscous or inviscid liquid. It is noticed that the attenuation decreases exponentially with thermal conductivity ratio (k‾) for both viscous and inviscid liquid loadings. The magnitude of attenuation in case of viscous liquid is found to be quite large as compared to that of inviscid liquid loading.

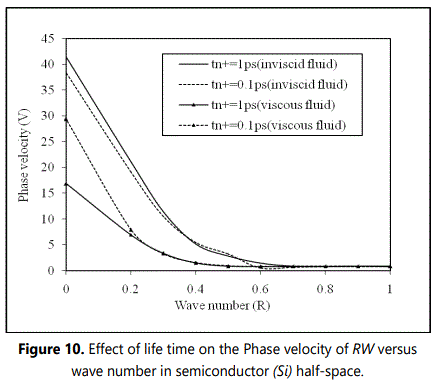
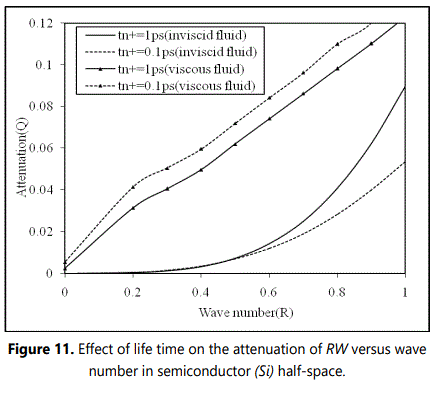
Figure 10 shows the variations of phase velocity of generalized Rayleigh waves with wave number (R) at different life times in the case of inviscid or viscous liquid loading. Considerable changes of phase velocity that occur have been observed within relatively narrow interval of wave number (R) . It is found that the magnitude of phase velocity (V) decreases in the wave number range 0 ≤ R ≤ 0.2 before it becomes steady and uniform R ≥ 0.2 , at life time t_n⁺ = 1ps and 0.1ps in a silicon (Si) semiconductor half-space is loaded with thermally conducting viscous and inviscid liquid. Figure 11 represents the variation of attenuation coefficient (Q) of considered waves with wave number at different life times in silicon (Si) semiconductor loaded with liquids. From Figure 11, it is observed that in case of viscous liquid loading, the attenuation coefficient (Q) increases linearly with wave number. It is noticed that for inviscid liquid loading, the attenuation first increases linearly for and then increases monotonically in the wave number range . It is also formed that the magnitude of attenuation coefficient (Q) in case of viscous liquid loading is found to be quite large than inviscid.

Conclusions

In this paper we have introduced the effect of thermally conducting fluid, both inviscid and viscous, loadings on the characteristics of generalized Rayleigh waves in a n-type semiconductor propagating along solid-liquid interface. It is found that the fluid layer in contact with semiconductor causes significant changes in phase velocity, attenuation and specific loss of generalized Rayleigh waves. The behaviour of dispersion curves for both types of liquid loadings is found to be of similar nature expect that the magnitudes of phase velocity, attenuation and specific loss for inviscid liquid loading is quite larger than their counterparts in case of viscous one. This may be due to adhesive forces at solidliquid interface and liquid density, the energy dissipation is more in viscous liquid as compared to inviscid liquid loading. The attenuation caused by liquid loading is attributed to the combined effects of radiation losses due to energy leakage into the liquid and dissipative losses because of viscous friction at the interface. It may be contribution of its dependence on surface roughness, viscosity and density of the liquid. The magnitude of specific loss factor is found to be more in case of viscous liquid. It is also noticed that magnitude of phase velocity in case of silicon semiconductor material with thermal conductivity ratio (k‾) and wave number(R) is found to be large than that for germanium semiconductor material.

Acknowledgments

The authors are extremely thankful to the reviewers for their deep interest and their valuable suggestions for the improvement of this work.

Appendix

The quentatities used in equations (17) and (19) are given by

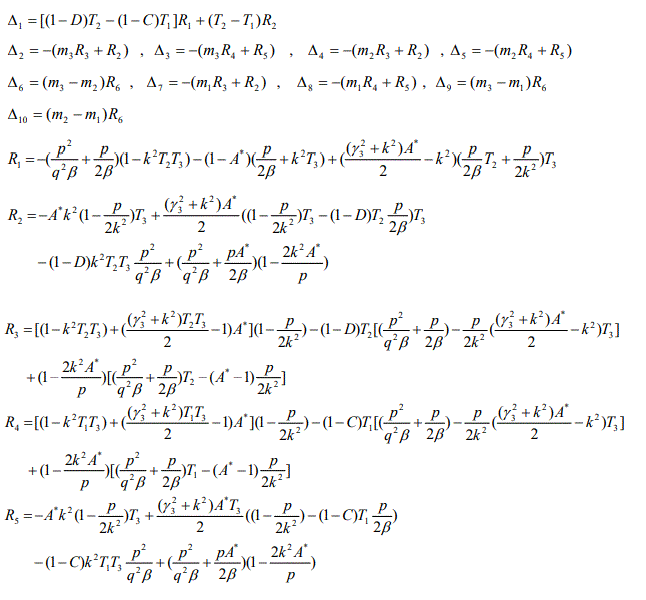
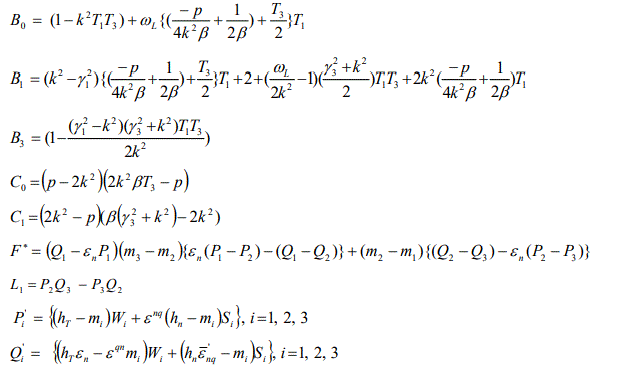
References

1. Graff KF. Wave motion in elastic solids. Dover. New York; 1991.   
2. Nowacki W. Dynamic problems of thermoelasticity, Noordoff, Leyden, The Netherlands 1975.   
3. Maruszewski B. Electro-magneto-thermo-elasticity of extrinsic Semiconductors classical irreversible thermodynamic Approach. Arch Mech. 1986a; 38: 71-82.   
4. Maruszewski B. Electro-magneto-thermo-elasticity of extrinsic semiconductors, extended irreversible thermodynamic Approach. Arch Mech. 1986b; 38: 83-95   
5. Maruszewski B. Coupled evolution equations of deformable semiconductors. Int J of Eng Scie. 1987a; 25(2): 145-153. doi: 10.1016/0020-7225(87)90002-4   
6. Maruszewski B. Thermodiffusive surface waves in semiconductors. J Acoust Soc Am. 1989; 85(5): 1967-1977. doi: 10.1121/1.397850   
7. Maruszewski B. Heat and charge carrier relaxation in deformable semiconductors, in electro magneto-mechanical interactions in deformable solids and structures, edited by Yamamo Y. to and Miya K. (Northland, Amsterdam) 1987b.   
8. Sharma JN, Thakur N. Plane harmonic elasto-thermodiffusive waves in materials. J Mech Mater and Struct. 2006; 1: 813-835.   
9. Sharma JN, Thakur N, Walia V. Propagation of thermoelasto-diffusive surface acoustic waves in semiconductor materials. Asian J Chem. 2006; 18(5): 3329-3334.   
10. Sharma JN, Thakur N. Propagation of thermoelasto-diffusive surface acoustic waves in semiconductor materials. J Therm Stresses. 2007; 30: 357-380.   
11. Sharma JN, Sharma I, Chand S. Elasto-thermodiffusive surface waves in a semiconductor material half-space underlying a fluid with varying temperature. J Therm Stresses. 2008; 31: 956-957. doi: 10.1080/01495730802250524   
12. Sharma I, Sharma JN, Chand S. A coustodiffusive Rayleigh waves in a semiconductor materials half space in contact with fluid medium. Proc Natl Acad Sci India Sect. A. 2009; 79: 280-289.   
13. Sharma JN, Sharma I, Chand S. Acousto thermodiffusive interfacial waves in a semiconductor loaded with viscous fluid. J Appl Math Mech. 2010; 6(3): 21-42.   
14. Sharma J.N., Sharma A. Reflection of acoustodiffusive waves from the boundary of a semiconductor half-space. J Appl Phys. 2010; 108: 033712-033723.   
15. Sharma A, Sharma JN, Sharma YD. Modelling Reflection and Transmission of Acoustic Waves at a Semiconductor: Fluid Interface. J Adv Acoust Vib. 2012; 1-10. doi: 10.1155/2012/637912   
16. Sharma I. Effect of liquid loading lamb wave in a semiconductor materials plate. J Appl Math Mech. 2014; 10(10): 50-73.   
17. Kansh PL, Bartiaans GJ. Piezoelectric crystal as detector in liquid chromatography. Anal Chem. 1980; 52(12): 1929-1931. doi: 10.1021/ac50062a033   
18. Josse F, Shana Z, Radtke DE, Haworth DT. Analysis of Piezoelectric BulkAcoustic -Wave Resonators and detectors in viscous conductive liquid. EEE Trans Ultrason Ferroelectr Freq Control. 1990; 37: 359-368.   
19. Many A, Goldstein J, Grover NB. Semiconductor Surfaces: NorthHolland: Amsterdam 1965.   
20. Zambuto M. Semiconductors devices. Mcgraw-Hill Book Company. New York; 1989.   
21. Sze SM. Physics of Semiconductors Devices. A Wiley-Intersciences Publication, John Wilky and Sons, New York; 1981.   
22. Lal S. Fundamental Physics, S. Vikas and Co., Educational Publishers, New Delhi 1995.   
23. Nakamura M, Tamura K, Murakami S. Isotope effects on thermodynamics properties: Mixtures of x D O or H O x CH CN 2 2 3 ( ) + (1−) at 298.15. Thermochim Acta. 1995; 253: 127-136.   
24. Cengel YA, Cimbala JM. Fluid Mechanics. Tata McGrW-Hill, New Delhi; 2006.   
25. Crabtree A. Siman-Tov M. Thermo physical properties of saturated light and heavy water for advanced neutron source applications. Oak Ridge National Laboratory managed by Martin Marietta energy systems, INC. U.S. Department of energy 1993.