Abstract

Different from fully mechanized mining face, there is the combination of top-coal and immediate roof which can be regards as a special material acting as cushion layer to bear the overburden load in the long wall top coal caving (LTCC) face. Further, the vertical stress causing the deformation of coal-rock combination material (CRCM) is transmitted to hydraulic support. In this paper, the elastic modulus and foundation coefficient of CRCM are calculated and analyzed in both conditions of CRCM with or without contact angle. The results show that the height of coal and rock, the elastic modulus of coal and rock, respectively, play vital roles on the elastic modulus and foundation coefficient of CRCM. Moreover, the height of coal and rock have similar influence on the characteristics of combination material. Meanwhile, it also indicates that the elastic modulus of coal and rock appear to exert similar effects on the behaviors of combination material. In the condition of CRCM with contact angle, the relationship between the elastic modulus and foundation coefficient of CRCM with the effective height ratio of coal and rock or contact angle is determined on the relative value of the elastic modulus of coal and rock, respectively. However, the influence of the contact angle on the elastic modulus and foundation coefficient of CRCM is not significant. Importantly, the analytic solution and change law for the elastic modulus and foundation coefficient of CRCM with the parameters of coal-rock combination are determined which provides the theoretical rational for further determining the work resistance of hydraulic support, selecting the type of hydraulic support and researching the moving rules of overlying strata at LTCC face.

Keywords: Coal-rock combination; Elastic modulus; Foundation coefficient; Theoretical calculation.

Introduction

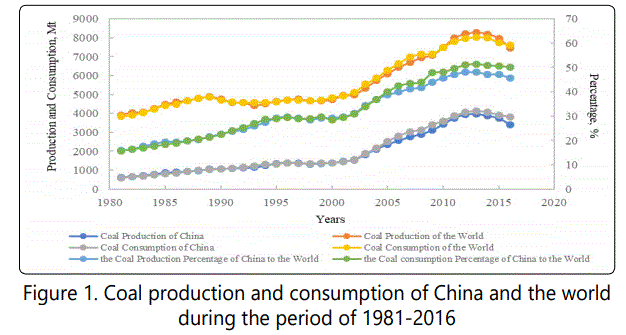
China is the largest coal producers and consumers in the world. As shown in Fig. 1, there is similar tendency both of production and consumption for China and the world which indicates that China plays a vital role on the total coal economic in the world. The coal production and consumption percentage of China to the world is approximately 50% in recent years [1]. Meanwhile, in the exploration of coal seam storage in China, thick coal seams (thickness≥3.5m) are rich in reserves accounting for approximately 44% of all coal seam reserves. Moreover, the production of thick coal seams is roughly 45% of the total coal production [2-5]. It can be seen that the thick coal seam has obvious advantage in resource reserves and practical production in China [6-8].

At present, three kinds of methods with slice mining, high mining height mining and LTCC mining have been performed to exploit the resource of thick coal seam. Among these methods, LTCC has the advantages of exploitation technology which cannot be matched by others. Especially, LTCC can greatly reduce the number of inverted work face and material consumption, correspondingly decreasing the cost of per ton coal. Importantly, LTCC can adapt complex geological conditions and the conditions of coal seam occurrence as a result the fully mechanized mining can be achieved through LTCC mining with the advantages of technical and economic obviously in steeply inclined and extremely thick coal seams. Therefore, LTCC has a dominant position in the mining of thick coal seams [9-13]. It should be noted that the coal miner in other countries by using LTCC mining is relatively less compared with China due to the difference of the conditions of coal seam occurrence. The literatures on thick coal seam mining with LTCC mining technology or similar methods are mainly concentrated on several countries, such as Australia, India, Turkey, Russia, Slovenia [14-18].

In the LTCC working face, the determination of hydraulic support has vital role for the selection of reasonable support type which is the basis for the three machines equipment matching applied, and it is also the core content of the relationship between support and surrounding rock, which is extremely critical for roof management and achieving safe mining in stope. Thus, it is the importance of obtaining the reasonable theory calculation for overlying strata loading transmitting on support [19-24]. It is believed that the factors influencing on the determination of support working resistance mainly consist of geological factors and engineering factors [25-26]. In details, the geological factors mainly include the characteristics of mining height, overlying strata and top-coal. Moreover, the sufficient support working resistance is required as a result of increasing in vertical stress in working face with the increasing of the depth of coal seam causing more overburden loading. In addition, if the coal seam is in the condition of shallow thin bedrock, the main roof is unstable and unable to form bearing structure causing its loading acting on support fully and further increasing supporting work resistance. Meanwhile, the overburden loading transmitting on support decreases with the increasing of coal seam dip. In terms of engineering factors, these mainly include extractioncaving ratio, face length, roadway layout and the treatment methods for support. In details, the mining space increases with the increasing of extraction-caving ratio if coal seam thickness keeps constant in working face as a result the reduce of cushion effect caused by top-coal on the failure of overlying strata. Therefore, the overburden loading on support increases and the maximum support working resistance can bear this value. In general, the relationship between the support work resistance and extraction-caving ratio is not obvious [27]. However, this relationship is more reinforced with coal seam thickness increasing.

Compared with other mining methods, there is a layer of top-coal with low strength between support and overlying strata in LTCC mining acting as cushion for bearing overburden loading and then transmitting on support. Obviously, the cushion effect plays a key role in controlling roof subsidence and ensuring support working state as well as influencing on the relationship between support and surrounding rock. In currently literatures, the determination methods of support working resistance usually only consider top-coal or overlying strata. Many experts and scholars have conducted extensive research on the characteristics of deformation and failure of single coal or rock under uniaxial or triaxial loading condition by using acoustic emission, infrared thermal imaging and other equipment in laboratory [28-33]. In fact, the behaviors of immediate roof are similar to that of top-coal. Therefore, it is more reasonable to consider top-coal and immediate roof as combination material rather than taking into account each part separately influencing on the expression of support working resistance and moving rules of overlying strata in LTCC working face. In recent years, the mechanical properties of coal-rock combination material have been paid more attention to study by many literatures and a series of notable results are achieved through experiment tests [34-38]. Most of these results focused on the field of energy dissipation connecting with the mechanics of rock burst. However, there are few documents on CRCM through analytic solution and further building the relationship between combination material and the determination of support working resistance on LTCC working face. Therefore, top-coal and immediate roof is regard as combination material in this paper, and then the theory solution of the mechanical properties of CRCM as the whole cushion layer are described and the change rules of the elastic modulus and foundation coefficient of CRCM with coal thickness, rock thickness, the elastic modulus of coal and rock are analyzed, which lay theoretical foundation for determining support working resistance by considering the mechanical properties of CRCM in LTCC working face.

Theoretical Solution of Mechanical Properties of CRCM

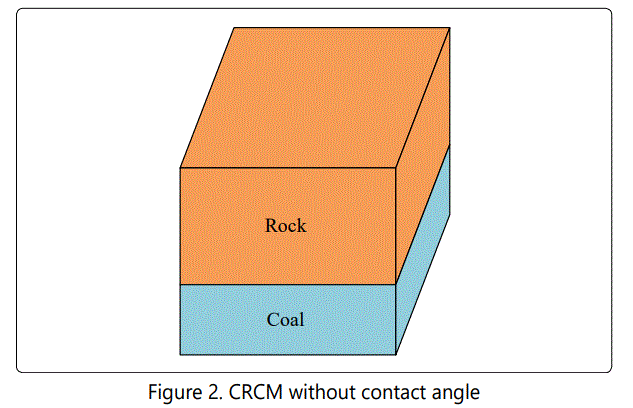
CRCM without Contact Angle

The schematic diagram of CRCM as a cube without contact angle is shown in Figure 2. In order to facilitate theoretical calculation, the various parameters of CRCM are listed in table 1.

Therefore, the height ratio of coal to rock, the stiffness and pull-pressing rigidity of CRCM can be expressed as follow.

Further, through equations (2) and (3), the relationship between the stiffness and pull-pressing rigidity of CRCM can be obtained as follows.

Similarly, the relationship between the stiffness and pull-pressing rigidity of coal or rock can also be expressed as follow.

In addition, according to Hooke's Law, the vertical force causes a certain deformation for each part in CRCM.

And then combining with equations (5) ~ (7), it can be concluded as follow.

It should be noted that the stiffness of CRCM can also be obtained as equation (9) through the series stiffness formula of coal and rock separately.

Thus, combining with equations (4) and (9), the pullpressing rigidity of CRCM can be expressed as follow.

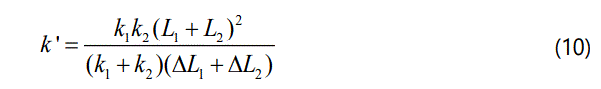
Bringing equations (5) ~ (6) into equation (10), there can be obtained the expression of the pull-pressing rigidity of CRCM.

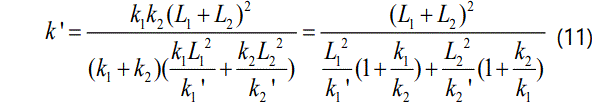
Both numerator and denominator of equation (11) are divided by L₂² to get the new formula as follow.

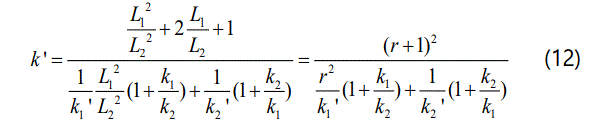
However, the ratio of the stiffness of coal to rock can be known from equation (8).

Further, bringing equation (13) into equation (12) and getting the final expression of CRCM's pull-pressing rigidity as follow.

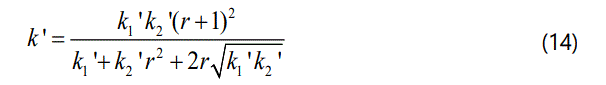
From the relationship between elastic modulus and pullpressing rigidity, the elastic modulus of CRCM can be obtained as equation (15).

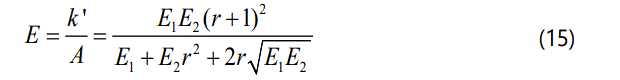
According to elastic foundation beam model, the foundation coefficient of CRCM k₀ can be calculated approximately and expressed as follow.

Where H is CRCM thickness, H=L₁+L₂; E is the elastic modulus of CRCM.

CRCM with Contact Angle

The schematic diagram of CRCM as a cube with contact angle α is shown in Fig. 3, and the parameters of CRCM are listed in table 2.

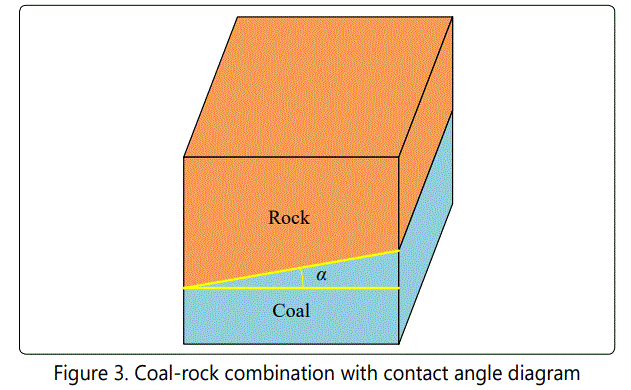
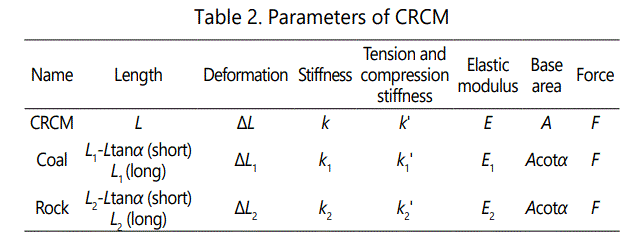
When the interface of coal and rock has a certain angle, the height ratio of coal to rock in CRCM is not effectively represented by single side length. Therefore, it is necessary to define the effective height ratio of coal to rock. Firstly, the ratio of the cross-section of single material paralleling to the direction of axial force to the length of CRCM is called the effective height of single material. Further, the effective height ratio of CRCM can be expressed as the ratio of the effective height of coal to that of rock. The coordinate of coal at the lower part of CRCM is established as shown in Figure 4 (a).

Therefore, the equation of interface line can be expressed as equation (17) through both sides height of coal.

Similarly, the coordinate can also be built based on the upper part of CRCM as shown in Fig. 4 (b).

Thus, the equation of interface line can also be obtained with another expression as follow.

According to the definition of the effective height of single material, it can be expressed as follow.

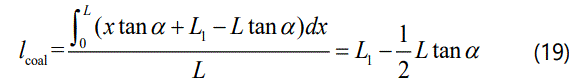
Where l_coal is the effective height of coal.

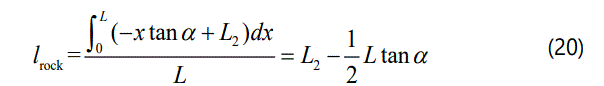
Where l_rock is the effective height of rock. Thus, the effective height ratio of coal to rock for CRCM is expressed as equation (21) due to the above definition.

Further, combining with equations (4) ~ (15) and (19) ~ (21), the elastic modulus of CRCM with contact angle can be obtained as follow.

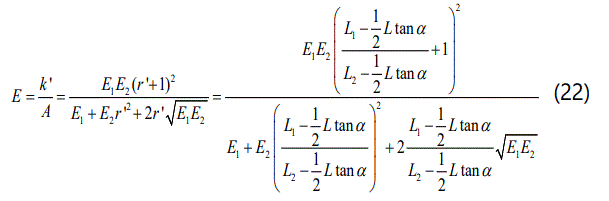
According to the geometric relationships of CRCM, the corresponding equation can be obtained as follow.

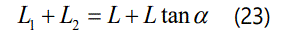
Let 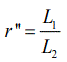and simplifying equation (22) to get the expression of the elastic modulus of CRCM as follow.

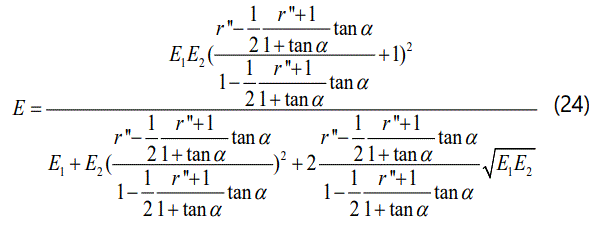
Let 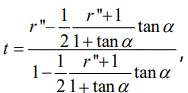, then the elastic modulus of CRCM with contact angle can be finally expressed as follow.

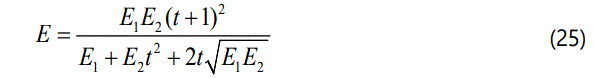
It should be noted that t is related to the three parameters of the long side of coal or rock and the contact angle of interface. From equation (16), the value of CRCM's foundation coefficient with contact angle between coal and rock is also acquired.

Comparative Analysis of CRCM's Elastic Modulus and Foundation Coefficient

CRCM without Contact Angle

Theoretical solution shows that the coal height or rock height and the elastic modulus of coal or rock can affect the mechanical properties of CRCM without contact angle, that is to say, which the interface of CRCM is horizontal. The details of changing rules for these factors influencing on the elastic modulus and foundation coefficient of CRCM will be analyzed as follow.

Coal height

In order to explain the influence of coal's height on the elastic modulus and foundation coefficient of CRCM, the height of rock is selected as 4m as well as the three conditions of the coal's elastic modulus are considered to be smaller, greater than or equal to the rock's elastic modulus, respectively. That is to say, the elastic modulus of coal and rock are 4GPa and 6GPa, 6GPa and 4GPa, 6GPa and 6GPa, respectively. According to equations (15) and (16), the variation of elastic modulus and foundation coefficient of CRCM with coal height which is range from 0 to 10 m is shown in Figure 5.

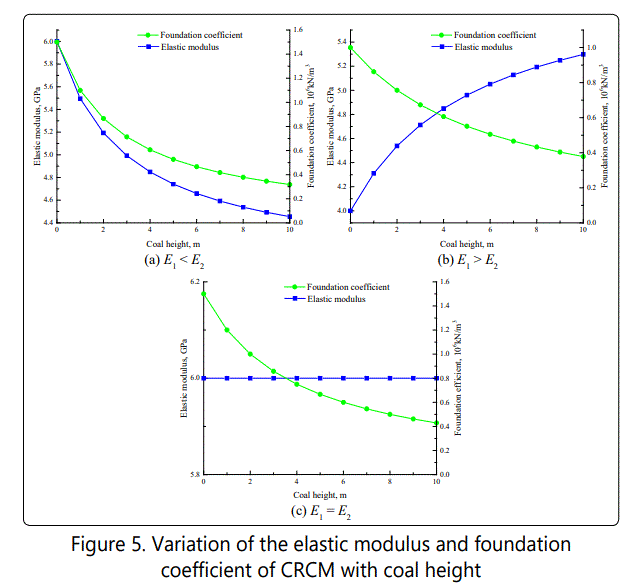
According to Figure 5, it can be seen that the change of elastic modulus of CRCM shows different trends with the increasing of coal height under three conditions. Especially, the trend decreases in the condition of coal's elastic modulus smaller than rock's elastic modulus which is opposite to another condition of coal's elastic modulus greater than rock's elastic modulus. However, the trend increases or decreases slowly with the increasing of coal height. In addition, the elastic modulus of CRCM keeps constant if the coal's elastic is equal to rock's elastic modulus.

In terms of the change of foundation coefficient of CRCM, the trends are quite different from the change of modulus of CRCM as a result of the increasing of coal height causing CRCM height increasing as well. Therefore, the trends all decreases with the increasing of coal height under three conditions regardless of the relative relationship between the elastic modulus of coal and the elastic modulus of rock.

Compared with single rock material, the presence of a small amount of coal in combination material has a significant effect on its mechanical properties. When coal's elastic modulus is not a same value with that of rock, a greater influence on the elastic modulus of CRCM than the foundation coefficient of CRCM with the changing of coal height can be indicated. Conversely, the foundation coefficient of CRCM has markedly changing with the elastic modulus of coal equaling to the elastic modulus of rock. Especially, when the height ratio of coal to rock is less than 2, the mechanical properties of CRCM are most affected with the changing of coal height. Meanwhile, the change of the elastic modulus and foundation coefficient of CRCM is approximately linearly with coal height when this height ratio exceeds a certain value.

Rock height

To gain insight into the influence of rock height on the elastic modulus and foundation coefficient of CRCM, coal height is chosen to be 4m, and three conditions of the relative relationship between rock's elastic modulus and coal's elastic modulus are considered to analyze. That is to say, the coal's elastic modulus and rock's elastic modulus are selected as 4GPa and 6GPa, 6GPa and 4GPa, 6GPa and 6GPa, respectively. Therefore, the variation of the elastic modulus and foundation coefficient of CRCM with rock height can be revealed in Figure 6.

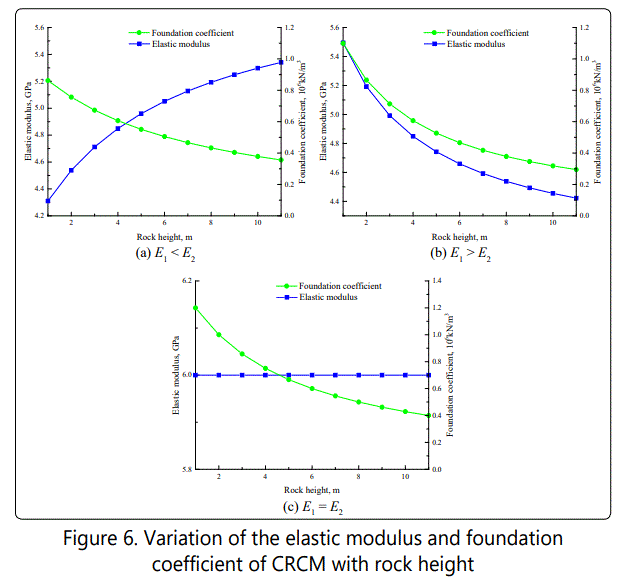
From Figure 6, it can be seen that the variation of the elastic modulus of CRCM with the increasing of rock height is opposite to that of coal height when the value of coal's elastic modulus is different from rock's elastic modulus. In other words, the trend of the elastic modulus of CRCM with the increasing of rock height increases under the condition of the coal's elastic modulus smaller than rock's elastic modulus and decreases under the opposite condition. Similarly, the elastic modulus of CRCM with the increasing of rock height remains constant when the coal's elastic modulus is equal to rock's elastic modulus.

In terms to the foundation coefficient of CRCM, due to the increasing of rock height also causing CRCM height increasing, the change trend all decreases under three conditions regardless of the relative relationship between the elastic modulus of coal and the elastic modulus of rock.

Compared with single coal material, the presence of a small amount of rock in combination material has obvious effect on the elastic modulus and foundation coefficient of CRCM especially when the rock's elastic modulus is not a same value with coal's elastic modulus. In details, expect for the condition of both the elastic modulus of coal and rock is same, the changing of rock height has played more noticeable role on the elastic modulus of CRCM than the foundation efficient of CRCM. Moreover, when the height ratio of rock to coal is less than 2, the mechanical properties of CRCM are most affected with the changing of rock height. In addition, the elastic modulus and foundation coefficient of CRCM are almost linearly with rock height when the height ratio of rock to coal exceeds a certain value.

Through comparison and analysis of the changing trend, it can be indicated that both coal and rock height have similar effects on the mechanical properties of CRCM. Therefore, it can be considered that there is no obvious effect on the mechanical characteristics of CRCM whether the combination form is coalrock or rock-coal. That is to say, the behaviors of combination material are irrelevant to the relative location of coal and rock.

The elastic modulus of coal

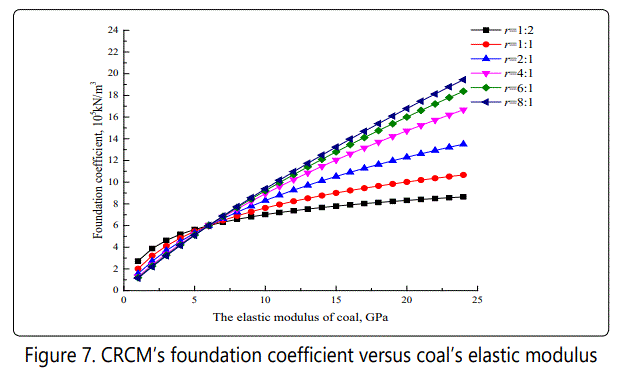
In order to analysis the effect of coal's elastic modulus on the elastic modulus and foundation coefficient of CRCM, the changing of coal's elastic modulus is range from 1GPa to 24GPa, which rock's elastic modulus remains at 6GPa. Meanwhile, taking CRCM height as 10m for example, the corresponding height ratio of coal to rock is 1:2, 1:1, 2:1, 4:1, 6:1, and 8:1, respectively. It should be noted that the changing trend of elastic modulus of CRCM is the same with the foundation coefficient of CRCM under the condition of CRCM height keeping constant according to equations (15) to (16). Therefore, taking the changing trend of the foundation coefficient of CRCM as example, a comprehensive analysis about variation of CRCM's foundation coefficient with coal's elastic modulus is shown in Figure 7.

According to Figure7, it indicated that the foundation coefficient of CRCM increases with the increasing of coal's elastic modulus regardless of the height ratio of coal to rock and the tendency to change reduces. In details, the changing of the foundation coefficient of CRCM is nonlinearly with the increasing of coal's elastic modulus when coal's elastic modulus is smaller than rock's elastic modulus, while this changing is approximately linearly with coal's elastic modulus increasing under the condition of coal's elastic modulus greater than rock's elastic modulus. Meanwhile, when the height ratio of coal to rock is relative small, the changing of coal's elastic modulus has remarkable effect on the mechanical characteristics of CRCM under coal's elastic modulus smaller than rock's elastic modulus. On the contrary, there is no significant effect on the mechanical characteristics of CRCM under coal's elastic modulus greater than rock's elastic modulus. On the other hand, when the height ratio of coal to rock is relative large, the influence of the relative relationship between coal's elastic modulus and rock's elastic modulus on the foundation coefficient of CRCM becomes less prominent. That is to say, there is remarkable effect on the foundation coefficient of CRCM in the entire range of coal's elastic modulus.

The elastic modulus of rock

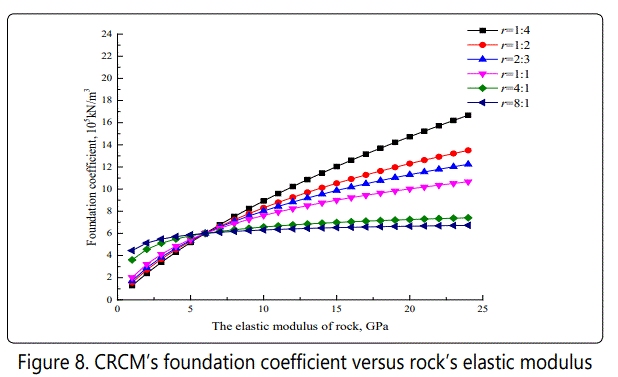
Similarly, for studying the variation of the elastic modulus and foundation coefficient of CRCM with rock's elastic modulus, the different rock's elastic modulus is considered with the range from 1GPa to 24GPa, while coal's elastic modulus keeps with 6GPa. Meanwhile, CRCM height is assumed as 10m, and the corresponding height ratio of coal to rock is 1:4, 1:2, 2:3, 1:1, 4:1, and 8:1, respectively. It should be noted that the variation of the elastic modulus of CRCM is similar to the foundation coefficient of CRCM under the condition of CRCM height remaining constant according to equation (16). Therefore, taking the variation of the foundation coefficient of CRCM with rock's elastic modulus as example, the comprehensive analysis is shown in Figure 8.

According to Figure 8, it can be seen that the foundation coefficient of CRCM increases with the increasing of rock's elastic modulus. In details, the changing of the foundation coefficient of CRCM is nonlinearly increasing with the increasing of rock's elastic modulus under the condition of rock's elastic modulus smaller than coal's elastic modulus, while this changing is linearly increasing with the increasing of rock's elastic modulus under the opposite condition. In addition, the influence of rock's elastic modulus on the foundation coefficient of CRCM always exists with the changing of rock's elastic modulus when the height ratio of coal to rock is relative small. However, this obvious trend can only be revealed under the condition of rock's elastic modulus smaller than coal's elastic modulus when the height ratio of coal to rock is relative large. In general, the reduction impact of rock's elastic modulus on the foundation coefficient can be found with the increasing of the height ratio of coal to rock.

CRCM with Contact Angle

When there is a certain angle with the interface of CRCM, the effect of coal's elastic modulus or rock's elastic modulus on the elastic modulus and foundation coefficient of CRCM is similar to that of CRCM without contact angle according to compare the equation (25) with equation (15) and combine with equation (16). Therefore, there is no much detail about the influence of coal's elastic modulus or rock's elastic modulus on the elastic modulus and foundation coefficient of CRCM with contact angle here. On the other hand, the effective height ratio of coal to rock and the value of contact angle have different impact on the elastic modulus and foundation coefficient of CRCM due to the existence of contact angle on CRCM. Therefore, in order to analyze the variation of elastic modulus and foundation coefficient of CRCM with the changing of the effective height ratio of coal to rock and contact angle, the CRCM height is assumed as 10m with the effective height ratio of coal to rock ranging from 0.4 to 2.0 and contact angle ranging from 0° to 26°. It should be noted that the changing trend of CRCM's elastic modulus is similar to that of the foundation coefficient of CRCM according to equation (16). Therefore, taking the variation of the foundation coefficient of CRCM with the effective height ratio and contact angle as example is described and analyzed. In addition, three conditions of the relative relationship between coal's elastic modulus and rock's elastic modulus are considered with 4GPa and 6GPa, 6GPa and 4GPa, 6GPa and 6GPa, respectively. The details are as follows.

The effective height ratio of CMCR with contact angle

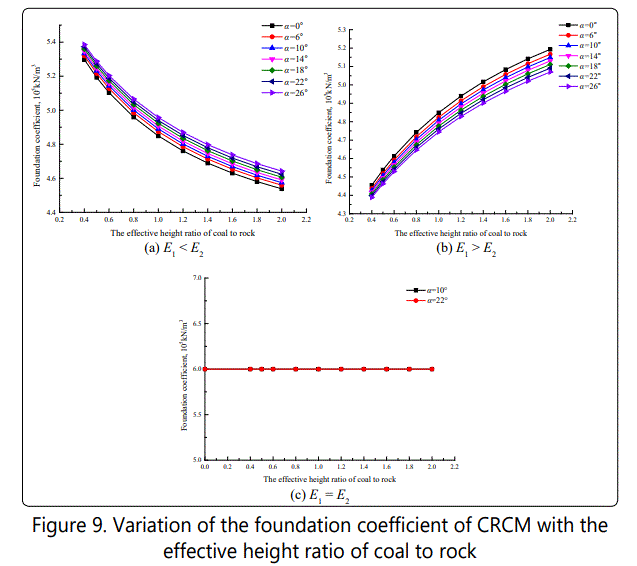
As shown in Figure 9, the variation of the foundation coefficient of CRCM with the effective height ratio of coal to is reflected when the contact angle of CRCM is 0°, 6°, 10°, 14°, 18°, 22° and 26°, respectively. It indicated that the foundation coefficient of CRCM decrease with the increasing of the effective height ratio of coal to rock on all contact angle when coal's elastic modulus is smaller than rock's elastic modulus, while this trend is opposite when coal's elastic modulus is greater than rock's elastic modulus. However, these changing trends slow down. Therefore, the foundation coefficient of CRCM is affected greatly within the lower effective height ratio of coal to rock when coal's elastic modulus is different from rock's elastic modulus. By contrast, the foundation coefficient of CRCM keeps constant with the increasing of the effective height ratio of coal to rock under the condition of coal's elastic modulus equaling to rock's elastic modulus.

Contact angle

Figure 10. shows the changing trend of CRCM's foundation coefficient with the changing of contact angle in the range of effective height ratio from 0.4 to 2.0. It can be found that the variation of CRCM's foundation coefficient is approximately linearly with contact angle when coal's elastic modulus is smaller than rock's elastic modulus, while this trend is opposite under the condition of coal's elastic modulus greater than rock's elastic modulus. However, there is no changing for CRCM's foundation coefficient with contact angle when coal's elastic modulus is equal to rock's elastic modulus due to the similar mechanical properties both coal and rock at this condition.

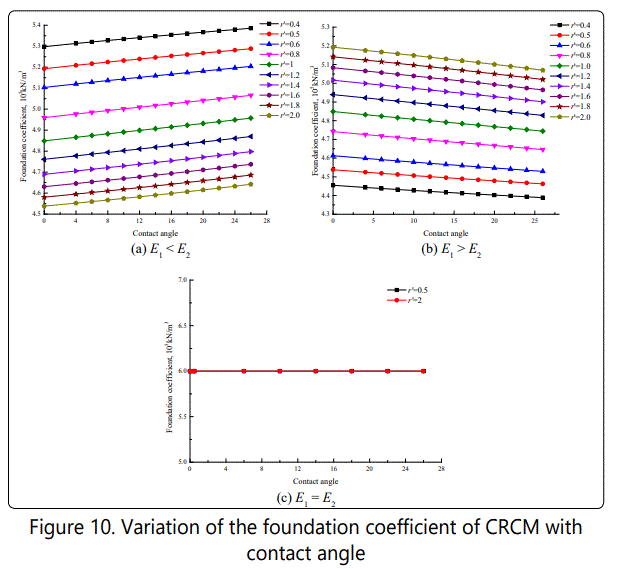
Although the relationship of foundation coefficient of CRCM with the effective height ratio of coal to rock and contact angle is described as above, the influence of contact angle on the foundation coefficient of CRCM is not remarkable on the whole. Meanwhile, through analyzing the influence factors of contact angle and the effective height ratio of coal to rock on the foundation coefficient of CRCM, the results show that the impact of the effective height ratio of coal to rock on the foundation coefficient of CRCM is greater than that of contact angle.

Discussion

Based on elastic foundation beam model, it is of great importance to describe the elastic modulus and foundation coefficient of CRCM for determining support working resistance in LTCC face. Therefore, this paper describes the variation of elastic modulus and foundation coefficient of CRCM with coal height, rock height, coal's elastic modulus and rock's elastic modulus without contact angle as well as the effective height ratio and contact angle with contact angle. Results indicate that all factors mentioned above have certain degree effect on the mechanical properties of CRCM. Although there are some rules revealed by theory solutions and further analysis, some limitations should also be admitted. In the study, both coal and rock are considered as ideal elastic body. In fact, as top-coal caving in LTCC face, both top-coal and rock gradually broken with the process of mining. Meanwhile, it should be paid more attention on the law of energy transfer and dissipation in cushion layer as well as the preparation of joint fracture samples in the future theoretical studies and laboratory tests. However, in summary, the analysis and theoretical solution of the elastic modulus and foundation coefficient of CRCM lay theoretical foundation for the effect of the mechanical properties of CRCM on determining support working resistance in LTCC face. Authors also carried out experiments test to research the effect of coal height, rock height, coal's elastic modulus, rock's elastic modulus, the effective height ratio of coal to rock, and contact angle on the elastic modulus of CRCM. In addition, the theoretical solution of support working resistance in LTCC face have been solved combined with the results of this paper and based on elastic foundation beam model. These results will be described and analysed in other articles.

Summary and Conclusions

This paper mainly describes the process of theorical solution for the elastic modulus and foundation coefficient of CRCM and analyses the influence factors of coal height, rock height, coal's elastic modulus, rock's elastic modulus, the effective height ratio of coal to rock, and contact angle on the elastic modulus and foundation coefficient of CRCM. The conclusions can be obtained as follow.

1. Building CRCM without contact angle and with contact angle model, the corresponding theorical solution of the elastic modulus and foundation coefficient of CRCM can be obtained under both conditions.

2. Both coal height and rock height have quite different effect on the elastic modulus and foundation coefficient of CRCM without contact angle. The elastic modulus of CRCM decreases with the increasing of coal height when coal's elastic modulus is smaller than rock's elastic modulus and increases with the increasing of coal height when coal's elastic modulus is greater than rock's elastic modulus. However, the opposite trend of CRCM's elastic modulus with the increasing of rock height can be revealed under the same condition. In terms of the foundation coefficient of CRCM, it always decreasing with the increasing of coal height or rock height. And all trends slow down.

3. The elastic modulus and foundation coefficient of CRCM increase with the increasing of coal's elastic modulus or rock's elastic modulus and the tendency to change reduces. In addition, the reduction impact of coal's elastic modulus on the elastic modulus and foundation coefficient of CRCM can be found with the decreasing of the height ratio of coal to rock, while the opposite result which the reduction impact of rock's elastic modulus on the elastic modulus and foundation coefficient of CRCM with the increasing of the height ratio of coal to rock can be indicated.

4. When there is contact angle for CRCM, the similar changing trend of the elastic modulus and foundation coefficient of CRCM can be described with that of CRCM without contact angle.

5. The elastic modulus and foundation coefficient of CRCM decrease with the increasing of the effective height ratio of coal to rock on all contact angle when coal's elastic modulus is smaller than rock's elastic modulus, while this trend is opposite when coal's elastic modulus is greater than rock's elastic modulus. And these changing trends slow down.

6. The variation of the elastic modulus and foundation coefficient is approximately linearly with contact angle when coal's elastic modulus is smaller than rock's elastic modulus, while this trend is opposite under the condition of coal's elastic modulus greater than rock's elastic modulus. However, there is no apparent effect of contact angle on the elastic modulus and foundation coefficient of CRCM on the whole. In addition, the results show that the impact of the effective height ratio of coal to rock on the mechanical properties of CRCM is greater than that of contact angle.

Acknowledgement

The authors wish to acknowledge the support from China Scholarship Council (CSC).

References

1. BP. BP Statistical review of world energy. British Petroleum. 2017, London.   
2. Wang JC. Engineering practice and theoretical progress of top-coal caving mining technology in China. Journal of China Coal Society. 2018; 43(1): 43-51.   
3. Wang JC, Yang SL, Li Y, Wei Lk, Liu HH, et al. Caving mechanisms of loose top-coal in longwall top-coal caving mining method. International Journal of Mining Science and Technology. 2014; 27(6): 1081-1085. doi: 10.1016/j. ijrmms.2014.04.024   
4. Wu J. Theory and practice of sub-level caving method in China. Journal of China Coal Society. 1991; 16 (3): 1-11   
5. Fan YC. A revolution of coal mining method in thick coal seam in China. Innovative development of theory and practice of full mechanized caving coal technology. Proceedings of the 30th Anniversary of Fully Mechanized Top Coal Caving, Beijing: China Coal Industry Publishing House. 2012; 3-7.   
6. Kong LH, Jiang FX, Wang CW, et al. Study of reasonable working resistance of support in fully-mechanized sublevel caving face in extra-thick coal seam. Chinese Journal of Rock Mechanics and Engineering. 2010; 29 (11): 2312-2318.   
7. Wang JC, Liu F, Wang L. Sustainable coal mining and mining sciences. Journal of China Coal Society. 2016; 41(11): 2651-2660.   
8. Ma LQ, Cao XQ, Li QQ. The support stability mechanism in dip direction of fully mechanised working face with big dip angle considering the strike angle. International Journal of Oil, Gas and Coal Technology. 2015; 9(1): 61-78. doi: 10.1504/IJOGCT.2015.066929   
9. Le TD, Oh J, Hebblewhite B. A review of cavability evaluation in longwall top coal caving. International Journal of Mining Science and Technology. 2017; 27 (6): 907-915.   
10. Huang BX, Wang YZ, Cao SG. Cavability control by hydraulic fracturing for top coal caving in hard thick coal seams. International Journal of Rock Mechanics and Mining Sciences. 2015; 74: 45-57. doi: 10.1016/j. ijrmms.2014.10.011   
11. Vakili A, Hebblewhite BK. A new cavability assessment criterion for longwall top coal caving. International Journal of Rock Mechanics and Mining Sciences. 2010; 47(8): 1317-1329. doi: 10.1016/j.ijrmms.2010.08.010   
12. Alehossein H, Poulsen BA. Stress analysis of longwall top coal caving. International Journal of Rock Mechanics and Mining Sciences. 2010; 47 (1): 30-41. doi: 10.1016/j.ijrmms.2009.07.004   
13. Kumar R, Singh AK, Mishra AK, et al. Underground mining of thick coal seams. International Journal of Mining Science and Technology. 2015; 25(6): 885-896. doi: 10.1016/j.ijmst.2015.09.003   
14. Mitchell GW. Longwall mining-Chapter 15. Australasian coal mining practice. Australasian Institute of Mining and Metallurgy. 2009; 340-373.   
15. Singh R, Singh TN. Investigation into the behaviour of a support system and roof strata during sublevel caving of a thick coal seam. Geotechnical and Geological Engineering. 1999; 17 (1): 21-35. doi: 10.1023/A:1008853914726   
16. Ozfirat MK, Simsir F, Gonen A. A brief comparison of longwall methods used at mining of thick coal seams. 19th International Mining Congress and Fair of Turkey, IMCET. 2005.   
17. Klishin SV, Klishin VI. Management of the processes of flow of rock mass at underground mining in sublevel caving systems. Proceedings of the 22nd World Mining Congress. 2011; 1-6.   
18. Jeromel G. Numerical simulation of top caving processes in coal mining. Ljubljana, University of Ljubljana. 2004.   
19. Nie W, Cheng WM, Zhang L, et al. Optimization Research of Hydraulic Support in Fully Mechanized Caving Face. International Symposium on Safety Science and Technology. 2014; 84: 770-778. doi: 1016/j.proeng.2014.10.495   
20. Hao XJ, Xu JL, Zhu WB, et al. Determination of the reasonable support working resistance. The 6th International Conference on Mining Science & Technology. 2009; 1(1): 1398-1405. doi: 10.1016/j.proeps.2009.09.216   
21. Wang JC, Yu B, Kang HP, et al. Key technologies and equipment for a fully mechanized top-coal caving operation with a large mining height at ultra-thick coal seams. International Journal of Coal Science & Technology. 2015; 2(2): 97-161. doi: 10.1007/s40789-015-0071-4   
22. Kirzhner F, Rozenbaum M. Behavior of the working fluid in mechanized support in permafrost. Journal of Cold Regions Engineering. 2001; 15(3): 170-185. doi: 10.1061/(ASCE)0887-381X(2001)15:3(170)   
23. Ruppel U, Langosch U. New method for dimensioning of shield support to improve longwall roof control. Journal of Mines, Metals and Fuels. 2006; 54 (8): 179-184.   
24. Cheng ZB, Kong DZ, Yang JH. The breaking characteristics of thick-hard roof and determination of support capacity in fully mechanized caving face. Journal of Mining Science and Technology. 2016; 1(2): 172-180.   
25. Cheng ZB. Load estimation method of fully mechanized caving face support. Safety in Coal Mines. 2015; 46(12): 210-213.   
26. Cheng ZB, Determination on support work resistance for fully mechanized caving face with multi-gangue stratum. Safety in Coal Mines. 2016; 47 (4): 222-225.   
27. Qian MG, Shi PW. Ground pressure and strata control. China University of Mining and Technology Press. 2003.   
28. Masri M, Sibai M, Shao JF, et al. Experimental investigation of the effect of temperature on the mechanical behavior of Tournemire shale. International Journal of Rock Mechanics & Mining Sciences. 2014; 70: 185- 191. doi: 10.1016/j.ijrmms.2014.05.007   
29. Labuz JF, Zang A. Mohr-Coulomb Failure Criterion. Rock Mechanics and Rock Engineering. 2012; 45 (6): 975-979. doi: 10.1007/s00603-012-0281-7   
30. Lockner D. The role of acoustic emission in the study of rock fracture. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. 1993; 30(7): 893-899. doi: 10.1016/0148-9062(93)90041-B   
31. Mansurov VA. Acoustic emission from failing rock behaviour. Rock Mechanics and Rock Engineering. 1994; 27 (3): 173-182. doi: 10.1007/BF01020309   
32. Knill JL, Franklin JA, Malone AW. A study of acoustic emission from stressed rock. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. 2000; 5(1): 87-88. doi: 10.1016/0148- 9062(68)90025-9   
33. Cox SJD, Meredith PG. Microcrack formation and material softening in rock measured by monitoring acoustic emissions. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. 1993; 30 (1): 11-24. doi: 10.1016/0148-9062(93)90172-A   
34. Wu LX, Wang JZ. Infrared radiation features of coal and rocks under loading. International Journal of Rock Mechanics and Mining Sciences. 1998; 35(7): 969-976.   
35. Petukhov IM, Linkov AM. The theory of post-failure deformations and the problem of stability in rock mechanics. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. 1979; 16 (5): 57-76. doi: 10.1016/0148-9062(79)91444-X   
36. Zhao ZH, Wang WM, Wang LH, et al. Compression-shear strength criterion of coal-rock combination model considering interface effect. Tunnelling and Underground Space Technology. 2015; 47: 193-199. doi: 10.1016/j.tust.2015.01.007   
37. Xue DJ, Zhou HW, Liu Jd. et al. Numerical simulation of stress wave propagation in coal-rock combination media. Advanced Materials Research. 2012; 594-597: 542-551. doi: 10.4028/www.scientific.net/AMR.594-597.542   
38. Tan YL, Guo WY, Gu QH, et al. Research on the rock burst tendency and AE characteristics of inhomogeneous coal-rock combination bodies. Shock and Vibration. 2016; 2: 1-11. doi: 10.1155/2016/9271434