Research Article
Hamiltonian Monte Carlo Method on Superstatistics of Stochastic Processes
1Department of Mathematics, University of Leicester, University Road, Leicester, United Kingdom
2Department of Mathematics, Umm Al-Qura University, Al-Qunfudah University College, Saudi Arabia
*Corresponding author: Omar Alzeley, Department of Mathematics, University of Leicester, University Road, Leicester LE1 7RH, United Kingdom, E-mail: oaia1@Leicester.ac.uk
Received: March 3, 2019 Accepted: April 26, 2019 Published: May 6, 2019
Citation: Alzeley O. Hamiltonian Monte Carlo Method on Superstatistics of Stochastic Processes. Madridge J Bioinform Syst Biol. 2019; 1(2): 40-43. doi: 10.18689/mjbsb-1000108
Copyright: © 2019 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Superstatistics is said to be a superposition contained in two different statistics relevant to those non-equilibrium systems that contain intensive parameters fluctuations and a stationary state. In most cases when dealing with superstatistics, we usually mean those non-equilibrium systems that contain complex dynamics. Some considered quantities include chemical potential, temperature or energy dissipation which is usually measured on a large scale. The measurement of the above quantities will depend on different statistical properties portrayed by them. The results obtained according to the fluctuation shown can be mechanical descriptions that are different according to elective statistics. The purpose of this paper is to investigate superstatistics of type B as well as to generalise this type when the density distribution is unknown. Hamiltonian Monte Carlo has been applied to cover the problem of unknown distribution or not easy to sample from.
Keywords: Superstatistics; HMC; Metropolis-Hastings algorithm; Bayesian theory.
Introduction
Ordinary statistical mechanics, due to given underlying reasons, may not be applicable to some particular systems. Some of these reasons can include metastability, some driving forces that can keep the system out of equilibrium and so on [1]. In studying a larger number of physical systems, Tsallis distributions are frequently observed. Many of the observations made are found in the driven stationary state that is usually far from equilibrium. According to Beck [1], a significant question is why these or similar distributions are frequently observed in experiments. Furthermore, another point of concern is whether we can be in a position to give a dynamic reason as to why Tsallis statistics occurrence is not a suitable class of nonequilibrium systems. The occurrence is possible. It is possible for an individual to come up with a class of stochastic differential equations that have fluctuating parameters, the process can rigorously prove can generate Tsallis statistics [2]. Tsallis distributions in many systems are observed for the simple reason that they can easily be associated with the presence of spatiotemporal fluctuations of an intensive parameter. They include, the amplitude of the Gaussian white noise, friction constant, inverse temperature, or energy dissipation in turbulent flows. Tsallis statistics naturally end in case where these fluctuations evolve over a long time and are distributed in regard to a particular distribution, the χ2-distribution. For other distributions made up of intensive parameter, in most cases, one obtains general statistics. However, when Tsallis statistics are contained in the so-called superstatistics, they can be regarded as a special case. Generalized entropies (294 C. Beck analogues of the Tsallis entropies) can be defined as related to these superstatistics from the principle, it is also possible that the generalised versions of statistical mechanics can be constructed from the above assumption. It has been indicated that the correspondents of generalised entropies are generally stable [3]. In this paper, we will have to look into insights about the superstatistics concept, and also investigate superstatistics type B via the Bayesian approach. We also address a problem that is of great interest in experimental applications. Given a probability density, how can we check and determine the conjugate priori distribution? The outline of this paper is as follows: in the next section, we discuss and review superstatistics. In Markov Chain Monte Carlo for Superstatistics section, we introduce and formulate the problem of interest of this paper, and in Hamiltonian Monte Carlo sampling for Superstatistics section, we investigate and review a powerful technique called Hamiltonian Monte Carlo sampling. We conclude our paper in Conclusion section.
Superstatistics of Type B and Bayesian Theory
If the conditional probability is p(u|θ), then the probability is obtained. Where the probability of u is given some value of θ;
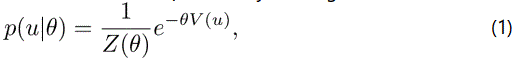
in the case of joint probability p(u, θ), the probability used in observing certain values of u and also those of certain values of θ;

and on the case of marginal probability p(u), the probability that is used in observing certain values of u and also those of certain values of θ;
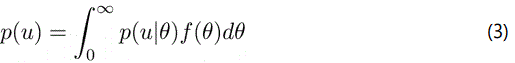
Generalisation of the canonical distribution of the superstatistics is considered a marginal distribution. The formulas proposed above are related to type B superstatistics, which is the subject of this paper. Our purpose is to find this kind of marginal probability by using Bayesian theory. To investigate this, we review some important concepts in Bayesian Theory, which allow us to compute the posterior distribution of any distribution of interest. Using Bayeʼs theorem, we can calculate the posterior probability density function of θ:

where, m(x)=∫px(x|θ)π(θ)dθ. The conjugate prior gives rise to posterior distribution of the same form as the prior. It is notable that the conjugate family may exist even if px(x|θ) is not in the exponential family moreover, the conjugate prior make calculation of the posterior easier. To illustrate how Bayesian approach can be used to compute superstatistics type B, we consider some examples taken from the study of superstatistics by Briggs [4], which can be generalised to any superstatistics in similar situations.
Example 1.
The Poisson process has been used for the study of modeling train delay [4]. The Poisson process is given by p(t|β)=βe-βt. The conjugate prior of Poisson is Gamma, which is given by
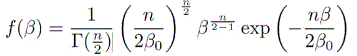
Using eqn (4) or instead using π(θ|x) ∝ px(x|θ)π(θ) gives the following
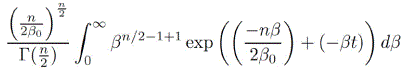
This will give 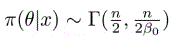 . Therefore, one can show that this result led to q−exponential distribution so the marginal distribution
. Therefore, one can show that this result led to q−exponential distribution so the marginal distribution 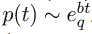 . Another example we consider in this paper is Gaussian.
. Another example we consider in this paper is Gaussian.
Example 2.
The Gaussian process is given by
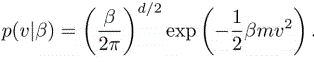
The conjugate prior distribution of Gaussian with known mean is inverse gamma, which is given by
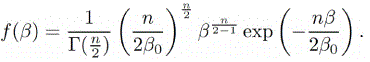
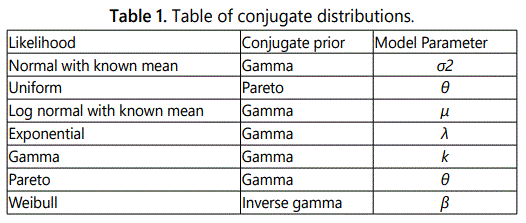
Similarly, by using eqn (2) and following the same procedure as the previous example we obtained 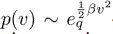 . This method can be used when we know the conjugate prior as well as the marginal likelihood. Table 1 illustrates conjugate distribution of some well-known probability distributions. In Hamiltonian Monte Carlo sampling for Superstatistics section, we show some method for finding the posterior when it is not easy to sample.
. This method can be used when we know the conjugate prior as well as the marginal likelihood. Table 1 illustrates conjugate distribution of some well-known probability distributions. In Hamiltonian Monte Carlo sampling for Superstatistics section, we show some method for finding the posterior when it is not easy to sample.
Markov Chain Monte Carlo for Superstatistics
In this part, we applied the Markov Chain Monte Carlo method to super-statistics. To the best of our knowledge this method has not previously been applied to superstatistics theory. The aim of our claim is to generalised su- perstatistics to type B when the conditional probability is unknown. If the conditional probability in Superstatistics of type B and Bayesian theory section is obtained where the probability of u is given some value of θ, as in eqn (1). Then the probability that is used in observing certain values of u and those of θ is given by eqn (2). The marginal probability is given by
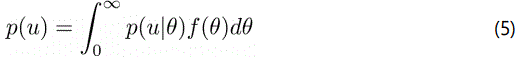
Generalisation of the canonical distribution of superstatistics is considered a marginal distribution. The formulas proposed above are related to type B superstatistics, which is the main topic of this paper. Our purpose is to find this kind marginal probability by using Bayesian theory or Bayeʼs theorem (eqn (4)). The conjugate prior gives rise to a posterior distribution of the same form as the prior. It is notable that the conjugate family may exist even if px(x|θ) is not in the exponential family moreover, the conjugate prior makes calculation of the posterior easier. To illustrate how the Bayesian approach can be used to compute superstatistics type B, we consider some examples taken from the study of superstatistics by Beck [2], which can be generalised to any superstatistics in a similar way.
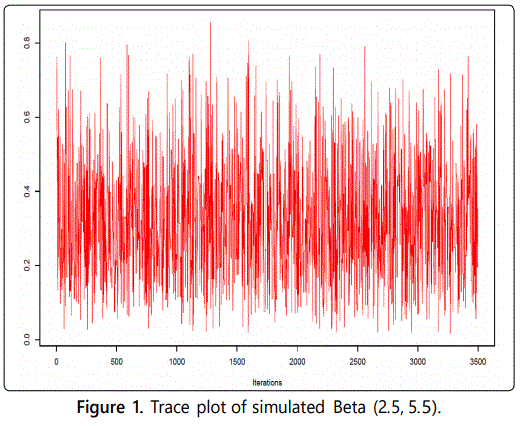
Example 1. Uniform distribution. We test uniformity by using MCMC. The algorithm we used here is Metropolis Hastings algorithm (see [5] for more details of its description). The proposal distribution is uniform and the target distribution is Beta with mean 2.5 and variance 5.5. We compare the theoretical mean and variance of Beta distribution with simulation output as shown in the table below.

We further investigated the simulation result by conducting a hypothesis test using Kolmogorov Smirnovʼs test of equality between the two samples. The test result was D=0.022286, p-value=0.3497. This means that both samples are compatible, with the same distribution.
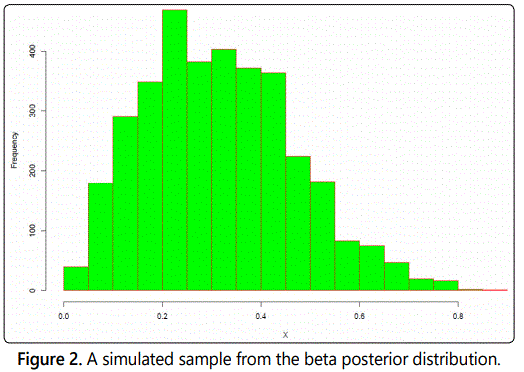
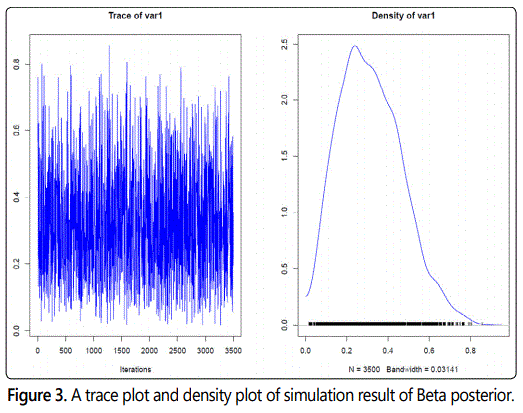
Hamiltonian Monte Carlo sampling for Superstatistics
The Hamilton Monte Carlo (HMC) algorithm is an example of the various sampling forms of the Markov Chain Monte Carlo (MCMC) algorithm, as it mainly entails the use of Hamilton evolution [6,7]. This evolution can be significantly explained by the use of a particle which is left to freely slide over a smooth surface with varying heights. In such a case, the potential energy of the particle at its current position is directly proportional to the height of the sliding surface. Hence the kinetic energy (KE) is given by Chaudhuri et al. [6], 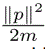 , where p is the particles momentum vector at its current position, and m is its mass. As the particle moves up and down through the smooth surface, significant changes are recorded in its kinetic energy. Despite the changes in the total energy, which is the total sum of the kinetic and potential energy, energy incurred is still conserved. For this reason, in cases where the particle moves through an un-expected inclining slope, it is able to maintain its initial motion to a position when its kinetic energy reduces to zero, before sliding backwards. Using HMC sampling: Let θ be the particleʼs current position. The kinetic and potential energy of the particle at this position would become:
, where p is the particles momentum vector at its current position, and m is its mass. As the particle moves up and down through the smooth surface, significant changes are recorded in its kinetic energy. Despite the changes in the total energy, which is the total sum of the kinetic and potential energy, energy incurred is still conserved. For this reason, in cases where the particle moves through an un-expected inclining slope, it is able to maintain its initial motion to a position when its kinetic energy reduces to zero, before sliding backwards. Using HMC sampling: Let θ be the particleʼs current position. The kinetic and potential energy of the particle at this position would become:
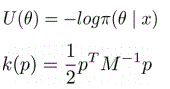
From these equations, artificial construction of the particles momentum vector is assumed to be p=(p1,…, pd)T, while the mass matrix M, becomes the symmetric positive definitive matrix. From this, the kinetic energy incurred is taken from a point N(0, M). M, in this case, may be assumed to be equal to mI, which is the mass of the particle. Therefore, from Hamiltons equation, the total energy would become [6]:

However, since the total energy incurred from this system is usually conserved, from Hamiltons equation, the derivatives of position θ of the particle and its momentum p over a given time t gives the new equation of motion as
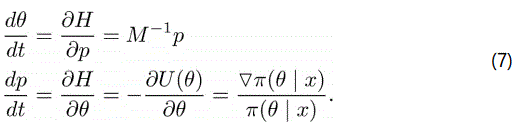
Generally, Hamilton dynamics are constant; they can be reversed and, at the same time, preserve their volume, making them fit for MCMC sampling. For this reason, no analytical solutions exist from the differential equation (7) above, since no analytical form exists for π(θ|x) either. Similarly, from Birdsall and Langdon [8], applying the leapfrog integration method in Hamiltonʼs equation, the time variable t is replaced by δ, and the current position p is replaced by θ, hence denoted as θ(t) and p(t) respectively. Thereafter, the position and momentum equations at point t+δ are given as [6]
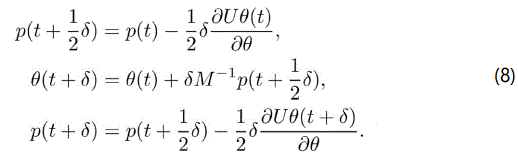
The general importance of the leapfrog integration method is that it maintains the reversible property of Hamiltonʼs equation due to its symmetry while, at the same time, maintaining the exact volume. However, the Hamiltonʼs property of being continuously constant is lost due to the various approximations introduced that cause several errors, which then lead to it being rejected.
Moreover, the MCMC algorithm also makes room for an accept-reject step that guarantees correct order of the samples, which entails significant limits, as clearly depicted in the Langevin-Hastings algorithm, described by Leimkuhler and Reich [9]. According to Leimkuhler and Reich [9], new values of momentum vector p are randomly picked from the N (0, M) distribution, at the beginning of the HMC iteration. These Hamilton dynamics are then duplicated for T steps using the leapfrog method in equation (6) above, with (θ, p) as the current state. In the end, at the final state (θ*, p*) of the T-step trajectory, the most accepted equation could then be written as
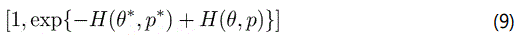
Discussion and Conclusion
In the recent past, research about superstatistics has been undertaken to ensure that several discoveries have been made. Applications are being undertaken to explore that all the possible areas superstatistics can be used in make sure that the analysis of different quantities can be undertaken without any problem. Areas like statistics of cosmic rays, chaotic defect motion in inclined layer convection and fully developed hydrodynamic turbulence have been used to ensure that superstatistics has developed well. This is an indication that different scholars have been working to maintain intense innovation that will make superstatistics a better field to study. Apart from the discoveries, there are some areas that have been not been developed well to ensure that superstatistics are commonly understood. Several discoveries should be made in a bid to ascertain that all the potential areas are explored. Therefore, scholars are required to continually find new areas where superstatistics will be used, which could facilitate progress in the analysis of different quantities such as biology.
In summary, there has been consideration of generalised statistics, referred to as superstatistics. Conversely, Tsallis statistics in the setting is a special case found in superstatistics. The dynamical parameter q is also another class that can be used in defining all the new statistics. There has been an indication on how small variance of the fluctuations behaves in the case of universal superstatistics. When there is a large variance, there exists a difference in the information provided about the underlying complex dynamics. Where there are complex nonequilibrium problems, there might be a requirement for different types of superstatistics. Tsallis statistics is one of the examples of many possible new statistics that may exist. The measurement of the above quantities will depend on different statistical properties portrayed by them. The results obtained according to the fluctuation shown can be mechanical descriptions that are different according to elective statistics. Therefore, from the principle, it is also possible that the generalised versions of statistical mechanics can be constructed from the above assumption. It has been indicated that the generalised entropies, correspondents are generally stable. The usefulness of Hamiltonian dynamics is converting the density function for sampled distribution to a potential energy function, as well as introducing momentum variables to go with the original variables of interest. This allows us to simulate a Markov chain in which each iteration resamples the momentum, as well as a Metropolis update with a proposal found using Hamiltonian dynamics.
References
- Beck C. Superstatistics: theory and applications. Continuum Mech Thermodyn. 2004; 16(3): 293-304. doi: 10.1007/s00161-003-0145-1
- Wilk G, W~lodarczyk Z. Interpretation of the nonextensivity parameter q in some applications of tsallis statistics and l´evy distributions. Phys Rev Lett. 2000; 84(13): 2770-2773. doi: 10.1103/PhysRevLett.84.2770
- Briggs K, Beck C. Modelling train delays with q-exponential functions. Physica A. 2007; 378(2): 498-504. doi: 10.1016/j.physa.2006.11.084
- Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys. 1953; 21(6): 1087-1092. doi: 10.1063/1.1699114
- Chaudhuri S, Mondal D, Yin T. Hamiltonian Monte Carlo sampling in bayesian empirical likelihood computation. Journal of the Royal Statistical Society: Series B (Statistical Methodology). 2017; 79(1): 293-320. doi: 10.1111/rssb.12164
- Neal RM. MCMC using hamiltonian dynamics. In: Brooks S, Gelman A, Jones G, Meng XL (eds). Handbook of Markov Chain Monte Carlo. 2011:113-162.
- Birdsall CK, Langdon AB. Plasma physics via computer simulation. CRC press. 2004. 504.
- Leimkuhler B, Reich S. Simulating hamiltonian dynamics. Cambridge University Press. 2005: 14. doi: 10.1017/CBO9780511614118


