Abstract

The invention of composite solid propellants enabled close packing of fuel and oxidizer particles, leading to modern propellants. The superior mechanical properties of the polymer matrix allowed more propellant to be placed in a rocket motor pressure vessel through case bonding (bonding propellant directly to the vessel case). Propellants are often stored for periods of up to 20 to 40 years during which time they can degrade under the action of environmental conditions. This may eventually be manifested through formation of surface cracks. Degradation over time, or aging, is therefore important.

Aging is a complex mechanical and chemical process, involving multi-scale, multi-disciplinary mechanisms, from atomic, molecular scale to micro- and macro-scale events. Many of its intimate details are poorly understood, making aging prediction a challenge. Our research has shown that a mechanical property, tangent modulus, is a key aging indicator. Data base analysis showed a connection with strain rate, ambient storage time, gel fraction of the matrix polymer, matrix cross link density, molecular weight of the polymer sol, and propellant density may exist. A dimensionless ratio containing these parameters was formed to predict propellant failure. Statistical analysis showed that HTPB iodine number and normalized absorbance also correlate with tangent modulus.

Keywords: Structural capability, propellants, Ambient tangent modulus

Nomenclature

C : Structural capability
ε : Strain, in/in
ε^. : Strain rate, in/in/min
E : modulus, lb/in²
f : fractional amount
FS : factor of safety
K : knock down factor
L : load, lb
M : molecular weight, grams/mole
ρ : density, lb/in³
S : safety factor
σ : stress, lb/in²
t : ambient storage time, weeks
Subscripts
Gel : polymer gel component
m : maximum
n : normalized
sol : polymer sol component
t : tangent
x-link : polymer intra chain cross links

Introduction

The need for new propellants is accelerating, prompted by the new space age, US-Russian-Chinese arms race, and hypersonic flights [1-3]. Nations of the world have announced new planetary explorations aimed at reaching deeper and further into space [4-7]. This will require high performance propellants. As hypersonic missiles begin to emerge, an arms race is inevitable and new propulsion technology is needed for both offense and defense against this new capability.Nations will therefore strive to acquire robust missile defense capability [8-12]. Solid propellants will be increasingly harnessed for commercial access to earth orbit and beyond. In that application, safer and more environmentally friendly formulations will be needed whilst at the same time satisfying the desire for higher performance [13]. The need for new propellants is rising. They must not only be more energetic but must also be able to withstand environmental rigors during storage for long periods of time.

The current solid composite propellants consist of solid fuel and oxidizer particles, usually aluminum and ammonium perchlorate, respectively, suspended in a polymeric matrix or binder, as shown in Figure 1. To achieve maximum energy output, filler particles over a range of sizes are used to achieve the highest packing density. The largest particle size used is about 250 μm.

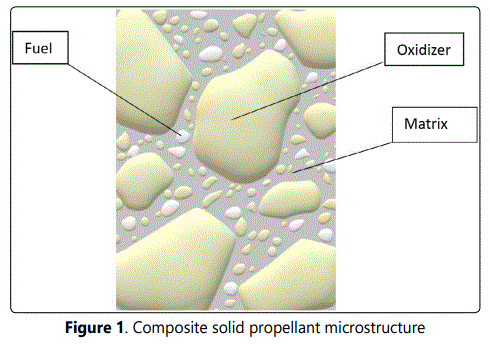
Solid composite propellants release energy at a controlled rate, burning only on exposed surfaces. The combustion gases that are produced pressurize the rocket motor vessel. They vent through a nozzle to generate thrust. Propellant is consumed on the regressing solid surface until the entire mass is gone. The charge, or grain, combustion gas production rate is therefore controlled by the total exposed surface area throughout burning. This may or may not be constant depending on the needs of the mission. Grain geometry determines the burning surface area history. If the grains have surface cracks, the combustion process may be disrupted when burning ensues on the exposed crack faces [14-16].

Solid composite propellants are the culmination of years of formulation development that include earlier types, such as nitrocellulose and nitroglycerine double base [17]. Nitrocellulose is produced through nitration of cotton. Using the process developed to manufacture celluloid, it is plasticized with nitroglycerine. The resulting material can be cast into three dimensional grains and loaded into rocket pressure vessels. Double base propellants have high tensile modulus and low elongation, and the grains must be free standing. If they are bonded to their rocket motor chamber, cracking during fluctuation of ambient temperature is likely. HTPB composites have low modulus and high elongation over a wide temperature range and can be case bonded without risk of fracture. Case bonding raised volumetric efficiency, paving the way to modern rocket motor designs [18]. These include the large solid boosters that were used on the Space Shuttle [19]. As a bonus, HTPB composite propellants have higher density than double base with an attendant higher energy per unit volume. The mechanical properties of the former can, however, change over time under environmental aging. Gui-Yang Li and Celina noted oxidation of the polymers commonly used as the matrix material [20, 21]. The propellant grains become weak over time, leading to lower structural integrity. Understanding all degradation mechanisms is therefore the key in predicting reliability of these class of propellants.

Solid propellant design and quality control has been an empirical trial and error process. In deploying the propellants, conservative guidelines are used to compensate for the lack of precise understanding of the degradation mechanisms. Various propellant formulations and batches have been analyzed to get dependable batch-wise material data for failure prediction models [22].

Quantifying Structural Integrity

Composite solid propellants are, by virtue of their polymer matrix, visco-elastic [23]. Extensive tensile testing is required to characterize mechanical properties. In some cases, accelerated aging experimental results are used to forecast long term degradation at ambient temperature. Propellants mechanical properties can be tracked over time by comparison to baseline data [24]. Linear approximations are frequently used to describe the polymer matrix viscoelastic behavior (sometimes non-linear). Time-temperature superposition is used to estimate the moduli, strength, and elongation under transient loading conditions [25-27]. In this way mechanical properties corresponding to conditions not easily measured directly, such as ignition pressurization or long-term storage, can be readily estimated. Factor of Safety is commonly used to compare propellant structural integrity to load:

FS=(CK)/(LS) (Ref. [28]) (1)

Structural capacity, C, is the maximum stress or strain, as appropriate. Load, L, is the applied force or strain, as appropriate. Knock down factors, K, allow for material property variation including material property degradation variations due to aging. Typical values are in the 0.75 to 0.80 range. Amid all these experienced-based correlational factors, the last approximation is the linear model of viscoelastic behavior and other undefined factors. These are included in the safety factor, S, which ranges from 1.25 to 1.50. So, Equation 1 used in this way, represents 2 to 3 times safety margin. For new formulations or those with less experience, higher safety factor values within this range are frequently used.

In this kind of empirical design model, there are many uncertainties. To increase confidence in the model the worstcase load limit is occasionally verified by placing the rocket motor through a “temperature conditioning” sequence in a temperature-controlled chamber. Set to the lowest storage limit temperatures, typically from -20°F to -40°F the propellant is allowed to come to thermal equilibrium. The propellant is then examined, e.g., by x-ray, to observe any damage the grain may have sustained. Full scale tests like these are used to cross-check the model. The test is carried out at the discretion of the test engineer if the material is new, or the experience data base is insufficient.

The factor of safety is a historical model that has been used. While it works, it also masks the lack of fundamental insight and understanding of how each parameter influences one another to reach an outcome. This leads to consistent and significant over-design. Knock down and safety factor values are system specific and may not be applicable to systems outside of the data base and therefore do not apply to new designs.

Current Solid Propellant Aging Models

The numerous degradation phenomena governing composite solid propellant aging have spawned a multitude of predictive models. Given the large role structural strength of the propellant plays many models focus on predictions of mechanical property changes over time. Periodic sampling of propellant samples stored at ambient temperature is the most straight forward way to determine how quickly this takes place. This of course takes time and is not too practical if the goal is predicting the fate of a large population of rocket motors in advance. One driving force behind change is chemical reactions, i.e., polymer oxidation. That reaction rates increase as temperature rises can be used to advantage to characterize changes more quickly. Propellant samples are therefore commonly stored at one or more (three is common to test for linearity) above ambient temperatures and periodically tested. The results are frequently analyzed using the well-known Arrhenius equation [24,29,30]. Plots of mechanical property change rate versus reciprocal absolute temperature are extrapolated to predict how quickly changes occur at ambient storage conditions. This has the advantage of arriving at a result in a smaller period than would be the case if only ambient temperature storage and testing were performed. Arrhenius modeling of empirically measured mechanical properties avoids the more complex problem of delving into the chemical kinetic details that underpin the changes being observed. The procedure is, however, not without pitfalls. It is now known that even in the case of the most elementary chemical reactions that the Arrhenius equation is not strictly obeyed [31]. Curvature in its characteristic reaction rate versus reciprocal temperature curves is often observed making extrapolation of acceleration data back to ambient risky [32]. Furthermore, propellant oxidation may be limited by oxygen diffusion rate through the polymer matrix, adding further modeling complication [33, 34]. To overcome these limitations a kinetic mechanistic model of solid phase polybutadiene oxidation has been conceived [35]. Through direct modeling of atomistic changes in the polymer matrix it may be possible to predict corresponding macro scale mechanical properties, although not without additional modeling challenges [36-39].

Structural damage and other changes arising from stress and strain imposed on the propellant also can alter mechanical behavior over time. This aspect involves the polymer matrix and its adhesion to the filler particles (above 80% by weight filled is common). Fatigue damage is manifested as internal matrix tears and adhesion failure between polymer and filler particles, the latter process referred to as dewetting [40]. Damage is often quantified using the linear rule developed by Miner (an increment of damage is defined as the ratio of the time a constant stress is applied to the time needed for it to cause fracture. Increments are additive, even if produced at different stress levels). Although this simple approach is at best an approximation of a more complex process it is still commonly used for lack of community agreement on anything else [41]. Study of the damage process continues to be an area of active research [42-45].

Filled polymers often exhibit non-linear stress-strain loading curves with hysteresis. The latter phenomenon is the well-known Mullins effect [46-59]. When loaded and then reloaded, stress is lower than what was observed in the first extension, up to the maximum strain of the prior load, a phenomenon called stress softening. Furthermore, the polymer does not recover all the strain that was applied but takes a “permanent set” in its unloaded state [60-62]. This phenomenon can slow the accumulation of damage by reducing applied stress during subsequent loading. Damage and Mullins effect phenomena are observed in all composite propellants that employ polymer matrices. They impact the magnitude of stress and hence bear on how prevalent cracking and other structural failure, such as propellant to case bond release.

We therefore see that composite solid propellant degradation and aging is characterized by numerous competing phenomena. They have been singularly and collectively incorporated into models to forecast when failure occurs. Oxidation and hydrolysis, for example, have been used as the sole criterion [29]. Length of time needed for propellant tensile modulus to move outside of its designer prescribed limits under the action of these phenomena was taken to be end of life. Alternately, a 30% decrease in maximum elongation has been used as an end-of-life criterion [63]. Christiansen modeled aging changes in physical and mechanical properties over time as the ratio of the current value to its initial value proportional to the logarithm of time [64]. Fatigue damage arising during periodic loading lowers solid propellant strength. Heller combined this effect with aging to conceive a model in which end of life occurs when damage degraded strength falls below applied stress [65]. His model is posed probabilistically to account for the often-large variability in propellant mechanical properties and load magnitude typically encountered. Storage, shipping, and deployment temperatures during the often-complex logistic sequence can vary from one rocket to another. Corresponding variation in mechanical stress from thermal contraction and expansion therefore occurs. Within and between propellant batches mechanical property variation can also be significant. All of these sources of variability easily cause damage fluctuation between individual rockets in a given population to range over orders of magnitude. The algorithm, A Global Engineering Model of Damage (AGEMOD), also accounts for variability, using a Monte Carlo simulation encompassing both mechanical properties and load history [66, 67]. End of life is declared when the fraction of simulations in which cumulative damage sufficient for propellant cracking becomes excessively high. AGEMOD accounts for both chemical aging and permanent set using empirical data. Both Heller’s and Biggs’ models use Miner’s damage rule.

In summary, we see that solid propellant mechanical properties are governed by an array of complex phenomena. Robust physics, mechanical, and chemical based models for each of them remain elusive. In their absence empirical methods are commonly used. Attempts to model their interaction to predict propellant aging failure therefore likely entails error. We will provide an expanded discussion of these models in a separate paper to be published in the future. An alternate approach to discrete phenomena modeling may offer an alternate path with potential to quickly advance the science. Dimensional analysis is one such method.

Parameter Dimensionless Ratios: A Potential Path to a Universal Model

Certain parameters may play an especially strong role in composite solid propellant behavior. When they are judiciously combined it may be possible to create a single model of this entire material class. We selected tangent modulus to illustrate this process, owing to its key structural integrity role. Tangent modulus is the slope of the stress versus strain curve, Figure 2. As shown, it is the ratio of change in stress over corresponding change in strain,

E_t = (σ₂ – σ₁)/ (ε₂ – ε₁) (2)

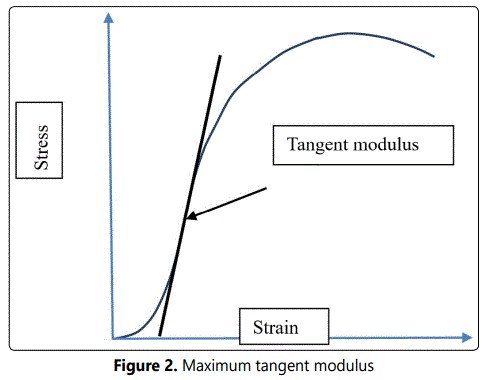
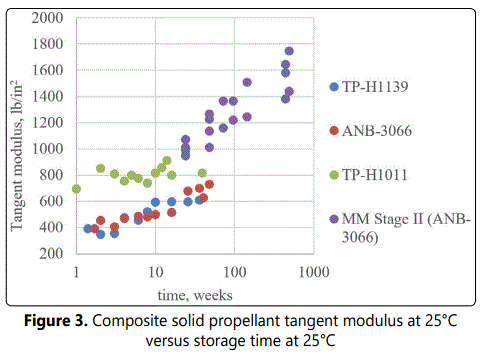
Grain stress is directly proportional to modulus under application of load. Modulus therefore has direct bearing on the onset of grain fracture, playing a central structural integrity role. Increasing tangent modulus, over time, of HTPB matrix solid composite propellants is observed in a group of four formulations, Figure 3 [22, 68-70]. Although all exhibit increasing modulus over time, they do not share a common intercept.

Osbourne Reynolds used a dimensionless system parameter ratio to gain insight on material behavior [71]. The Reynolds Number, a ratio of inertial to viscous forces, reveals when transitions from laminar to turbulent fluid flow occur. This approach was used to see if a universal tangent modulus relation could be found.

A dimensionless ratio incorporating matrix material physical property and loading parameters was constructed. Those selected are either observed or suspected of having some correlation with tangent modulus. Strain rate, ambient storage time, the weight fraction of the matrix polymer that is in a gel state, the matrix polymer cross link density, the molecular weight of the matrix polymer sol fraction, and solid propellant density were selected. Parameters that are expected to increase modulus appear in the ratio numerator. In accord with the visco-elastic nature of composite solid propellant, increases in ε^. lead to higher modulus. Increases in gel fraction and cross link density signal a greater degree of matrix interconnection, also raising modulus. As the molecular weight of the matrix sol fraction goes up, the increase in size of these free-floating molecular species should inhibit viscos flow of the matrix. This too should increase modulus. Increasing density is also associated with rising modulus, reflecting the higher concentrations of polymer chain cross links as oxidation proceeds and the addition of oxygen atoms to the chains. Despite this it was placed in the denominator, as a means of preserving the dimensionless nature of the ratio. Density rises slowly, however, only about 0.09% over forty years [22]. Gel fraction, in comparison, rises as much as 13% in over just thirty-five weeks [68]. This dwarfs the impact of density whose role is to play only a small moderating influence, in this application, on how quickly tangent modulus rises over time. Sol fraction, i.e., 1 – f_gel, is placed in the denominator since greater proportions of polymer sol lower modulus, owing to reduced level of matrix interconnection it represents. Using these criteria, the ratio is:

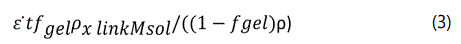
Application of this expression, Figure 4, reveals a continuous single function that can be used to predict ambient tangent modulus, independent of propellant formulation.

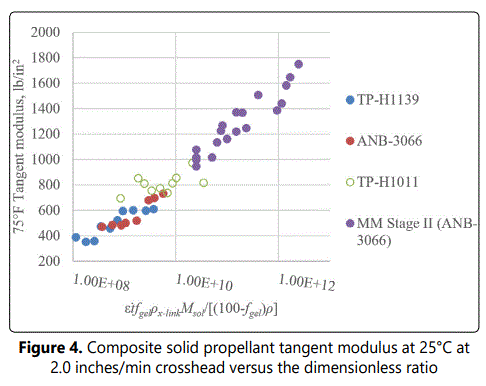
This example is illustrative owing to a lack of measured values for some of the ratio parameters from every formulation. Where specific values were not available, generic ones, typical of composite solid propellants, were used. For some (propellant density and cross link density) the same value was used for each formulation. M_sol was arbitrarily varied, within the range of typical values, to yield the Fig. 4 smooth curve. Two different values were used across the four formulations, and these were not varied over time. It is possible that M_sol could increase with time as oxidation serves to connect individual sol molecules to themselves, prior to their incorporation into the gel matrix, but its consideration was beyond the scope of this analysis. Crosslink density was also held constant over time. Although this is not realistic (crosslink density should increase as oxidation proceeds) it was mathematically simpler than manipulating it, along with Msol. The result would be the same. All the tests analyzed were run at a common strain rate, therefore the role of extension speed was not directly tested. However, the strong dependence of tangent modulus on strain rate is widely known. Values of parameters held constant over time are summarized in Table I. Gel fraction and density was varied over time based on the published data. Despite the noted simplifications and assumptions, this example shows excellent potential for a multi formulation tangent modulus model, or in other words, the range of each of the parameter values is large enough to easily allow for the possibility of the universal dimensionless ratio proposed here. Measurement of all the ratio parameters on all the formulations over time is needed to conclusively prove this approach is valid. The next phase of analysis sought to see if additional parameters having correlation with tangent modulus exist. A purely statistical approach was used to see if this might be the case.

A Statistical Approach to Uncover Tangent Modulus Parameters

As the dimensionless ratio example shows, universal fundamental parameter relationships, describing behavior of solid propellant as a material class may exist. In this case the parameters were selected based on their known influence on stiffness. There may be, however, additional parameters whose influence is less obvious but may nevertheless play just as important a role. A purely statistical approach was taken to see if this is the case. The largest number of available parameters having some correlation with tangent modulus was assembled towards this goal.

Twenty-two parameters, Table 2, were analyzed of which 295 observations were made [22, 68-70, 72]. They derive from acceleration testing of pure HTPB, and the four solid propellant formulations shown in Figure 3. A group of physical and mechanical properties were observed after samples were stored at various temperatures for different periods of time. The 295 x 22 matrix these data form was subjected to statistical analysis using IBM SPSS Statistics version 24 software.

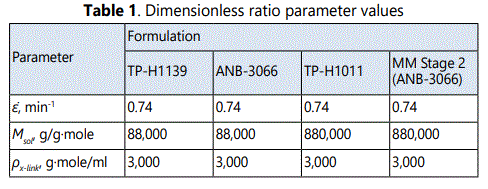
Statistical analysis ranked the parameters in order of importance for prediction of tangent modulus, Table 3. The strongest interdependence is between ambient and 125°F tangent modulus. Several influential intrinsic physical parameters also emerged. They include gel iodine number, normalized density, percent of the matrix in a gel state, HTPB normalized absorbance, and sol iodine number. In pursuit of a fundamental basic model, analysis focused on the first four of the latter group (highlighted in Table 3). Iodine number was included only once.

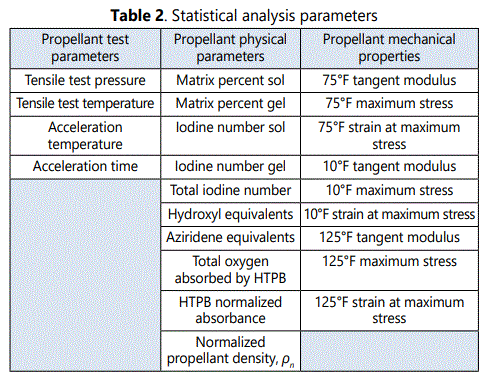
The physical parameters (shown in Table 3) were used to perform regression analysis for tangent modulus, as shown in Figure 5. The model has high correlation with its respective dependent variable, with R2 of 0.738. Iodine number is the most important physical correlation parameter. Iodine readily reacts with carbon-to-carbon double bond species. Thus, there appears to be a direct link to oxidation, a process that reduces the number of these chemical species on the HTPB polymer backbone over time.

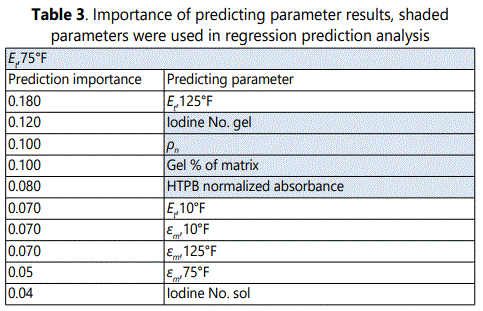
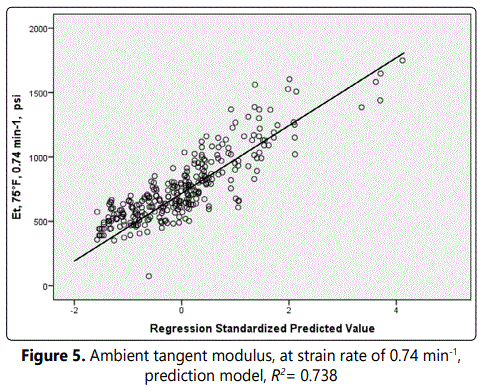
Gel fraction and density, parameters that were included in the dimensionless ratio, appeared again. Finding that polymer double bond population also plays a role illustrated that a statistical approach could identify latent parameters that might otherwise have been overlooked. Dependence of tangent modulus on double bond population size is therefore a significant finding, as was normalized absorbance, which also emerged in the analysis.

Discussion

The dimensionless ratio and SPSS statistical analysis of ambient tangent modulus suggest that a universal predictive model may exist. Reliance on formulation specific macroscopic empirical data, i.e., mechanical property, could therefore be reduced and eliminated. Universal algorithms can also guide development of new propellant formulations by giving insight on what target values of physical parameters to set to get a desired tangent modulus or other key macro scale parameter.

More sophisticated statistical tools can provide means to identify the most important parameters from these propellant parameter data bases. Multi-variate analysis provides a means to study sets of simultaneous measurements on large groups of variables [73]. Cluster analysis is an exploratory technique to find subsets of related parameters [74, 75]. Each observation in a multivariate data set, consisting of individual values of each system parameter, is taken as a point in multidimensional space [76]. Items (observations), in addition to variables, often segregate into natural groupings. This may provide new insight into the data. Cluster analysis is therefore a good place to begin investigation of solid composite propellant, whose groupings are unknown currently.

Distance between observational points in multidimensional space can be used to reveal how many groups there are. The familiar square root of sum of the squares Euclidian distance is frequently the distance criterion used. Others exist. Subject matter knowledge can be used to identify the most useful groups, just as it was instrumental in building the tangent modulus dimensionless ratio. Variables are grouped according to correlation coefficient or some similar measure. The number of groups for any meaningful collection of observations and variables is extremely high. It is not practical to examine each one, even with high-speed computers. Algorithms are commonly used to search for the most promising groupings [77, 78].

Several clustering algorithms are commonly used, such as hierarchical methods [79, 80]. To begin, each observation is taken to be an individual cluster. The two closest are then merged, becoming a new cluster. This process repeats until all the data become a single large cluster. Cluster hierarchies found during this process often yield insight into the latent data structure. Nonhierarchical methods begin by either setting initial cluster seeds or randomly partitioning the items into groups [81]. The observations are then redistributed to different clusters, one at a time, using distance to the centroid (centroid is the desired outcome) of the nearest cluster as a criterion. Numerous analyses with different clustering algorithms and definitions of “distance” are often performed on a given data set. If the same clustering structure is consistently obtained there is more confidence the results are meaningful. Comparison of hierarchical and nonhierarchical methods is a topic of ongoing research [82-84].

Many observations on a diverse group of parameters will be indispensable in pursuit of a universal solid propellant aging model. This must significantly exceed the set examined here to ensure that a significant number of meaningful clusters are identified; and errors through omission of latent phenomena are minimized. Given the large role that the polymer matrix plays, through its susceptibility to degradation over time, analysis of an expanded number of parameters related to its structure may be fruitful. Expansion of the types of experimental techniques used, beyond those historically employed, to probe structure could provide a means to accomplish this.

Nuclear magnetic resonance, for example, has been used to measure cross link density [85]. Light scattering might provide a means to make large numbers of observations on this class of matrix structure details [86, 87]. Size exclusion chromatography and asymmetric flow field flow fractionation can also be used to probe molecular configuration [88]. Differential scanning calorimetry can be used to observe changes in thermal decomposition details as propellant ages [89-92]. This may in some way correlate with matrix molecular structure. More recently, laser-induced breakdown spectroscopy (LIBS) has been used to study solid propellant aging [93]. Neutrons can be used to reveal two- and three-dimensional structural details [94]. They readily pass-through iron but are attenuated by hydrogen and therefore may readily reveal matrix details of propellants contained within pressure vessels [95]. Neutron scattering has already been used to reveal polymer structural details [96-100]. And, of course, FTIR was found useful in discerning oxidation product species and their spatial distribution within the propellant as found by the investigators cited earlier. All these experimental methods may yield the large parameter set needed to make a meaningful statistical analysis of composite solid propellants down to the micro scale. This may well lead to a substantial advance in the understanding of aging, yielding a robust predictive model. To begin, measurements of pure HTPB samples could be made with each candidate technique to see if any of them reflect changes taking place in the polymer over time. Those that do could be taken forward to testing with composite solid propellant.

Conclusions

Propellant aging is dominated by multiple complex phenomena: polymer matrix oxidation, Mullins effect, and fatigue damage to name a few. This is in large part because of the large role propellant strength plays. Modeling is phenomenological. Significant empiricism is therefore involved, and extensive laboratory testing is required each time a new propellant formulation is studied. End of life prediction models run the gamut of simply determining when a key mechanical property has changed by a threshold amount to models that attempt account for the interaction of the various phenomena involved and predict when propellant fracture occurs. In short, there is no consensus on approach.

Dimensional and statistical analysis offers a way to reduce the level of empiricism now required. It was shown that strain rate, ambient storage time, the gel fraction of the matrix polymer, the polymer cross link density, the molecular weight of the polymer matrix sol fraction, solid propellant density, HTPB iodine number and HTPB normalized absorbance each may play a role in the determination of tangent modulus across multiple formulations. A universal model that not only forecasts a key parameter but also predicts how it changes over time is therefore possible. This has potential to reduce the amount of laboratory characterization required for exercising all existing aging models.

Clustering statistical analysis may reveal even more relationships, beyond those identified in the tangent modulus example we studied. It could lead to a standalone universal predictive model. Measurement of an expanded number of parameters, with an emphasis on polymer matrix molecular structural detail is a potential path forward. End of life prediction from just the details of the formulation (ingredients, weight percentages, and particle size distribution) and its lifetime environmental exposure may be possible. The universal predictive tool that would follow would be a boon to rocket motor designers, eliminating much empirical developmental and scale up testing now performed.

References

1. Handberg R. The Future of the Space Industry, Private Enterprise and Public Policy. 1995.   
2. Nagendra NP, Basu P. Demystifying space business in India and issues for the development of a globally competitive private space industry. Space Policy. 2016; 36: 1-11. doi: 10.1016/j.spacepol.2016.02.006   
3. Apking AG. The Rush to Develop Space: The Role of Spacefaring Nations in Forging Environmental Standards for the Use of Celestial Bodies for Governmental and Private Interests. Journal of International Environmental Law & Policy. 2005; 16(2); 329-466.   
4. Morita Y, Imorita T, Imoto T, Habu H, Ohtsuka H, Hori K, Koreki T, Fukuchi A, Uekusa Y, Akiba R. Advanced Solid Rocket Launcher and Its Evolution. Transactions of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology. 2010; 8: 27. doi: 10.2322/tastj.8.Tg_19   
5. Surkov YA, Kremnev RS. Mars-96 mission: Mars exploration with the use of penetrators. Planetary and Space Science. 1998; 46(11-12): 1689-1696. doi: 10.1016/S0032-0633(98)00071-3   
6. Guery JF, Chang IS, Shimada T, Glick M, Boury D, Robert E, et al. Solid propulsion for space applications: An updated roadmap. Acta Astronautica. 2010; 66(1-2): 201-219. doi: 10.1016/j.actaastro.2009.05.028   
7. Boyle SA, Justiniano Yo-AV, Sisk MR. Bio-reduction of Solid Rocket Motors for Planetary Protection. Joint Army-Navy-NASA-Air Force In-Space Technical Interchange Meeting, Huntsville, AL. 2018.   
8. Kennedy WS, Kovacic SM, Rea EC, Lin TC. Solid Rocket Motor Development for Land-Based Intercontinental Ballistic Missiles. Journal of Spacecraft and Rockets. 1999; 36(6). doi: 10.2514/2.3508   
9. Lin TC. Development of U.S. Air Force Intercontinental Ballistic Missile Weapon Systems. Journal of Spacecraft and Rockets. 2003; 40(4). doi: 10.2514/2.3990   
10. Fabignon Y, Anthoine J, Davidenko D, Devillers R, Dupays J, Gueyffier D, et al. Recent Advances in Research on Solid Rocket Propulsion. Aerospace Lab. 2016; 11: 1-15. doi: 10.12762/2016.AL11-13   
11. Lipanov AM. Historical Survey of Solid-Propellant Rocket Development in Russia. Journal of Propulsion and Power. 2012; 19(6). doi: 10.2514/2.6945   
12. Naumann LW. Solid rocket propulsion for the German hfk (hyperschallflugkӧrper) hypervelocity missile program – an overview. 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. 2003; doi: 10.2514/6.2003-4969   
13. Davenas A. Future of Solid Rocket Propulsion. Solid Rocket Propulsion Technology. 1993; 585-602. doi: 10.1016/B978-0-08-040999-3.50019-9   
14. Lu Yue-Cherng, Kuo KK. Modeling and Numerical Simulation of Combustion Process inside a solid-propellant crack. Propellants, Explosives, Pyrotechnics. 1994; 19(5): 217-226. doi: 10.1002/prep.19940190502   
15. Godai T. Flame Propagation into the Crack of Solid-Propellant Grain. AIAA Journal. 1969; 8(7): 1322. doi: 10.2514/3.5892   
16. Kumar M, Kuo K. Ignition of Solid Propellant Crack Tip under Rapid Pressurization. AIAA Journal. 1980; 18(7). doi: 10.2514/3.50824   
17. Davenas A. Development of Modern Solid Propellants. Journal of Propulsion and Power. 2003; 19(6). doi: 10.2514/2.6947   
18. Caveny LH, Geisler RL, Ellis RA, Moore TL. Solid Rocket Enabling Technologies and Milestones in the United States. Journal of Propulsion and Power. 2003; 19(6). doi: 10.2514/2.6944   
19. Hunley JD. The History of Solid-Propellant Rocketry: What we do and do not know. AIAA 99-2925 Invited Paper at the 35th AIAA, ASME, SAE, ADEE Joint Propulsion Conference and Exhibit. 1999. doi: 10.2514/6.1999-2925   
20. Gui-Yang Li, Koenig JL. A Review of Rubber Oxidation. Rubber Chemistry and Technology. 2005; 78(2). doi: 10.5254/1.3547888   
21. Celina MC. Review of polymer oxidation and its relationship with materials performance and lifetime prediction. Polymer Degradation and Stability. 2013; 98(12): 2419-2429. doi: 10.1016/j.polymdegradstab.2013.06.024   
22. Aerojet Strategic Propulsion Co. Aging and Surveillance Program Minuteman II/III Stage II Program Progress. 1986; Report 0162-06-SAAS-38.   
23. Williams ML. Structural Analysis of Viscoelastic Materials. AIAA Journal. 1964; 2(5). doi: 10.2514/3.2447   
24. Judge MD. An Investigation of Composite Propellant Accelerated Ageing Mechanisms and Kinetics. Propellants, Explosives, Pyrotechnics. 2003; 28(3): 114-119. doi: 10.1002/prep.200390017   
25. Jeremic R. Some Aspects of Time-Temperature Superposition Principle Applied for Predicting Mechanical Properties of Solid Rocket Propellants. Propellants, Explosives, Pyrotechnics. 1999; 24(4): 221-223. doi: 10.1002/(SICI)1521-4087(199908)24:4<221::AID-PREP221>3.0.CO;2-U   
26. Seo WS, Kim JH. Estimation of Master Curves of Relaxation Modulus and Tensile Properties for Solid Propellant. Advanced Materials Research. 2013; 871: 247-252. doi: 10.4028/www.scientific.net/AMR.871.247   
27. Villar LD, Rezende LC. Time-Temperature Superposition Principle Applied to Thermally Aged Composite Propellant. 51st AIAA/SAE/ASEE Joint Propulsion Conference. 2015; doi: 10.2514/6.2015-4107   
28. Fitzgerald JE, Hufferd WL. Handbook for the Engineering Structural Analysis of Solid Propellants. Chemical Propulsion Information Agency. Accession Number: AD0887478, 1971.   
29. Adel WM, Liang G. Service life prediction of AP/Al/HTPB solid rocket propellant with consideration of softening aging behaviour. Chinese Journal of Aeronautics. 2019; 32(2): 361-368. doi:10.1016/j.cja.2018.08.003   
30. Villar LD, Cicaglioni T, Diniz MF, Takahashi MFK, Rezende LC. Thermal Aging of HTPB/IPDE-based Polyurethane as a Function of NCO/OH Ratio. Materials Research. 2011; 14(3): 372-375. doi: 10.1590/S1516-14392011005000063   
31. Logan SR. The Origin and Status of the Arrhenius Equation. Journal of Chemical Education. 1982; 59(4): 279-281. doi: 10.1021/ed059p279   
32. Celina M, Graham AC, Gillen KT, Assink RA, Minier LM. Thermal Degradation Studies of a Polyurethane Propellant Binder. Rubber Chemistry and Technology. 2000; 73(4): 678-693. doi: 10.5254/1.3547613   
33. Audouin L, Langlois V, Verdu J. Review, Role of oxygen diffusion in polymer ageing: kinetic and mechanical aspects. Journal of Materials Science. 1994; 29: 569-583. doi: 10.1007/BF00445968   
34. Moon B, Jun N, Park S, Seok CS, Hong US. A Study on the Modified Arrhenius Equation Using the Oxygen permeation Block Model of Crosslink Structure. Polymers. 2019; 11(1): 136. doi: 10.3390/polym11010136   
35. Coquillat M, Verdu J, Colin X, Audouin L, Neviere R. Thermal oxidation of polybutadiene. Part 2: Mechanistic and kinetic schemes for additive-free non-crosslinked polybutadiene. Polymer Degradation and Stability. 2007; 92(7): 1334-1342. doi: 10.1016/j.polymdegradstab.2007.03.019   
36. Seitz JT. The estimation of mechanical properties of polymers from molecular structure. Journal of Applied Polymer Science. 1993; 49(8): 1331-1351. doi: 10.1002/app.1993.070490802   
37. Popli R, Mandelkern L. Influence of structural and morphological factors on the mechanical properties of the polyethylene. Journal of Polymer Science, Part B, Polymer Physics. 1987; 25(3): 441-483. doi: 10.1002/polb.1987.090250301   
38. Nunes RW, Martin JR, Johnson JF. Influence of molecular weight and molecular weight distribution on mechanical properties of polymers. Polymer Engineering and Science. 1982; 22(4): 205-228. doi: 10.1002/pen.760220402   
39. Bersted BH, Anderson TG. Influence of molecular weight and molecular weight distribution on the tensile properties of amorphous polymers. Journal of Polymer Science. 1990; 39(3): 499-514. doi: 10.1002/app.1990.070390302   
40. Yun K, Park J, Jung G, Youn S. Viscoelastic constitutive modeling of solid propellant with damage. International Journal of Solids and Structures. 2016; 80: 118-127. doi: 10.1016/j.ijsolstr.2015.10.028   
41. Fatemi A, Yang L. Cumulative fatigue damage and life prediction theories: a survey of the state of the art for homogeneous materials. International Journal of Fatigue. 1998; 20(1): 9-34. doi:10.1016/S0142-1123(97)00081-9   
42. Bencher CD, Dauskardt RH, Ritchie RO. Microstructural damage and fracture processes in a composite solid rocket propellant. Journal of Spacecraft and Rockets. 1995; 32(2): 328-334. doi: 10.2514/3.26614   
43. Duncan EJS, Margetson J. A Nonlinear Viscoelastic Theory for Solid Rocket Propellants Based on a Cumulative Damage Approach. Propellants, Explosives, Pyrotechnics. 1998; 23(2): 94-104. doi: 10.1002/(SICI)1521-4087(199804)23:2&l;94::AID-PREP94>3.0.CO;2-C   
44. Dartois S, Nadot-Martin C, Halm D, Dragon A, Fanget A, Contesse, G. Micromechanical modelling of damage evolution in highly filled particulate composites – Induced effects at different scales. International Journal of Damage Mechanics. 2013; 22(7): 927-966. doi: 10.1177/1056789512468916   
45. Xu F, Aravas N, Sofronis P. Constitutive modeling of solid propellant materials with evolving microstructural damage. Journal of the Mechanics and Physics of Solids. 2008; 56(5): 2050-2073. doi: 10.1016/j.jmps.2007.10.013   
46. Mullins L. Effect of stretching on the properties of rubber. Rubber Chemistry and Technology. 1948; 21(2): 281-300. doi: 10.5254/1.3546914   
47. Dargazany R, Khiêm VN, Navrath U, Itskov M. Network evolution model of anisotropic stress softening in filled rubber-like materials: parameter identification and finite element implementation. Journal of Mechanics of Materials and Structures. 2012; 7(8-9): 861-885. doi: 10.2140/jomms.2012.7.861   
48. Diani J, Fayolle B, Gilormini P. A review on the Mullins effect. European Polymer Journal. 2009; 45(3): 601-612. doi: 10.1016/j.eurpolymj.2008.11.017   
49. Mullins L, Tobin NR. Theoretical Model for the Elastic Behavior of FillerReinforced Vulcanized Rubbers. Rubber Chemistry and Technology. 1957; 30(2): 555-571. doi: 10.5254/1.3542705   
50. Diani J, Brieu M, Vachernd JM. A damage directional constitutive model for Mullins effect with permanent set and induced anisotropy. European Journal of Mechanics - A/Solids. 2006; 25(3): 483-496. doi: 10.1016/j.euromechsol.2005.09.011   
51. Dorfmann A, Odgden RW. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. International Journal of Solids and Structures. 2004; 41(7): 1855-1878. doi: 10.1016/j.ijsolstr.2003.11.014   
52. Dorfmann A, Ogden RW. A pseudo-elastic model for loading, partial unloading and reloading of particle-reinforced rubber. International Journal of Solids and Structures. 2003; 40(11): 2699-2714. doi: 10.1016/S0020-7683(03)00089-1   
53. Minano M, Montans FJ. A new approach to modeling isotropic damage for Mullins effect in hyperelastic materials. International Journal of Solids and structures. 2015; 67-68: 272-282. doi: 10.1016/j.ijsolstr.2015.04.027   
54. Cantournet S, Desmorat R, Besson J. Mullins effect and cyclic stress softening of filled elastomers by internal sliding and friction thermodynamics model. International Journal of Solids and Structures. 2009; 46(11-12): 2255-2264. doi: 10.1016/j.ijsolstr.2008.12.025   
55. Arruda E M, Boyce MC. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. Journal of Mechanics and Physics of Solids. 1993; 41(2): 389-412. doi: 10.1016/0022-5096(93)90013-6   
56. Marckmann G, Verron E, Gornet L, Chagnon G, Charrier P, Fort P. A theory of network alteration for the Mullins effect. Journal of the Mechanics and Physics of Solids. 2002; 50(9): 2011-2028. doi: 10.1016/S0022-5096(01)00136-3   
57. Arruda EM, Boyce MC. Evolution of plastic anisotropy in amorphous polymers during finite straining. International Journal of Plasticity. 1993; 9(6): 697-720. doi: 10.1016/0749-6419(93)90034-N   
58. Diani J, Brieu M, Gilormini P. Observation and modeling of the anisotropic visco-hyperelastic behavior of a rubberlike material. International Journal of Solids and Structures. 2006; 43(10): 3044-3056. doi: 10.1016/j.ijsolstr.2005.06.045   
59. Qi HJ, Boyce MC. Constitutive model for stretch-induced softening of the stress-stretch behavior of elastomeric materials. Journal of the Mechanics and Physics of Solids. 2004; 52(10): 2187-2205. doi: 10.1016/j.jmps.2004.04.008   
60. Rebouah M, Chagnon G. Permanent set and stress-softening constitutive equation applied to rubber-like materials and soft tissues. Acta Mechanica. 2013; 225: 1685-1698. doi: 10.1007/s00707-013-1023-y   
61. Rottach DR, Curro JG, Budzien J, Grest GS, Svaneborg C, Everaers R. Permanent set of cross-linking networks: Comparison of theory with molecular dynamics simulations. Macromolecules. 2006; 39(16): 5521-5530. doi: 10.1021/ma060767x   
62. Rottach, DR, Curro JG, Grest GS, Thompson AP. Effect of Strain History on Stress and Permanent Set in Cross-Linking Networks: A Molecular Dynamics Study. Macromolecules. 2004; 37(14): 5468-5473. doi: 10.1021/ma049723j   
63. Du Y, Zheng J, Yu G. Storage life prediction under pre-strained thermallyaccelerated aging of HTPB coating using the change of crosslinking density. Defense Technology. 2020; 17(4): 1387-1394. doi: 10.1016/j.dt.2020.07.008   
64. Christiansen AG, Layton LH, Carpenter RL. HTPB Propellant Aging. Journal of Spacecraft. 1981; 18(3). doi: 10.2514/3.57807   
65. Heller RA, Singh MP. Thermal Storage Life of Solid-Propellant Motors. Journal of Spacecraft. 1983; 20(2): 144-149. doi: 10.2514/3.28371   
66. Biggs GL, Nestor III JJ. Cumulative damage model for structural analysis of filled polymeric materials. US Patent US6301970B1. 2001.   
67. Biggs GL. Forecasting Structural Reliability of Rocket Solid Propellants over Time. Advances in Rocket Performance Life and Disposal. 2002; 23-26. Published in RTO-MP-091   
68. Layton LH. Chemical Structural Aging Effects. Thiokol/Wasatch Division, Thiokol Corporation; Technical Report-Special AFRPL-TR-73-27. 1973.   
69. Layton LH. Chemical Aging Studies on ANB-3066 and TP-H1011 Propellants. Thiokol/Wasatch Division, Thiokol Corporation; Technical Report-Special. AFRPL-TR-74-16. 1974.   
70. Layton LH. Chemical Structural Aging Studies on an HTPB Propellant. Thiokol/Wasatch Division, Thiokol Corporation; Technical Report-Special. AFRPL-TR-75-13. 1975.   
71. Rott N. Note on the History of the Reynolds Number. Annual review of fluid mechanics. 1990; 22: 1-12. doi: 10.1146/annurev.fl.22.010190.000245   
72. Celina M, Minier L, Assink R. Development and application of tools to characterize oxidative degradation of AP/HTPB/Al propellant in a propellant reliability study. Thermochimica Acta. 2002; 384(1-2): 343-349. doi: 10.1016/S0040-6031(01)00793-6   
73. Johnson RA, Wichern D. Multivariate Analysis. Wiley StatsRef: Statistics Reference Online. 2015; doi: 10.1002/9781118445112.stat02623.pub2   
74. Gower JC. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika. 1966; 53(3-4): 325-338. doi: 10.1093/biomet/53.3-4.325   
75. Rencher AC. Methods of Multivariate Analysis. Second Edition. Wiley Interscience. 2002; Chapter 14.   
76. Johnson RA, Wichern DW. Applied Multivariate Statistical Analysis. Sixth Edition. 2007. Chapter 12   
77. Singh S, Rai P. A Survey of Clustering Techniques. International Journal of Computer Applications. 2010; 7(12).   
78. Everitt BS. Unresolved Problems in Cluster Analysis. Biometrics. 1979; 35: 169-181. doi: 10.2307/2529943   
79. Murtagh F. A Survey of Recent Advances in Hierarchical Clustering Algorithms. The Computer Journal. 1983; 26(4): 354-359. doi: 10.1093/comjnl/26.4.354   
80. Chen D, Chi DW, Wang CX, Wang ZR. A Rough Set-Based Hierarchical Clustering Algorithm for Categorical Data. International Journal of Information Technology. 2006; 12(3): 149-159.   
81. Gerstengarbe FW, Werner PC, Fraedrich K. Applying Non-Hierarchical Cluster Analysis Algorithms to Climate Classification: Some Problems and their Solution. Theoretical and Applied Climatology. 1999; 64: 143-150. doi: 10.1007/s007040050118   
82. Scheibler D, Schneider W. Monte Carlo Test of the Accuracy of Cluster Analysis Algorithms: A Comparison of Hierarchical and Nonhierarchical Methods. Journal of Multivariate Behavioral Research. 1985; 20(3): 283-304. doi: 10.1207/s15327906mbr2003_4   
83. Barreto S, Ferreira C, Paixão J, Santos BS. Using clustering analysis in a capacitated location routing problem. European Journal of Operational Research. 2007; 179(3): 968-977. doi: 10.1016/j.ejor.2005.06.074   
84. Henry DB, Tolan PH, Gorman-Smith D. Cluster Analysis in Family Psychology Research. Journal of Family Psychology. 2005; 19(1): 121-132. doi: 10.1037/0893-3200.19.1.121   
85. Fischer EW, Wendorff JH, Dettenmaier M, Lieser G, Voight-Martin I. Chain Conformation and Structure in amorphous Polymers as revealed by X-ray, Neutron, Light and Electron Diffraction. Journal of Macromolecular Science. 1976; 12(1): 41-59. doi: 10.1080/00222347608215172   
86. Podešva J, Dybal J, Spěváček J, Štěpánek P, Černoch P. Supramolecular Structures of Low-Molecular-Weight Polybutadienes, as Studied by Dynamic Light Scattering, NMR and Infrared Spectroscopy. Macromolecules. 2001; 34(26): 9023-9031. doi: 10.1021/ma011220f   
87. Xu M, MacKnight WJ, Chen-Tsai CGT, Thomas EL. Structure and Morphology of Segmented Polyurethanes: 4. Domain structures of different scales and the Composition Heterogeneity of the Polymers. Polymer. 1987, 28(13): 2183-2189. doi: 10.1016/0032-3861(87)90373-9   
88. Podzimek S. Light Scattering, size exclusion chromatography and asymmetric flow field flow fractionation. Chapters 3 and 5. Book, Wiley & Sons. 2010.   
89. Rastogi RP, Kishore K, Gurdip S. Solid propellant decomposition studies by differential scanning calorimetry. Thermochimica Acta. 1975; 12(1): 89-96. doi: 10.1016/0040-6031(75)85012-X   
90. de la Fuente JL. An analysis of the thermal aging behavior in highperformance energetic composites through the glass transition temperature. Polymer Degradation and Stability. 2009; 94(4): 664-669. doi: 10.1016/j.polymdegradstab.2008.12.021   
91. Goncalves RFB, Silva RP, Rocco JAFF, Iha K. Thermal Decomposition Kinetics of Aged Solid Propellant Based on Ammonium Perchlorate - AP/HTPBBinder. 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. 2008; doi: 10.2514/6.2008-4969   
92. Rocco J, Lima J, Frutuoso A, Iha K, Ionashiro M, Matos J. Thermal degradation of a composite solid propellant examined by DSC. Journal of Thermal Analysis and Calorimetry. 2004; 75(2): 551-557. doi: 10.1023/b:jtan.0000027145.14854.f0   
93. Farhadian AH, Tehrani MK, Keshavarz MH, Karimi M, Darbani SMR, Rezayi AH. A novel approach for investigation of chemical aging in composite propellants through laser-induced breakdown spectroscopy (LIBS). Journal of Thermal Analysis and Calorimetry. 2015; 124: 279-286. doi: 10.1007/s10973-015-5116-9   
94. Strobl M, Manke I, Karkjilov N, Hilger A, Dawson M, Banhart J. Advances in neutron radiography and tomography. Journal of Physics D: Applied Physics. 2009; 42(24). doi: 10.1088/0022-3727/42/24/243001   
95. Berger H. Practical applications of neutron radiography. Book, Library of Congress Catalog Card Number: 75-13061. 1976.   
96. Genix AC, Oberdisse J. Structure and dynamics of polymer nanocomposites studied by X-ray and neutron scattering techniques. Current Opinion in Colloid & Interface Science. 2015; 20(4): 293-303. doi: 10.1016/j.cocis.2015.10.002   
97. Banc A, Genix AC, Dupas C, Sztucki M, Schweins R, Appavou MS, Oberdisse J. Origin of Small-Angle Scattering from Contrast-Matched Nanopartices: A Study of Chain and Filler Structure in Polymer Nanocomposites. Macromolecules. 2015; 48(18): 6596-6605. doi: 10.1021/acs.macromol.5b01424   
98. Banc A, Genix AC, Chirat M, Dupas C, Caillol S, Sztucki M, Oberdisse J. Tuning Structure and Rheology of Silica–Latex Nanocomposites with the Molecular Weight of Matrix Chains: A Coupled SAXS–TEM–Simulation Approach. Macromolecules. 2014; 47(9): 3219-3230. doi: 10.1021/ma500465n   
99. Tung WS, Bird V, Composto RJ, Clarke N, Winey KI. Polymer Chain Conformations in CNT/PS Nanocomposites from Small Angle Neutron Scattering. Macromolecules. 2013; 46(13): 5345-5354. doi: 10.1021/ma400765v   
100. Rogante M, Lebedev VT. Microstructural characterization of polymeric materials by small angle neutron scattering. Polymer Engineering and Science. 2007; 47(8): 1213-1219. doi: 10.1002/pen.20760