Research Article
Electronic Navigation System based on the use of Alternate Coordinate System and Polar Stereographic Projection for UAVs operating in Polar Regions
Department of Industrial, Manufacturing, and Systems Engineering, Texas Tech University, Lubbock, TX, USA
*Corresponding author: Ali Kissai, Department of Industrial, Manufacturing, and Systems Engineering, Texas Tech University, Texas, USA, E-mail: Ali.kissai@ttu.edu
Received: April 12, 2019 Accepted: May 8, 2019 Published: May 16, 2019
Citation: Kissai A, Smith M. Electronic Navigation System based on the use of Alternate Coordinate System and Polar Stereographic Projection for UAVs operating in Polar Regions. Int J Aeronaut Aerosp Eng. 2019; 1(2): 46-53. doi: 10.18689/ijae-1000107
Copyright: © 2019 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
There is a large need for improving aircraft navigation safety, navigation performance in terms of time and fuel savings in the Polar Regions. Current UAV navigation systems do not fully support polar navigation. There is also a great need to making the current polar navigation methods less complex to the aircraft crew by making a large portion of the polar navigation process computerized. Current methods still present confusion or require the full attention of the crew when it comes to navigating using true north coordinate system in the Polar Regions. This paper will examine the use of a new coordinate system of piloting a drone in the Polar Regions. It will first provide an overview of the current state and limitations of the drone navigation in high latitude regions. This study is limited to the use of UAVs in the high latitude regions. To overcome the challenges of true north coordinate system over the polar region and make navigation safer and reliable, this paper focuses on the use of the equatorial coordinate system as an alternative to the use of true north based geographic coordinate system.
Keywords: Electronic Navigation System; Stereographic Projection; Alternate Coordinate System; Polar Regions.
Abbreviations: AFDS: Autopilot Flight Director System; CZM: Conventional Zero Meridian; ECEF: Earth Centered Earth Fixed; FAA: Federal Aviation Administration; FMS: Flight Management System; GPS: Global Positioning System; LNAV: Lateral Navigation; NED: North East Down; NEDE: North East Down for Equatorial Coordinates; UAV: Unmanned Aerial Vehicle; HDG: Heading.
Introduction
In recent years with so much interest in global warming scientists have started monitoring the alteration rate of the polar landscape. In the Arctic, a drastic decline in sea ice is opening new commercial routes and new opportunities for business explorations. In Antarctica, a collapse of the western ice sheet could raise global sea levels and inundate the worldʼs coasts. It is therefore crucial to monitor the state of sea ice in these regions. Satellite models and forecasts help in monitoring the state of ice decay in the Polar Regions but, these models are not sufficient as we need higher resolution coverage that can only be achieved by imagery taken from airplanes or helicopters. These missions can be expensive and extremely challenging. Furthermore, due to extreme weather in these regions, using human pilots for long range missions is risky and expensive. It is also known that the convergence of the meridians presents complications with true heading. When flying “great circle” courses at latitudes greater than 67 degrees, convergence of the meridians will cause rapid changes in true headings and true courses with small changes in aircraft position. Small distance variations can cause large variation in heading. As a result, according to the Journal of Aeronautics procedures, when using the true north coordinate system, relatively small errors in determining the aircraftʼs actual position can produce very large errors in determining the proper heading to fly and maintain the assigned flight path [1]. When even small errors occur, very large navigation errors can develop over extremely short distances. An extreme example of this phenomenon occurs at the earthʼs geographic North Pole. Despite all these issues with true heading, the currently only acceptable method of navigating through the high latitude region is using long-range navigation systems using inertial and GPS based FMS systems referenced to True North only. With commercial airlines using polar routes for time saving and fuel optimization, soon the skies over the polar regions will be crowded with manned and unmanned aerial vehicles. Current UAV navigation methods also rely only on the true north coordinate system and are not polar capable. As technology develops in this area, additional usage of polar capable drones will be the launch of UAV systems from sub marines or icebreakers to survey the surrounding terrain and provide valuable information with respect to ice monitoring [2]. This paper will provide a new coordinate system along with the polar stereographic projection as best navigation methods and practices while flying UAV in the polar regions. The findings can be used by the airline industry and the FAA to identify factors of interest in managing the polar airspace which in the future will be shared between manned and unmanned aircrafts, as well as establishing new requirements for safety in polar navigation. Since current drones are not polar capable, resolving this issue will improve navigation safety by helping to prevent fatal collision with other aircrafts in the area. It will also improve accuracy in high latitude navigation for both manned and unmanned aircrafts operating in the polar regions.
The Challenges of Geographic Coordinate system based Navigation in the Polar Regions
Navigating a UAV in high latitudes using true heading on great circle poses a big challenge in the sense that the heading will change constantly along the great circle route. This is because meridian lines crowd together as you get close to the North Pole causing true heading to become almost useless due to constant changes over small distances. As we get close to the North Pole true heading becomes obsolete. This makes the geographic coordinate system unusable in these regions. The following statement from the Boeing Aero Magazine Journal [3] accurately describes the problem: “When a North Pole (N90EXXXXX or N90WXXXXX) or South Pole (S90EXXXXX or S90WXXXXX) waypoint is used near the poles, a rapid heading and track reversal occurs as the airplane passes over the waypoint. If the airplane is operating in HDG SEL or HOLD mode while near either pole, the crew will need to rapidly update the heading selector to reflect the changing or reversed heading. Otherwise, the autopilot flight director system (AFDS) will command an unwanted turn. For autopilot operation in the polar region using a roll mode other than LNAV, the TRUE position on the heading reference switch should be selected. However, LNAV is the preferred roll mode [3]. Also, there are issues with GPS updates after crossing 88.5 degrees latitude while flying toward the pole, and the crew must gradually phase out position and velocity corrections before the pole is crossed. These problems can be avoided by using an alternate coordinate system; for simplicity this new coordinate system could be a pole origin located somewhere in the equator and therefore rendering all heading and direction at the high latitudes well defined and removing all mathematical singularities.
Geographic coordinate Navigation System and the ECEF
The ECEF earth centered earth fixed coordinate system rotates with the earth around its spin axis. Consequently, any fixed point on the earth surface has a unique set of coordinates.
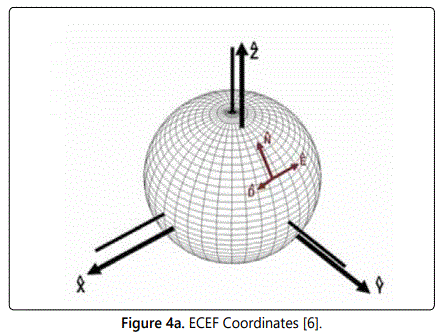
The origin and axes of the ECEF coordinate system are shown in figure 1 and are defined as follows:
Coordinate Systems and Transformations
1. The origin is denoted by Oe and is located at the center of the earth.
2. The Z-axis is denoted by Ze and is along the spin axis of the earth, pointing to the North Pole.
3. The X-axis is denoted by Xe and intersects the sphere of the earth at 0° latitude and 0° longitude.
4. The Y-axis is denoted by Ye and is perpendicular to the Z- and X-axes with the usual right-hand rule.
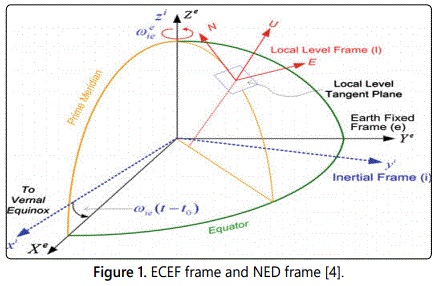
The subscript e is used to denote Coordinate vectors expressed in the ECEF frame.
The position vector in the ECEF coordinate system frame is denoted by Pe=(xe, ye, ze).
The geodetic coordinate system (see figure 2a) is widely used in GPS-based navigation.
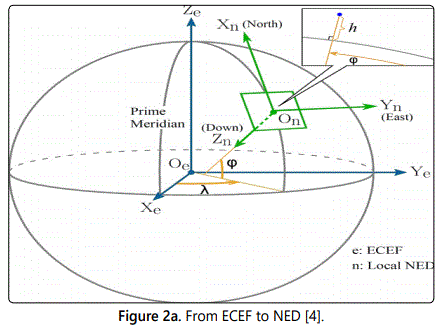
This system characterizes a coordinate point near the earthʼs surface in terms of longitude denoted by λ, latitude denoted by ϕ, and height also known as altitude denoted by h. The longitude measures the angle between the Prime Meridian and the measured location ranging from−180° to 180°. The latitude ranges from −90° to 90° and measures the angular distance north or south from the equator to the point of interest on the earthʼs surface. The height also referred to as altitude is the local vertical distance between the measured point and the referenced spherical or ellipsoid model of earth. We denote Coordinate vectors expressed in terms of the geodetic frame as P (λ ϕ h). The key parameters associated with the geodetic frame include
1. The semi-major axis REa,
2. The flattening factor f,
3. The semi-minor axis REb,
4. The first eccentricity e,
5. The meridian radius of curvature ME, and
6. The prime vertical radius of curvature NE [4].
Transforming the position vector from the geodetic system to the ECEF coordinate system is a necessary step in converting the GPS position measurement to the local NED (North East Down) coordinate system.
The NED coordinate system also known as a navigation coordinate system is a coordinate frame fixed to the earthʼs surface. Based on the WGS 84 ellipsoid model, its origin and axes are defined as the following: [4]
1. The origin (denoted by On) is arbitrarily fixed to a point on the earthʼs surface.
2. The X-axis (denoted by Xn) points toward the ellipsoid north (geodetic north).
3. The Y-axis (denoted by Yn) points toward the ellipsoid east (geodetic east).
4. The Z-axis (denoted by Zn) points downward along the ellipsoid normal. The local NED frame plays a major important role in navigation in the sense that Navigation of small-scale UAV is developed using this NED frame. The subscript n is used to denote Coordinate vectors expressed in the local NED coordinate system. More specifically, the position vector is Pn, the velocity vector is Vn, and the acceleration vector is an in the NED coordinate system and are defined as Pn=(xn, yn, zn), Vn=(un, vn, wn), An=(ax,n, ay,n, az,n)
Transformation from Geodetic to ECEF Coordinates
Given a geographic geodetic point, say Pg=(λ, ϕ, h), where λ is latitude, ϕ is longitude, and h is altitude its planar coordinates in the ECEF frame is given by
Pe=(xe, ye, ze) defined as Pe=((Ne+h) Cos(ɸ)Cos(λ), (Ne+h) Cos(ɸ)Sin(λ), Ne(1-e2)+h) Sin(ɸ))
Where e and Ne are defined as follows [4]:
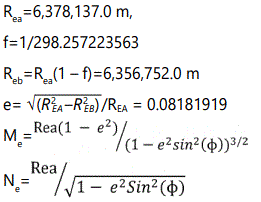
Position errors in polar regions while in Geographic coordinates system
Because of the rapid convergence of earth meridians in high-latitude areas, small position errors will cause large divergence in longitude. So, a better way to express the UAV position would be in the following form in earth e coordinates system (Figure 2b). It is expressed in this form:
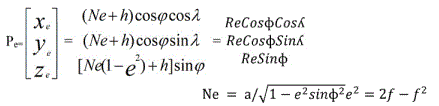
Here ɸ is latitude and ʎ the longitude; the position error can be estimated by the below equations [5]

Position Errors in terms expressed in Geographic Coordinates.
This error model will be used in both coordinate systems to compare position error.
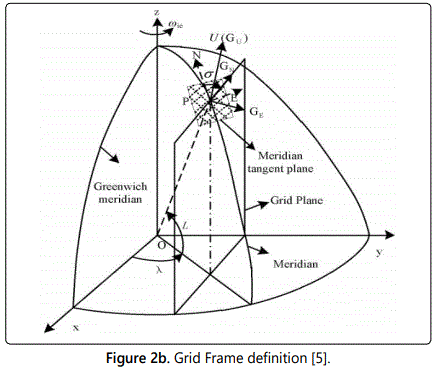
The position error is defined as the latitude error and the longitude error. The latitude of a point on the earth is defined as the angle subtended by the direction of the vertical at that point and the equatorial plane [5]. The geodetic meridian is defined as the plane through the normal and the minor axis of the reference ellipsoid and so, the geodetic longitude of a point is the angle between its meridional plane and the CZM (Conventional Zero Meridian) [6]. The latitude and longitude errors are defined above. This section describes the process for determining position and attitude errors specifically position errors expressed in terms of earth frame and position and attitude errors expressed in terms of Geographic coordinates.
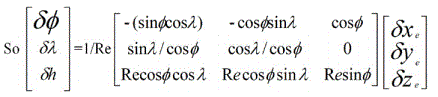
The independent variables are position, course, heading and the dependent variables are the corresponding errors.
This analysis will look into theoretical heading errors both in lower latitudes and higher latitudes.
Let the e Frame be the earth centered earth fixed frame, g frame be the geographic frame and G frame be the grid frame; going from grid north to the geographic north is done thru a rotation of б described by CGg below; going from geographic north to earth fixed frame e gives the matrix Cge below
Going from earth fixed frame to grid frame involves the product of 2 matrices Cge CCGg= CGe [5]
The figure 6 below shows the descriptions of these rotations.
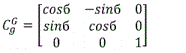
Transformation matrix from Grid North to Geographic North.
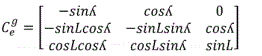
Transformation matrix from geographic North to Earth fixed.
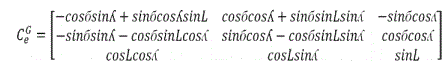
Transformation matrix from Grid North to Earth fixed.
The attitude error can be estimated by the following equations [5] setting W=Wie
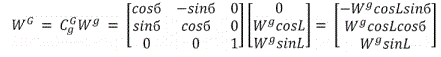
Attitude equation in Grid Frame
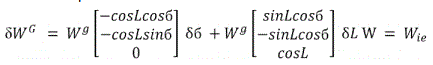
Attitude equation in Grid Frame
Heading Error
By definition Heading is the angle between the direction in which the objectʼs nose is pointing and a reference direction (ex. true north). An aircraftʼs heading is the direction that the aircraftʼs nose is pointing. It is referenced by using either the magnetic compass or heading indicator, two instruments that most aircraft have as standard. Using standard instrumentation, it is referenced to the local magnetic north direction. True heading is in relation to the lines of meridian and is the objectʼs direction with respect to Geographic North. The following equations describe the attitude errors in the grid frame with respect to the geographic frame.
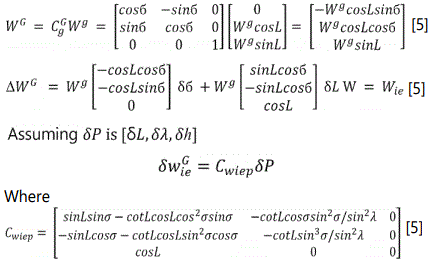
Recall that G is the Grid frame and g is the geographic frame True North, see figure 3 below
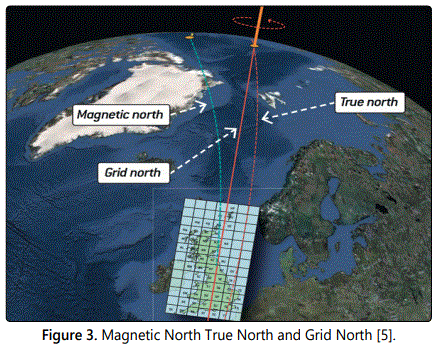
Appendices 1 and 2 show data generated in lower latitudes and higher latitudes by fixing the latitude values and varying the longitude from 0 to 360; in these appendices theoretical equations are used to compute lower latitude heading errors under the following assumptions: the computation assumes WGS84 model, assume we are given the Cartesian coordinates errors dx and dy varied between 0 and 35 m uniformly. The vector heading error δ W components are calculated. The variance, the mean and standard deviations are calculated for both latitude errors and longitude errors. σ is the angle going from geographic to grid frame. The attitude error expressed in function of the position variation is:
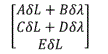
Where A= -sinLsinσ-cotLcosLcos2σsinσ
B= -cotLcosσsin2σ/sin2λ
C= -sinLcosσ-cotLcosLsin2σcosσ
D= -cotLsin3σ/sin2λ
E=cos(L) and σ =arcSin (sinλsinL/sqrt(1-(cosLsin2λ) [5]
Consider the following hypothesis:
H0: High latitude Heading errors are identical to low latitude Heading errors.
H1: High latitude Heading errors are far greater than low latitude Heading errors.
Given a vector heading errors x, y components at higher latitude shown in Appendix 2 (High latitudes Heading errors) its z score is defined by z=sqrt (N)* (x-u)/σ where u and σ are the mean and standard deviations of heading errors components in lower latitudes (Appendix 1). From the high latitude heading errors components computations in the attached spreadsheet (Appendix 2), it shows that the average heading x, y components errors are-3.776E+17, 8.4188E+16 see Appendix 2 high latitude heading errors. The corresponding z score are respectively 1.19178E+15, 1,348E+13 in Appendix 2 which leads to a probability value of 0. From our previous assumptions we assume a level of confidence C of 0.95; hence α=0.05. The critical Z score values when using a 95% confidence level are -1.96 and +1.96 standard deviations. The p-value associated with a 95% confidence level is 0.05. When the Z score is between -1.96 and +1.96, then the p-value will be greater than 0.05, and the null hypothesis cannot be rejected. Our P value will be the Probability of obtaining in the northern latitudes a sample with mean error less or equal the mean error observed in the lower latitudes assuming H0 is true; but since our P value is 0 less than α=0.05 we therefore reject the null hypothesis on the heading. We conclude that High latitude Heading errors are far greater than low latitude Heading errors. For this reason, we need to consider the use of the equatorial coordinate system. Appendix 2 for high latitude heading errors x,y as we get close to the north pole shows Z scores that are 1.08781E+17 and 9.86838E+16 magnitude larger than the mean heading error in low latitude while using the geographic coordinate system. The equations derived in the Alternate Coordinate Navigation System section and the Equatorial Coordinates System section show that the decrease in the magnitude of the navigation errors that result in using the equatorial coordinate system in the polar regions will be identical to the navigation errors observed in low latitude navigation while using geographic coordinate system as show in Appendix 1. This is also due to the fact by shifting the origin from the pole to the equator, headings with respect to the new pole become now well defined and the new meridians for the equatorial coordinate system will no longer converge at the north pole but rather be rectangular.
Alternate Coordinate Navigation System
Given a geodetic point, say Pg=(λ ϕ h), its planar coordinates in the ECEF frame is given by Pe=(Xe Ye Ze) then to obtain the geodetic point Pa (λa ϕa ha) in the alternate coordinate system the equations will be derived based on the location of the origin of the alternate coordinate system.
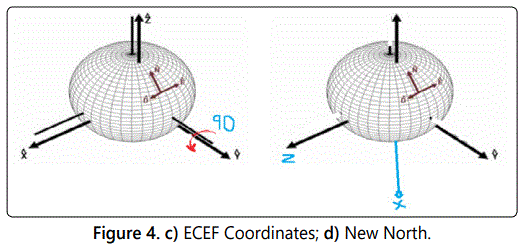
We need to redefine the reference location when the UAV is flying in the high latitude regions. The north is defined with respect to the positive Z axis in the ECEF frame; a new north can be obtained by rotating the z axis clockwise (90 degrees) or counter clockwise (90 degrees) about the ECEF y axis as shown in the figures 4a and 4b.
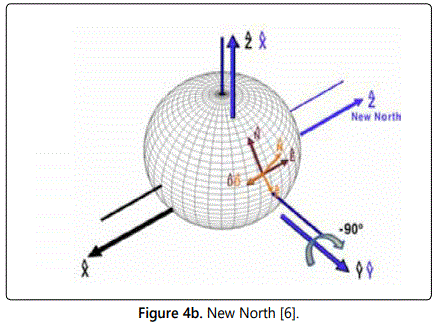
We define the position in the new alternate coordinate system as (XA, YA, ZA); we can obtain a transformation from (XA, YA, ZA) to (X, Y, Z) because we know the rotation sequence. In the new transformation XA became Z, YA became Y no change; and ZA became –X; therefore, this translates in the following mathematical transformation

The new alternative Latitude and alternative Longitude position of the UAV is known as transverse coordinates. Now we can compute any UAV position in this transverse coordinate system; the same geodetic equations relating (X, Y, Z) to (λ, φ, h) can be applied. Given a geographic geodetic point, say Pg=(λ ϕ h), its coordinates in the ECEF frame is given by Pe=(Xe, Ye, Ze) defined as
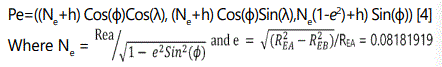
We can set Pe=(RCos(ɸ)Cos(λ), RCos(ɸ)Sin(λ), RSin(ɸ)) where R=Ne+h
Therefore 1) X=RCos(ɸ)Cos(λ), Y=RCos(ɸ)Sin(λ) Z=R2Sin(ɸ) [4]
Likewise, the position in the Transverse coordinate system is given as
2) XA=RCos(ɸA)Cos(λA) YA=RCos(ɸA)Sin(λA), ZA=R2 Sin(ɸA) from the above transformation we have that XA=Z, YA=Y, ZA=-X hence RCos(ɸA)Cos(λA)=R2 Sin(ɸ)R2 Sin(ɸA)=-RCos(ɸ)Cos(λ)=>ɸA=RarcSin(-Cos(ɸ)Cos(λ)).1/R2 [4]
We can also say that ZA/XA=Z/X this means that λA=R arc Tan (sin(λ)/tan(ɸ)).1/R2
So Pg=(λ ϕ h) in the geographic coordinates system becomes PA=(λA, ϕA, h) in the transverse coordinate system with λA=R arc Tan (sin(λ)/tan(ɸ)).1/R2
and ɸA=R.arc Sin(Cos(ɸ)Cos(λ)).1/R2 [4]
Equatorial Coordinates System
Similarly, if we rotate counter clockwise we will obtain a new origin at (0, 0) and we can apply the same transformation and obtain similar transformation equations.
In the new transformation XA becomes -Z, YA becomes Y (no change); and ZA becomes X as shown in figures 4c and 4d.
Therefore, this translates in the following mathematical transformation

The physical origin of the coordinate system will be set at (lat,lon) (0,0) or (0,180) or (0,lon) where lon can be any longitude; see figure 4e below.
The new alternative Latitude and alternative Longitude position of the UAV can now be computed in the new alternative coordinate system; this new coordinate system can be named equatorial coordinates systems. The same geodetic equations relating (X, Y, Z) to (λ, φ, h) can be applied, given a geodetic point, say Pg=(λ ϕ h), its geographic coordinate in the ECEF frame is given by Pe=(xe, ye, ze) defined as Pe=((Ne+h)Cos(ɸ)Cos(λ), (Ne+h)Cos(ɸ)Sin(λ),Ne(1-e2)+h)Sin(ɸ))
We can set Pe=(RCos(ɸ)Cos(λ), RCos(ɸ)Sin(λ), RSin(ɸ)) where R=Ne+h
Therefore 1) X=RCos(ɸ)Cos(λ), Y=RCos(ɸ)Sin(λ)Z=R2Sin(ɸ)
Likewise, the position in the Equatorial coordinate system is given as Pe=(λe, ϕe, he)
2) Xe=RCos(ɸe)Cos(λe), Ye=RCos(ɸe)Sin(λe), Ze=R2 Sin(ɸe)
From the above transformation we have that XA=-Z, YA=Y, ZA=X hence R2 Sin(ɸe)=RCos(ɸ)Cos(λ)=>ɸe=RarcSin(Cos(ɸ)Cos(λ)).1/R2λe can be obtained using a similar technique as above and we get that
λe= -R arcTan (sin(λ)/tan(ɸ)).1/R2
The following transformation allows moving a vector from True North based Ground coordinate system NED to equatorial based Ground Coordinate System NEDT; here Lʼ, ʎʼ, are the equatorial latitudes and longitudes and L, ʎ, are the geographic latitudes and longitudes [6].
First from ECEF to NED see figure 1. 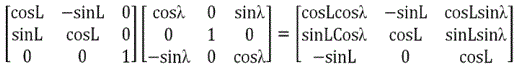
Second from ECEF to NED Equatorial we have
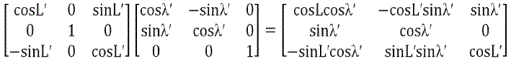
Therefore, a vector V[Vn, Ve,Vd] from NED to NEDʼ equatorial V[Vʼn,Vʼe,Vʼd] can be expressed as:
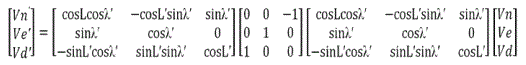
Projections and Transformations
In the polar regions we will use polar stereographic projection to convert from latitude, longitude to planar coordinates x, y. According to the NASA distributed Active Archive Center [5] Polar stereographic projection specifies a projection plane or grid tangent to the Earthʼs surface at 70 degrees northern and southern latitude. This planar grid is designed so that the grid cells at 70 degrees latitude are exactly the nominal grid resolution. From the National Snow and Ice Data Center, distortion in the grid increases as the latitude decreases because any given grid cell will contain larger earth surface; this can be quite significant in the northern grid where distortion go up to 31 percent. For the southern grid, the grid maximum distortion is up to 22 percent [5].
The polar stereographic formula allowing conversion between latitude/longitude and x-y grid coordinates are obtained from map projections used by the U.S. Geological Survey [7].
From Equatorial coordinates to screen coordinates system for the Spherical Model
The following algorithm provides a transformation from Equatorial coordinates (ʎ, ɸ) to screen coordinates (x, y) using Polar Stereographic projection assuming spherical model [7]. The Polar Stereographic projection is a particular function that projects the sphere onto a plane.
The transformation equations for a sphere of radius R are given by
X = kcos(ɸ) sin (ʎ - ʎ0)
where ʎ0 is the central longitude, ɸ1 is the central latitude, and 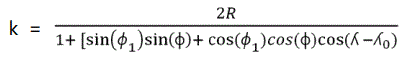 [7] then the screen coordinates (x,y) are defined as (x,y)=Scale Factor*(X,Y).
[7] then the screen coordinates (x,y) are defined as (x,y)=Scale Factor*(X,Y).
From Screen coordinates to Equatorial coordinates system for the Spherical Model
Given the planar coordinates (X,Y) which are defined as (X,Y)= Scale Factor*(x,y) where (x,y) are the screen coordinates. The inverse formulas for latitude ɸ and longitude ʎ are then given by [7]
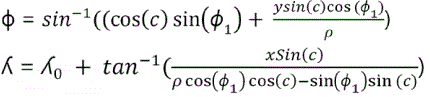
Where 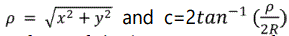 [5] and the two-argument form of the inverse tangent function is best used for this computation.
[5] and the two-argument form of the inverse tangent function is best used for this computation.
For an oblate spheroid, R can be interpreted as the “local radius,” defined by
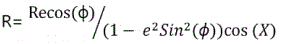
where Re is the equatorial radius and X is the conformal latitude.
From Equatorial coordinates to screen coordinates system for the Ellipsoid Model
For the ellipsoid model case If the equatorial coordinates (λ, ϕ, h) (latitude, longitude, altitude) are known, then the Cartesian coordinates are given by X=(Rn+h) cos (ϕ)cos (λ) Y=(Rn + h) cos (ϕ) sin (λ) Z=( Rn+h)sin(ϕ) 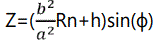 with Rn=
with Rn=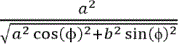 [7].
[7].
The X-coordinate is positive toward the intersection of the prime meridian and equator. The reference ellipsoid satisfies the equation 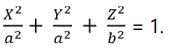
Earth Semi-major axis=a=6378.4 km, Earth Semi-minor axis=b=6356.9 km.
Here a and b, respectively, denote the semi-major and semi-minor axes of the ellipsoid. This surface can be generated by rotating an ellipse defined by 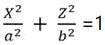 about the Z-axis. During the transformation from Equatorial coordinates to Cartesian coordinates to screen Cartesian coordinates one needs to use the forward projection equations; in this case we are given the equatorial latitude and longitude (λ, ϕ) values and we are seeking the projection plane coordinates (X,Y); (Xe, Ye);2) Xe = RCos(ɸe)Cos(λe), Ye = RCos(ɸe)Sin(λe), Ze=R2 Sin(ɸe). Next using scaling and properly setting the projection center and orientation, we can transform and properly map from the planar coordinates (X,Y) to a point F (x,y)screen coordinates.
about the Z-axis. During the transformation from Equatorial coordinates to Cartesian coordinates to screen Cartesian coordinates one needs to use the forward projection equations; in this case we are given the equatorial latitude and longitude (λ, ϕ) values and we are seeking the projection plane coordinates (X,Y); (Xe, Ye);2) Xe = RCos(ɸe)Cos(λe), Ye = RCos(ɸe)Sin(λe), Ze=R2 Sin(ɸe). Next using scaling and properly setting the projection center and orientation, we can transform and properly map from the planar coordinates (X,Y) to a point F (x,y)screen coordinates.
From Screen coordinates to Equatorial coordinates system for the Ellipsoid Model
Likewise, during the inverse transformation from screen Cartesian coordinates to planar coordinates to equatorial coordinates one needs to use the inverse projection equations; in this case we are given the screen point (x,y) values and we are seeking latitude and longitude (λ, ϕ) values. The relationship between the screen coordinates (x,y) and the planar coordinates (X,Y) is defined as (X,Y)=Scale*(x,y); as the scale varies, this provides several zoom factors on the screen. Now that we are given the screen point (X, Y) values, to obtain the equatorial latitude and longitude (λe, ϕe) values we approximate using.
The inverse formulas for latitude ɸe and longitude ʎe are then given by
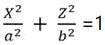
This paper showed that with the use of the equatorial coordinate system we can express a vector position, velocity, heading from ECEF to NED and from ECEF to NED equatorial. The problem of True north bearing and the challenges of using geographic coordinates near the pole can now be solved by expressing any vector V [Vn, Ve,Vd] from NED to NEDʼ equatorial V [Vʼn,Vʼe,Vʼd] as shown in the equatorial coordinates system section. This transformation makes bearing defined in the polar region with respect to the new equatorial coordinate system which is now in Africa (see figure 4E). This new coordinate system along with the use of polar stereographic projection provide more accuracy and make it easy to take a geodetic point on the polar region and transform it to a screen point on a computer screen in order to provide Electronic Navigation for UAVs flying over the polar region. With this new coordinate system meridians no longer converge at the traditional poles but rather at this equatorial coordinate system. Now when every vector such as position, heading, course, speed is expressed in the new equatorial coordinate system the following statement from Boeing Aero magazine journal [3] will no longer be an issue: “When a North Pole (N90EXXXXX or N90WXXXXX) or South Pole (S90EXXXXX or S90WXXXXX) waypoint is used near the poles, a rapid heading and track reversal occurs as the airplane passes over the way point. If the airplane is operating in HDG SEL or HOLD mode while near either pole, the crew will need to rapidly update the heading selector to reflect the changing or reversed heading. Otherwise, the autopilot flight director system (AFDS) will command an unwanted turn.”
Simulation results have shown that the latitude of switch from geographic coordinates system to the equatorial coordinates system is close to 85 degrees North or south. This is the latitude beyond which tremendous errors in navigation occur with the use of the geographic coordinate system and require constant human intervention to update heading and course [8] as stated above.
Conclusion
This paper was set to explore the use of alternative coordinate system for UAV navigation in the Polar Regions. Current drones are not polar capable and using the new equatorial coordinate systems along with the polar stereographic projection for electronic navigation will improve navigation safety by helping to prevent collision with other aircrafts in the area due to large errors in position, heading and course. It will also improve accuracy in high latitude navigation for both manned and unmanned aircrafts operating in the polar regions. Data and analysis provided showed that true heading errors are considerable in northern latitude to the point of affecting accuracy in high latitude navigation. To eliminate these errors the equatorial coordinate system was selected as a choice of an alternative coordinate system and the transformations equations were developed allowing the expression of any geographic geodetic position, heading, and course in the polar region in terms of the equatorial coordinate system. Additional transformations allowing moving a vector from True North based Ground coordinate system NED to equatorial based Ground Coordinate System NEDE are developed. These transformations facilitate the development of electronic navigation software allowing remote guidance of a UAV to operate safely and accurately in the North Pole from a remote location. The findings can also be used by the airline industry in evaluating the benefits of switching to an alternate coordinate system in the future while flying the polar regions.
References
- Aircraft Equipment and Operational Authorizations. Volume 4. 2018.
- Williams GD, Fraser AD, Lucieer A, et al. Drones in a cold climate. Eos. 2016. doi: 10.1029/2016EO043673
- Boeing Commercial Airplanes. Communication and Navigation. Aero magazine. 2017.
- Office of Geomatics. The Universal Grids and the Transverse Mercator and Polar Stereographic Map Projections. NGA.SIG.0012_2.0.0_UTMUPS. 2014.
- Yan Z, Wang L, Zhang W, Zhou J, Wang M. Polar Grid Navigation Algorithm for Unmanned Under water Vehicles. Sensors (Basel). 2017; 17(7): 1599. doi: 10.3390/s17071599
- National Snow and Ice Data Center. Polar Stereographic Projection and Grid. NASA Distributed Active Archive Center. 2018.
- Zhao L, Qiu H, Feng Y. Analysis of a robust Kalman filter in loosely coupled GPS/INS navigation system. Measurement. 2016; 80: 138-147. doi: 10.1016/j.measurement.2015.11.008


