Abstract

Cohesive zone modelling is commonly used in treating complicated damage, failure and fracture phenomena in different materials and mechanical components; however, a number of the disadvantages, difficulties or even inherent problems exist. This paper reviews some recent critical progress in cohesive zone models (CZMs) at different scales. Four new potential-based and non-potential-based CZMs proposed by McGarry et al. cleared the inherent problems with the well-known Xu-Needleman CZM. A multiscale CZM by Zeng and Li introduced a local quasi-continuum medium that obeys the Cauchy–Born rule to model the bulk material and then a coarse grained depletion potential to formulate the cohesive force and displacement relations inside the cohesive zone, based on an idea in colloidal physics. First-principle calculation of mixed-mode responses of a metal-ceramic interface by Guo et al. showed a promising way to construct an accurate interface cohesive law. A nonlocal cohesive zone model for finite thickness interfaces developed by Paggi and Wriggers are able to accounts for the complex failure phenomena affecting the material microstructure of the interface region, through a continuum damage mechanics concept. These studies provide novel constitutive laws of CZMs and open up new possibilities in improving the cohesive modeling of fracture and failure.

Keywords: Cohesive Zone; Modeling; Fracture; Mechanical Components.

Introduction

Classical fracture mechanics treats a pre-existing crack-like defect as a mathematically sharp crack. This type of continuum mechanics framework enjoyed countless successes, but also possesses several critical issues such as crack nucleation. The theory of cohesive zone model (CZM), another phenomenological continuum framework, is an alternative way to treat many of complicated damage, failure and fracture phenomena such as interfacial delamination/debonding, crack/void nucleation, and that in materials of composites, coatings/thin films, concrete, rock [1-7]. Up to now, cohesive zone approaches have vitality in that they are able to describe a wide range of issues and make good predictions or reasonable understandings, and hence have gained much popularity in basic research and engineering applications related with material failure behaviors. There is now an abundant literature on cohesive modelling, simulation of fracture. However, despite this, a number of the disadvantages, difficulties or even inherent problems have been gradually observed by researchers. Recent years witness some critical progresses in improving the common CZMs or in solving the above issues.

No attempt is made in this paper to provide a thorough overview of these efforts. Rather, some of the highlighted works are picked up to discuss a bit more clearly where the problems are and what the possible ways to tackle them are. Specifically, recent developments from four research groups are discussed in particular, including, (1) McGarry et al. and Máirtín et al. [8,9], proposal for four new potential-based and non-potential-based CZMs under mixed-mode separation and over-closure, after a comprehensive analysis of the well established CZMs; (2) Zeng and Li [10], a novel multiscale CZM being capable of simulating strong discontinuities across a solid at nanoscale, such as micro-cracks and dislocations at smallscales; (3) Guo et al. [3], an interface cohesive potential that is linked to the first-principle mixed-mode responses; (4) Paggi and Wriggers [11,12], a nonlocal cohesive zone model for finite thickness interfaces that accounts for the complex failure phenomena, through a continuum damage mechanics concept.

New Potential and Non-Potential-based CZMs for Mixed-Mode Fracture

McGarry et al. [8,9] made a thorough analysis of potentialbased and non-potential-based CZMs under conditions of mixed-mode separation and mixed-mode over-closure. Several problems are identified with the widely implemented potential-based Xu-Needleman (XN) model [6], and four new CZMs are proposed to overcome them.

Modified potential (MP) formulation
For the XN model, the critical problem is the occurrence of the non-physical repulsive normal tractions and the instantaneous negative incremental energy dissipation under displacement controlled monotonic mixed-mode separation when the work of tangential separation exceeds the work of normal separation. To solve this, McGarry et al. modified the original exponential form of the XN interface potential function ϕ, referred as MP model, as

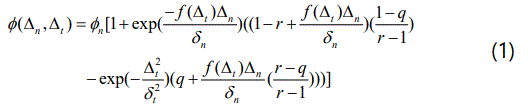
Δ_n, Δ_t are the normal and tangential components of the interface separation vector, respectively. ϕ_n , ϕ_t are the work of normal and tangential separation, respectively. δ_n, δ_t are the normal and tangential interface characteristic lengths, respectively. The parameters q and r are defined as q = ϕ_t/ϕ_n, r = Δ_n^*/ δ_n , and Δ_n^* is the value of Δ_n after complete tangential separation takes place under the condition of normal tension being zero(T_n=0). m is the interface parameter describing additional coupling between normal and tangential tractions.

The derived interface traction T–separation Δ relations are given by

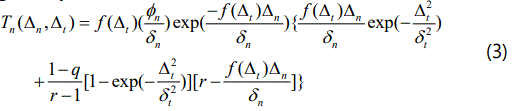
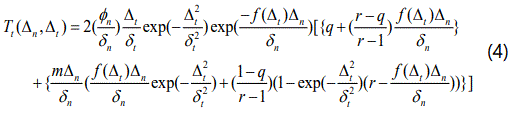
The new interface parameter, m, actually controls the zone of influence of tangential behavior for mixed-mode conditions. If m=0, the MP potential function collapses to the XN model. With the increase of parameter m, both the magnitude and the dominant region of repulsive normal tractions occur are reduced. Here an important point to note, the possibility of computing repulsive normal tractions cannot be fully eliminated for any potential-based model where the work of tangential separation exceeds the work of normal separation.

By checking the energy dissipation during monotonic loading to failure for a range of separation mode angles, it is found that the MP mode reduces the zone of repulsive normal traction and consequent negative dissipation, but at the price of increasing the magnitude of repulsive tractions within this zone. From an examination of the penalization of mixed-mode over-closure of MP model, it is seen that the penalization of tangential separation increases with increasing normal over-closure, resulting in a physically realistic penalization of mixed-mode over-closure. And an increase in the coupling parameter m, results in an increased penalization of mixedmode over-closure.

Non-potential-based CZMs
Since the XN model provides physically realistic coupling under mixed-mode separation only if q=1(q is the ratio of work of tangential separation to the work of normal separation), vanden Bosch et al. [13] proposed a coupled non-potential based CZM(the BSG model) that provides physically realistic coupling during mixed-mode separation. However, similar to the XN model, the BSG model does not provide correct penalization of mixed-mode over-closure as well, with peak tangential tractions decreasing with increasing over-closure, becoming repulsive when the normal over-closure exceeds the characteristic distance.

Non-potential-based formulation 1(NP1): To correct this unphysical behavior of the BSGCZM in mixed-mode over-closure, Mc Garry et al. further modified the form of the tangential traction–separation relationship by removing the term (1+Δ_n /δ_n). Thus, the reductions in peak tangential traction during mixed-mode over-closure is eliminated, and the resultant traction–separation relationships are

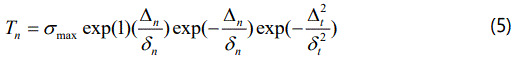
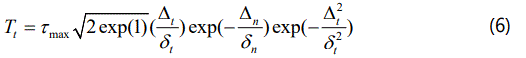
where σ_max and τ_max are the peak tractions computed during pure normal and tangential separation, respectively.

Non-potential-based formulation 2(NP2): The XN, BSG and NP1 CZMs have different forms for normal and tangential separation, and no model parameters can be chosen so that identical normal and tangential traction–separation relationships are obtained for these three models. To treat this limitation, Mc Garry et al. proposed a second non-potential-based formulation (NP2) as

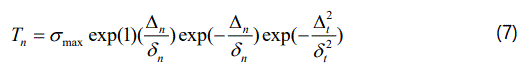
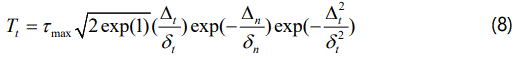
When σ_max=τ_max and δ_n=δ_t, this model provides identical behavior in normal and tangential separation. The parameters α and β represents the weighting of the mixed-mode coupling terms. The NP2 model provides identical “effective traction” – “effective separation” relationships for 90° (normal), 0° (tangential) and 45° (mixed-mode) separation in addition to providing physically realistic behavior in mixed-mode over-closure.

Separation magnitude coupling (SMC) formulation: A third non-potential-based model is constructed (so-called Separation Magnitude Coupling (SMC) formulation) in which the effective separation is used for mixed-mode coupling, as

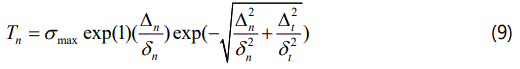
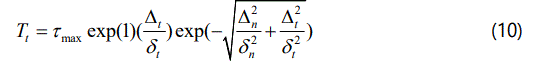
This model provides identical behavior in normal and tangential separation when σ_max=τ_max and δ_n=δ_t as well. Additionally, the traction separation equations can be derived from a potential function

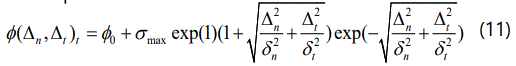
only when σ_max=τ_max and δ_n=δ_t.

The SMC model provides identical and path-independent separation if σ_max=τ_max and δ_n=δ_t, but no penalization to the mixed-mode over-closure. Thus, the SMC mode should be used in separation (Δ_n>0) only.

The above three non-potential-based cohesive zone formulations succeed in achieving a physically realistic coupling between normal and tangential tractions in mixed-mode separation and over-closure. But, further challenges appears, such as, some results from the MP model are not in agreement with experimental observation and theoretical results, and the NP1, BSG, and SMC models under traction controlled mode mixity still display certain bias or problems. That is, a mere modification to a cohesive zone model might be insufficient.

A Multiscale CZM for Interface Fracture

At present, most of CZM applications are macro scale material failure analysis and restricted to the small scale yielding conditions. When the crack size becomes very small, say below sub-micron scale, the conventional cohesive zone model may reach to its limit, since irreversible plasticity theory is highly size-dependent, and the conventional cohesive law inside the cohesive zone may become inaccurate. By taking a completely different approach, Zeng and Li [10] recently developed a novel multi scale CZM, where the cohesive zone as a finite width zone is considered and the constitutive relations in the inter planar cohesive zone is modeled by making use of the coarse graining methodology in colloidal physics.

To reduce the computational cost and complexity in computing the atomistic potential energy, the proposed multi scale CZM models the bulk material as a local quasi-continuum medium that obeys the Cauchy–Born rule. This is necessary to construct an atomistically based macro scale constitutive relation in multi scale computations.

To represent possible non-uniform local deformation fields caused by the presence of defects, such as interfaces, the interface is remodeled as a finite width compliance cohesive zone. The cohesive zone between two bulk media is remodeled as a different lattice strip region whose lattice constants and atomistic potential are different from those of the bulk medium. The main assumption adopted but the authors are that the non-uniform deformation field is mainly confined inside the cohesive zone between the adjacent bulk elements, and its effective displacement field can be treated as an affine displacement field. In other words, the effective affine displacement field inside the cohesive zone is a coarse grain model for local non-uniform displacement field. That is, in the proposed multi scale cohesive zone model, there are two coarse graining models: one for the bulk medium and one for the interfaces. The advantage of such coarse graining treatment is that the effective deformation field can be uniquely determined by the bulk finite element nodal displacements, and the coarse grain model for the cohesive zone is properly connected with the kinematics of bulk elements that are treated as a quasi-continuum.

The authors had a belief that the nature of the cohesive force inside a realistic weak interface, for instance, grain boundary, is same as the colloidal adhesive force, and its cohesive law therefore can be obtained by various coarse graining methods and the basic idea of the depletion potential in colloidal physics. Their hypothesis is that most defects are multi-scale entities, so should be the cohesive zone. Taking crack as an example, once a crack starts to grow, it will evolve into a growth of a depleted material zone, which contains voids, grain boundary, slip lines, and surface separation.

Specifically, Derjaguinʼs approximation [14] was used to find the cohesive potential inside the cohesive zone. Because the cohesive zone is considered as a physical zone with dimension, the local version of quasi-continuum method is applied to obtain a coarse grained stress–strain relation. For instance, the first Piola–Kirchhoff stress inside the cohesive zone can be written as:

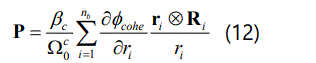
where β_c is the adjustable factor for equivalent cohesive zone lattice density, Ω^c₀ is the volume of the a unit cell inside the cohesive zone, and ϕ_cohe is the so-called depletion potential inside the cohesive zone. r_i is an arbitrary deformed bond vector in a unit cell and is the un deformed bond vector.

To obtain the depletion potential, the key in this model, the cohesive zone is assumed as a compliance interface and much weaker than the adjacent bulk elements. Thus, when calculating the interaction between two material points inside the cohesive zone and the bulk medium, the bulk medium is considered as a rigid with almost no deformation, so the two bulk elements adjacent to the compliant cohesive zone may be viewed as two rigid body half spaces. Therefore, if the atomistic potential for a given bulk medium is available, say a pair potential, the atomistic potential of the cohesive zone can be obtained by integrating the bulk potential over the rigid bulk medium half space.

For example, when using Lennard-Jones potential as the bulk potential

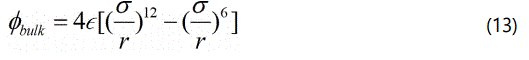
the interface depletion potential will be

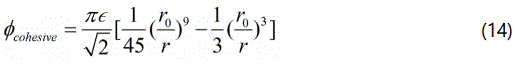
where ϵ is the depth of the potential well, and σ is the distance at which the bulk atomistic potential is zero. r₀ is the equilibrium bond distance in the bulk materials. In this way, the cohesive zone in the multi scale CZM is constitutively consistent with the bulk materials.

This work is unique in providing a completely different approach to find constitutive relations for cohesive zone. And this CZM could be validated by results from molecular dynamics (MD) simulations [15] of crack propagation under high-speed impact. Most strikingly, this model is capable of simulating strong discontinuities across a solid at nano scale, such as micro-cracks and dislocations at small scales. Since the basic principles of colloidal physics and surface chemistry are used to determine the interface cohesive force and the underneath atomistic structure is considered to construct surface or interface cohesive laws.

First Principle assisted Development of Cohesive Law

A key issue to apply a CZM is to determine the values of cohesive parameter, such as at least work of separation, cohesive strength, cohesive length and the coupling between the various modes. In the present literature, many techniques are seen, either fitting to experiments, deriving from a physical model like MD simulation, meso-scale homogenization formulation or multi-scale approaches. And a direct calculation or experimental measurement of a cohesive constitutive relation and parameters seems difficult, if not impossible. Several studies have already suggested that, an ideal cohesive analysis would be based on the interface cohesive potential that is linked to the atomistic potential obtained from first principle calculations [10], and an accurate cohesive zone model should capture the characteristics of atomic-level bond breaking between adjacent atomic layers of a crystal [16,17].

Toward this target, Guo et al. [18] recently performed first-principle (FP) calculations of mixed-mode mechanical responses of a Ni/Al₂O₃ interface in thermal barrier coatings, in order to investigate the spallation and de lamination of the coatings. The authors presented a special discussion on the development of interface cohesive potential that is used to construct the cohesive laws.

First-principle calculation results
The simulation super cell of Ni/Al₂O₃ employed by the authors involves two blocks, namely, Ni block and Al₂O₃ block, see figure 1. The Ni block translates by a displacement (r, δ) relative to the Al₂O₃ block, where r is the horizontal shift of Ni block relative to the Al₂O₃ block along the <110> or <112> direction of the Ni lattice, and δ is the opening displacement of two blocks. The loading angle φ is defined as, tan φ=δ/r. The authors considered three loading orientations of 22.5, 45 and 67.5° with respect to the interface.

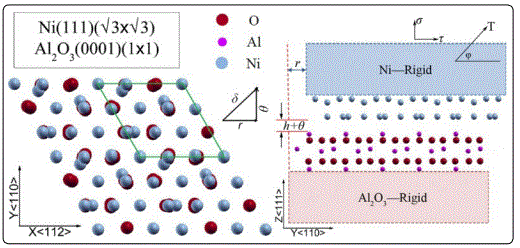
Their FP simulations predict the variations in the tensile and shear stresses with respect to the tensile and shear displacements along different loading angles. The results show that tensile stress–displacement curves are insensitive to the mixed-mode loading angle, and the tension has a substantial effect on the shear strength. Also, interfacial potential energy Ψ and unstable stacking energy γ_us are calculated from this FP study. Ψ is much insensitive to the loading angle under mixed-mode loading. The maximum value of γus decreases as the mixed-mode loading angle increases. Since γ_us is the energy barrier to be overcome in the block-like shear of one-half of a crystal relative to the other, it measures the resistance to sliding of the Ni/Al₂O₃ interface [19]. These mechanical properties are useful in formulating a cohesive law of the interface.

Failure mechanism
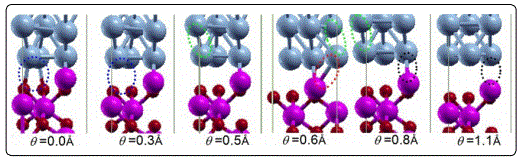
The unique output of this FP study is the evolution of interfacial atomic bonds during loading process, which is a direct evidence of failure mechanism. Figure 2 shows a series of snapshot for notable changes in atomic bonds during the mixed-mode loading process for <110> slip cases. The early breakage of the weaker Ni-O bonds (blue ring) is observed at θ=0.3 Å for all loading angles. With the further increase of the applied load, the new Al-Ni bond (red ring)emerges leading to appearance of two Al-Ni bonds (red and black rings) in the interface. After one of the Al-Ni bonds breaks, the other Al-Ni bonds across the interface break at a critical tensile displacement. The generation of a new Al–Ni bond and the premature breakage of one Al–Ni bond have effectively delayed the final failure of the Ni/Al₂O₃ interface. In addition, the failure of this interface under any mixed-mode loading case takes place by breaking the Al–Ni bond in a ductile fracturing manner. It should be noted that the tensile displacement θ exceeds 0.5 Å, as shown in figure 2, the atomic rearrangement of two Ni atomic layers (green ring) near the interface occurs distinctly, coupling with the formation of the new Al–Ni bond near the interface.

Development of the potential function
Sun et al. [20] conducted a pioneering work about the potential energy Ψ, and suggested an analytical form of Ψ for the combined opening and slip displacements between two atomic planes with an initial separation h. Based on this work, Guo et al. [18] derived the following formulation for Ψ(r, θ) for the <110> slip case

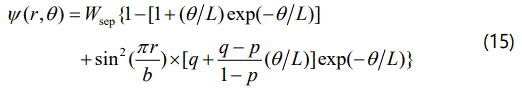
and for the <112> slip case

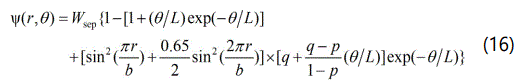
where W_sep is the work of separation for cleaving the two blocks, b is the length of Burgers vector, L is the characteristic length of the de cohesion process, and the parameters p and q are the two dimensionless material parameters that quantify the extent of tension-shear coupling. The potential energy function Ψ(r, θ) is related to stress components through its derivatives as follows

After checking the variations in the tensile and shear stresses obtained from Eq. (17) with respect to the tensile and shear displacements, the authors found that the analytical expression (17) is able to reasonably reproduce the peak tensile stresses in terms of magnitudes for the cases of loading angle 45 and 67.5°, but not for the case of 22.5°. Moreover, Eq. (17) does not fully reproduce the shear stress– displacement curves for the different loading angles. In addition, the derived shear strengths are overestimated to some extent. Both the derived shear strengths and the critical shear displacements increase with the increase of loading angle, indicating the opposite tendency of first-principle calculations.

The divergence between the analytically derived and first-principle calculated stresses–displacement relationships might come from two aspects: (i) a pronounced relaxation effect observed in the mixed-mode first-principle calculations was fully neglected in the calculations of Sun et al. (ii) the analytical potentials might not fully consider the particular physical phenomena found in first principle study, such as, re configuration of Ni atomic layers, generation of a new Al–Ni bond. That is, a linkage between the interface cohesive potential to its first principles awaits further effort. This work demonstrates that first-principle electronic calculation, as the ideal and ultimate solution way to extract a cohesive law, is promising in spite of great complexity.

A Non-Local CZM Accounting Failure Mechanisms

Compared to first-principle method, MD simulations are more favorable in establishing a relationship between CZMs and the physics governing crack formation. However, Paggi and Wriggers [11,12] state briefly that several problems still remain largely unsolved for MD simulations. Instead, they resort back to a continuum damage mechanics formulation, since both CZMs and damage mechanics are routinely used to model complex phenomena of progressive damage eventually leading to fracture. The nonlocal CZM proposed [11,12] takes into account the properties of finite thickness interfaces, and its traction–separation relation considers the complex failure phenomena affecting the material microstructure of the interface region.

Proposals to the nonlocal CZM
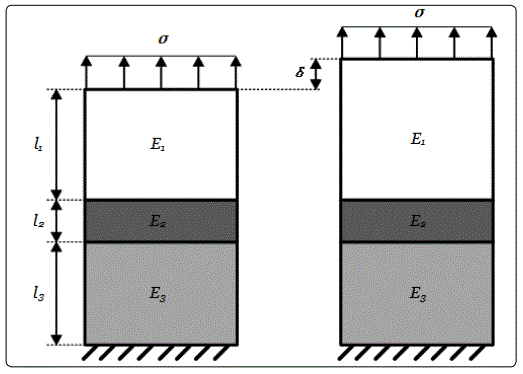
A tri-material system is considered as an example to explain their model, figure 3, in which two bi-material interfaces are perfectly bonded, and the specimen is subjected to uni axial tension in vertical direction.

The loading process has three different stages. In the first stage, the materials deform linearly, and the total axial displacement δ is the sum of all materials

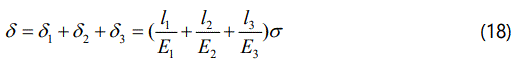
This relation holds until the axial deformation of layer 2 reaches a certain value, δ_e, after which the progressive damage develops in material 2 as a result of lower length scale dissipative mechanisms, such as dislocation motion, breaking of inter-atomic bonds and micro-voids. Thus, a damage variable D is introduced, ranging from zero (δ₂=δ_e) to unity (δ₂=δ_c, full damage of material 2). Hence, the global traction-displacement relation becomes

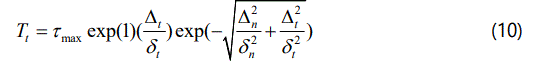
Eq. (19) can be recast by introducing the increment of axial displacement, g_N, with respect to the undamaged case

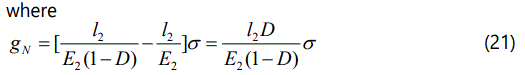
To define the evolution of the damage variable, D is set to the ratio between the increment of deformation from the undamaged case, w=(δ₂-δ_e), and its critical value corresponding to crack formation, w_c=(δ_c-δ_e), raised to a power α

The variables δ_e, δ_c and α depend on damage mechanisms taking place at the lower scales. From Eqs. (20)-(22), the authors have

where w/w_c ∈[0, 1], δ_c=k_Nδ_e, and σ_e=E₂δ_e/l₂ is the stress corresponding to the onset of damage. This equation determines the relation σ=f(g_N) between stress and an-elastic displacement of the mechanical system.

The authors reinterpreted the traction-displacement relation, σ=f(g_N), as a new cohesive traction-displacement law whose shape is no longer assumed a priori.

For this tri-material system subject to shear, damage variable D is defined as

Where u = |ψ₂|-ψ_e and u_c = (ψ_c - ψ_e), ψ_e and ψ_c area threshold and critical values of horizontal displacement of layer 2, respectively. The relation between tangential traction and an-elastic displacement, τ=f(g_T), is determined to be

For the mixed-mode condition, an effective dimensionless opening displacement λ is introduced,

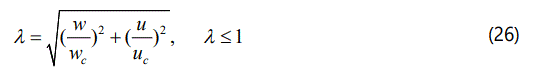
Damage is equal to D=λ^α and the tractions are given by

By increasing the exponent α the response surface of the nonlocal CZM for mode mixity become smoother.

The validity of this nonlocal CZM is verified by comparing with a MD simulation of a mixed-mode crack propagation into Tungsten, which says that the true σ-f(g_N) constitutive equation of the interface is independent of l₁. This work can be regarded as a kind of self-redemption of continuum mechanics for fracture analysis, and continuum damage mechanics formulation was taken to determine the cohesive laws, see Eq. (23) and Eq.(25). They truly recovered several shapes of CZMs used today, such as linear, bi-linear CZMs and also linear softening cohesive law. By tradition, damage mechanics and nonlinear fracture mechanics are totally independent from the mathematical and the engineering viewpoints, and this work bridged this gap nicely. Quite possibly, this method is also applicable to more complicated fracture problems.

Discussions

Cohesive fracture formulations are frequently used to address a variety of complicated phenomena related to damage, cracking and failure of materials, components and structures [21]. However, the simulation accuracy and prediction quality from these analyses should be examined seriously, before giving any guidance or making conclusions in terms of the safety and reliability of the components and structures, or the actual mechanical response of the materials. In recent years, the inherent problems in cohesive zone models are uncovered by researchers, and also many efforts are made to revise them. By reviewing of the main results obtained from the above four groups, some comments and suggestions can be given as below.

Several problems exist in the common cohesive zone models that are widely applied at present. For example, when using the well-known Xu-Needleman CZM of exponential type [22], it may predict an unphysical response of tractions and displacements under mixed-mode separation and over-closure conditions. Most CZMs are applicable for macro-scale material failure analysis in order to fulfill the small scale yielding conditions, and their feasibility cannot be guaranteed when go below sub-micron scale. In other words, they normally suffer from an uncertain range of validity. The shape and input parameters of the CZMs are often chosen as simple as possible for numerical reasons rather than being physically meaningful. In fact, its constitutive parameters may not have a clear physical meaning, and thus are difficult to identify experimentally and to be further verified. By constructing a cohesive law even with the aid of first-principle study, sufficient consideration of mechanical response of material should be taken into, e.g., the relaxation effect, tension-shear coupling and particular physical phenomena during material separation process, in order to provide a physically realistic response from cohesive modelling. And it is somewhat difficult to include all the necessary physics properly, if not impossible.

While there are a great number of CZMs available [22], adequate care should always be taken in performing simulations of fracture. Checking the cohesive law of the model used is a necessity, and if possible, different cohesive laws on simulation results should be systematically and quantitatively investigated. Secondly, when choosing a specific cohesive zone model, one at least has to do, either fitting to experiments, or deriving from a physical model of the fracture process, or directly determination of the cohesive parameters, instead of simply assuming a set of the parameter values. Since cohesive modelling is only a phenomenological continuum approach where no fundamental physics are built in, although it was initiated from a concept of atomistic decohesion and the defect process zone of Barrenblatt [1] and Dugdale [2]. Thirdly, given a cohesive relation between traction and separation, attention should be paid to its capabilities, performance, and limitations under the cases to be investigated, in terms of loading condition, material type, main feature of the mechanical response, and more importantly, inclusion of the key nonlinear processes and dissipative mechanisms. Here, a good example is the work of Mc Garry et al [9], where each of the four newly proposed CZMs has its merits and is suitable in certain case.

As commented by several studies, an ideal cohesive analysis would be based on the interface cohesive potential that is linked to the atomistic potential obtained from first principle calculations [10], and an accurate cohesive zone model should capture the characteristics of atomic-level bond breaking between adjacent atomic layers of a crystal [16]. This suggests the ultimate replacement to the empirical cohesive potential approach. While the current first-principles electronic calculations are still confined in a small range of space and time scales [18,19], one can rely upon alternative ways such as atomistic scale molecular dynamics [23], discrete dislocation dynamics, meso-scale homogenization treatment [24], coarse graining methodology in colloidal physics [10], or emerging multi-scale approaches [25].

Last but not least, cohesive zone modelling is just one option, and all the above-mentioned methods themselves are similarly useful in studying fracture behavior. For example, to treat fracture of a nano-component with a feature size of, say~50 nm, a direct atomistic simulation would be more efficient than any continuum frameworks including cohesive one. Since there are some arguments about the validity of basic continuity assumption and even the definition of stress at the atomic scale, and so on [26].

Concluding Remarks

According to the recent developments by researchers, some of inherent problems or difficulties in cohesive zone modelling have been solved. New potential-based and non-potential-based CZMs proposed by Mc Garry et al. [9] gives a better performance under mixed-mode conditions, compared to the well-established XN potential-based CZM. And they also proposed several useful non-potential-based cohesive zone formulations, providing valuable guidance for future implementation of CZMs for problems involving mixed-mode separation and over-closure. A multi scale CZM introduced by Zeng and Li [10] made the interface constitutive descriptions genetically consistent with the bulk constitutive relations. The method provides an effective means to describe properties of material in homogeneities such as grain boundaries, bi-material interfaces, and inclusions, etc. To let the fundamental physics built in cohesive modelling, first principle electronic calculation could be the necessary or even ultimate solution, since the characteristics of atomic-level bond breaking between adjacent atomic layers of a crystal could be captured by such kind of cohesive zone laws. And the example provided by Guo et al. [18] showed a promising way to construct an accurate interface cohesive law of this kind. While the current first-principles calculations are still confined in a small range of space and time scales, the approaches such as continuum damage mechanics is also helpful to analyze the complex failure phenomena, at larger material scales. Depends on the failure behavior of materials and components and the nature of the problems of interest, one can refer to these studies in selecting a reasonable constitutive laws of CZMs.

Acknowledgements

This work was partial supported by National Natural Science Foundation of China through Grants No. 11672220.

References

1. Barrenblatt GI. The mathematical theory of equilibrium of cracks in brittle fracture. Advances in Applied Mechanics. 1962; 7: 55–129. doi: 10.1016/S0065-2156(08)70121-2   
2. Dugdale DS. Yielding of steel sheets containing slits. J Mech Phys Solids. 1960; 8(2): 100–104. doi: 10.1016/0022-5096(60)90013-2   
3. Hillerborg A, Mod´eer M, Petersson PE. Analysis of crack formation and crack growth in concrete by means of fracture mechanics. Cem Concr Res. 1976; 6(6):773–782. doi: 10.1016/0008-8846(76)90007-7   
4. Needleman A. A continuum model for void nucleation by inclusion debonding. J Appl Mech. 1987; 54(3): 525–531. doi: 10.1115/1.3173064   
5. Rosakis AJ. Intersonic shear cracks and fault ruptures. Advances in Physics. 2002; 51(4): 1189–1257.   
6. Xu XP, Needleman A. Void nucleation by inclusion debonding in a crystal matrix. Model Simul Mat Sci Eng. 1993; 1(2): 111–132. doi: 10.1088/0965-0393/1/2/001   
7. Yan Y, Shang F. Cohesive zone modeling of interfacial delamination in PZT thin films. Int J Solids Struct. 2009; 46(13): 2739–2749. doi: 10.1016/j.ijsolstr.2009.03.002   
8. Máirtín ÉÓ, Parry G, Beltz GE, McGarry JP. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure–Part II: Finite element applications. J Mech Phys Solids. 2014; 63: 363–385. doi: 10.1016/j.jmps.2013.08.019   
9. McGarry JP, Máirtín ÉÓ, Parry G, Beltz GE. Potential-based and nonpotential-based cohesive zone formulations under mixed-mode separation and over-closure. Part I: Theoretical analysis. J Mech Phys Solids. 2014; 63: 336–362. doi: 10.1016/j.jmps.2013.08.020   
10. Zeng X, Li S. A multiscale cohesive zone model and simulations of fractures. Comput Methods Appl Mech Eng. 2010; 199(9-12): 547–556. doi: 10.1016/j.cma.2009.10.008   
11. Paggi M, Wriggers P. A nonlocal cohesive zone model for finite thickness interfaces–Part I: Mathematical formulation and validation with molecular dynamics. Comput Mater Sci. 2011; 50(5): 1625–1633. doi: 10.1016/j.commatsci.2010.12.024   
12. Paggi M, Wriggers P. A nonlocal cohesive zone model for finite thickness interfaces–Part II: FE implementation and application to polycrystalline materials. Comput Mater Sci. 2011; 50(5): 1634–1643. doi: 10.1016/j.commatsci.2010.12.021   
13. Van Den Bosch MJ, Schreurs PJG, Geers MGD. An improved description of the exponential Xu and Needleman cohesive zone law for mixed-mode decohesion. Eng Fract Mech. 2006; 73(9): 1220–1234. doi: 10.1016/j.engfracmech.2005.12.006   
14. Derjaguin BV. Analysis of friction and adhesion IV. The theory of the adhesion of small particles. Kolloid Z. 1934; 69: 155–164.   
15. Buehler MJ, Abraham FF, Gao H. Hyperelasticity governs dynamic fracture ata critical length scale. Nature. 2003; 426(6963): 141–146. doi: 10.1038/nature02096   
16. Van der Ven A, Ceder G. The thermodynamics of decohesion. Acta Mater. 2004; 52(5,8): 1223–1235. doi: 10.1016/j.actamat.2003.11.007   
17. Jiang Y, Wei YG, Smith JR, Hutchinson JW, Evans AG. First principles based predictions of the toughness of a metal/oxide interface. Int J Mater Res. 2010; 101(1): 8–15. doi: 10.3139/146.110254   
18. Guo X, Bao Z, Shang F. Mixed-mode mechanical responses of Ni(111)/α-Al₂O₃(0001) interface by first-principle calculations. J Mater Res. 2013; 28: 3018–3028. doi: 10.1557/jmr.2013.294   
19. Guo X, Shang F. Shear strength and sliding behavior of Ni/Al₂O₃ interfaces: A first principle study. J Mater Res. 2012; 27(9): 1237–1244. doi:10.1557/jmr.2012.85   
20. Sun Y, Beltz GE, Rice JR. Estimates from atomic models of tension-shear coupling in dislocation nucleation from a crack tip. Mater Sci Eng A Struct Mater. 1993; 170(1-2): 67–85. doi: 10.1016/0921-5093(93)90370-T   
21. Bazant ZP, Yu Q. Size-effect testing of cohesive fracture parameters and nonuniqueness of work-of-fracture method. J Eng Mech. 2011; 137(8): 580–588.   
22. Chandra N, Li H, Shet C, Ghonem H. Some issues in the application of cohesive zone models for metal-ceramic interfaces. Int J Solids Struct. 2002; 39(10): 2827–2855. doi: 10.1016/S0020-7683(02)00149-X   
23. Yamakov V, Saether E, Phillips DR, Glaessgen EH. Molecular-dynamics simulation-based cohesive zone representation of intergranularfracture processes in aluminum. J Mech Phys Solids. 2006; 54: 1899–1928. doi: 10.1016/j.jmps.2006.03.004   
24. Yao H, Gao H. Multi-scale cohesive laws in hierarchical materials. Int J Solids Struct. 2007; 44(25-26): 8177–8193. doi:10.1016/j.ijsolstr.2007.06.007   
25. Kulkarni MG, Matous K, Geubelle PH. Coupled multi-scale cohesive modeling of failure in heterogeneous adhesives. Int J Numer Meth Eng. 2010; 84(8): 916–946. doi:10.1002/nme.2923   
26. Kitamura T, Hirakata H, Sumigawa T, Shimada T. Fracture nanomechanics. 2^nd Edition. Singapore, Pan Stanford; 2011.