Abstract

This short article briefly discusses some aspects in shock wave studies in recent years, in particular on the difference between gas dynamics and granular flow problems. It compares the relations of oblique shock waves, where weak, strong and detached shock waves can be observed in both gas dynamic and granular conditions. If the upstream Froude number of granular flow becomes infinitely large a granular shock wave would still remain attached and oblique around a wedge angle near 90°, however an attached gas dynamic shock wave is limited by a maximum wedge angle, say, of 30°. On the other hand, the shock standoff distance for a detached granular shock wave tends to become infinitely small with the increase of the upstream Froude number since it is associated with the flow height ratio across the shock wave.

Keywords: Shock waves; Gas dynamics; Granular Flows.

Introduction

Shock waves are a typical phenomenon in gas dynamics, and can be commonly observed when a supersonic flow moves around obstacles. The term of “shock waves”, however, may be broadly interpreted when the properties of a flow system undergo discontinuous changes, for example through a hydraulic jump, across a contacting surface of granular media, or by a moving front of snow avalanches. The concept of granular shock waves was early proposed by Savage [1] when he studied a stationary jump upstream of a splitter plate, but more focused studies only started to emerge when Gray et al. [2] showed a series of shock waves for granular flow around various obstacles. The study by Gray & Cui [3] established a theoretical framework for the granular shock wave theory. In particular, the successful generation of the strong oblique shocks in their experiment and computation provided a solid evidence for the oblique shock theory of granular flows. Cui et al. [4] then applied this theory to snow avalanche defence problems in Flateyri, Iceland, and suggested that the classical theory can yield an order of magnitude estimates to the avalanche condition and hence could be of important guidance for designing avalanche defences. In recent years, the study of the granular shock waves has been continuously attracting attentions around the world. The following is intended to highlight a few areas in this respect.

The Oblique Shock Wave Theories

While a gas dynamic flow is characterized by Mach number M=|u|/c, where |u| is the flow speed and c is the sound speed, a granular flow can be analogously characterized by a Froude number, defined by Fr=|u|/ √ghcosζ , where h represents the flow height, ζ is the inclination angle of the slope where granular materials flow down under the gravitational force, and g is the gravitational acceleration.

In gas dynamics, the oblique shock theory around a wedge of deflection angle θ has been well developed, e.g. Anderson [5]. If let M₁ be upstream Mach number, β be the shock angle, the following relation can be given

In granular flows, a theory of oblique shock waves was established by Gray and Cui (2007) [3]. If let Fr₁ be upstream Froude number, then a relation can be formed as

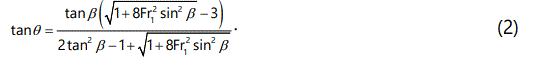
Both equations (1) and (2) can predict the occurrence of weak, strong and detached shock waves based on the deflection angle θ and the upstream Mach number M₁ or Froude number Fr₁. However, distinctive differences also exist between these two theories. First, while a shock wave of gas dynamic flow still follows the energy conservation, the shockwaves in granular flows do not and they are formulated only from the mass and momentum equations of shallowwater type. As a result, the height ratio across a granular shock, say, h₂/h₁ is equivalent to the density ratio, ρ₂/ρ₁, in its gasdynamic term.

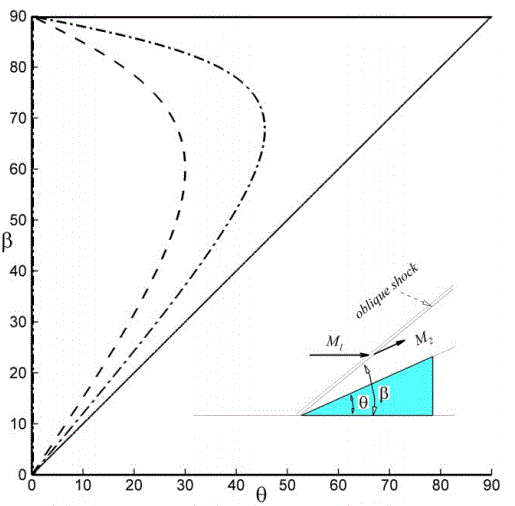
Secondly, there is still an equivalent term of specific heat ratio, γ, in granular flows, and it is equal to 2. However, the granular shock relation of θ – β –Fr₁ is fundamentally different from its gas dynamics counterpart. Figure 1 shows an example of such difference as M₁ or Fr₁→∞, where the dashed line is the result of (1) with γ=1.4, the dash-dot line is the result of (1) with γ=2 and the solid line represents the result for (2). The herein result for the granular flow condition is important since it suggests that, if a granular flow could achieve an extremely high Froude number, the shock formed around a wedge would remain attached and oblique even when the wedge angle θ is close to 90°. On the other hand, there exists a maximum deflection angle θ_max beyond which a shock wave would become detached even as M₁ →∞ according to the gas dynamic relation (1), namely, θ_max=30° if γ =1.4 and θmax=45.58° if γ=2.

Shock Standoff Distance

The standoff distance of shock wave, δ, measures how much detachment a shock wave can form around a blunt body at supersonic speed. Since it determines the exact location of the aerodynamic loading, obtaining an accurate δ is of great importance in aerospace applications. A recent study by Sinclair and Cui [6] provides a good theoretical approximation for gas dynamics flows around circular cylinders, but still shows clear discrepancies when being extended to granular flow problems.

In gas dynamics, it is understood that the shock standoff distance is primarily dependent on the density ratio across the normal section of the shock wave, hence empirical relations for δ have been modelled according to ρ₂/ρ₁, e.g., Lobb [7], Ambrosio & Wortman [8], Olivier [9]. If following a similar approach in granular flow, one would need a density-ratio equivalent term -- flow height ratio, given as [3]

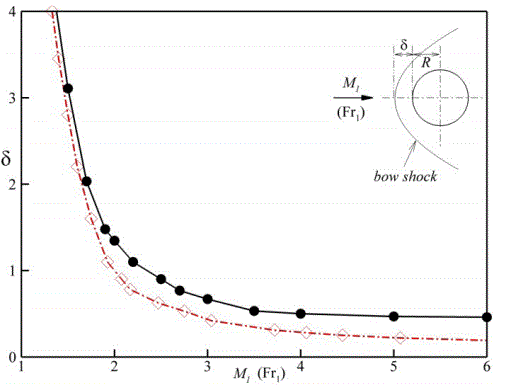
It suggests that the flow height ratio becomes infinitely large as Fr₁→∞, hence the shock standoff distance approaches zero [10]. Figure 2 compares the numerical results of δ for airflow (in circled-solid line) and granular flow [11] (in diamond-dashed line) around a circular cylinder of unit radius (R=1). Clearly, with the increase of Fr₁, δ becomes much smaller for the granular flow problem, implying some fundamental difference for the physics behind gas dynamics and granular flows.

Concluding Remarks

Generally speaking, as flow problems get more complicated the difference between gas dynamics and granular media become more widely disagreed as well. Other typical phenomena to investigate may include the formation and development of the expansion waves, for example, at the rearward side of the obstacle, the granular vacua exhibit distinctive feature in this region [11] but still show much similarity as for the Prandtl-Meyer waves. Also, the shock wave system can develop into a much more complex form if the flow is studied with shock interactions. The study into such problems would not only help to reveal deeper physical insights, but could suggest that more realistic rheological relations would be needed for such granular media.

References

1. Savage SB. Gravity flow of cohesionless granular materials in chute and channels. J Fluid Mech. 1979; 92(1): 53-96. doi: 10.1017/S0022112079000525   
2. Gray JMNT, Tai YC, Noelle S. Shock waves, dead-zones and particle-free regions in rapid granular free-surface flows. J Fluid Mech. 2003; 491: 161-181. doi: 10.1017/S0022112003005317   
3. Gray JMNT, Cui X. Weak, strong and detached oblique shocks in gravitydriven granular free-surface flows. J Fluid Mech. 2007; 579: 113-136. doi: 10.1017/S0022112007004843   
4. Cui X, Gray JMNT, Johannesson T. Deflecting dams and the formation of oblique shocks in snow avalanches at Flateyri, Iceland. J Geophys Res. 2007; 112 (F04012). doi: 10.1029/2006JF000712   
5. Anderson JD. Modern compressible flow. McGraw-Hill, 1982.   
6. Sinclair J, Cui X. A theoretical approximation of the shock standoff distance for supersonic flows around a circular cylinder. Phys Fluids. 2017; 29(2): 0261021. doi: 10.1063/1.4975983   
7. Lobb RK. Experimental measurement of shock detachment distance on spheres fired in air at hyper-velocities. AGARDograph. 1962; 68: 519-527. doi: 10.1016/B978-1-4831-9828-6.50031-X   
8. Ambrosio A, Wortman A. Stagnation-point shock-detachment distance for flow around spheres and cylinders in air. ARS J. 1962; 29(7): 875-875. doi: 10.2514/8.9622   
9. Olivier H. A theoretical model for the shock standoff distance in frozen and equilibrium flows. J Fluid Mech. 2000; 413: 345-353. doi: 10.1017/S0022112000008703   
10. Forbes LK, Schwartz LW. Supercritical flow past blunt bodies in shallow water. Z Angew Math Phys. 1981; 32(3): 314-328. doi: 10.1007/BF00946647   
11. Cui X, Gray JMNT. Gravity-driven granular free-surface flow around a circular cylinder. J Fluid Mech. 2013; 720: 314-337. doi: 10.1017/jfm.2013.42