Abstract

The subject interest of nonlinear unsteady aerodynamics is one of great interest in the aerospace community. The interest is due to the fact that nonlinear unsteady aerodynamic behavior can have a significant effect on the performance and stability of a flight vehicle. To deal with such the aero elastic problem one generally models it by establishing state space equations. In this study, a new technique for determination of transonic nonlinear lift was developed based on discrete reduced-order Volterra series instead of relying on classical approach “eigen system realization algorithm (ERA)”. In this model, one can find out that several time-delayed terms appear. Here we employ Taylor formula to expand these time-delayed terms at the current instant, and then they are vanished. In this study, we also explain how to identify discrete reduced-order kernels. As an example, the two sets of curves between the convolution kernel function method and CFD results match fine.

Keywords: Aero Elastic System; Transonic Flow; Reduced-Order Model; Kernel Function; Taylor Expansion.

Introduction

Aero elastic scholars focus on dynamic stability of the aircraft parts in the air as well as the phenomenon of flutter and dynamic instability [1]. When the flight speed reaches the critical velocity, the interrelation of the unsteady aerodynamic forces, the inertia force and the elastic force may lead to the vibration phenomenon that the amplitude is not attenuated (i.e. flutter), that cause the structure fatigue, damage and even damage [2]. The strong and weak shock wave of wing surface would induce the change of aerodynamic properties in transonic flow, which is the reason for flutter boundary pits and the limit cycle oscillation. Therefore, itʼs essential to study the unsteady and nonlinear transonic aerodynamic properties [3].

The objective of flutter analysis is to search for flutter condition, namely the critical flutter velocity for a given aero elastic system. The nonlinear aero elastic system refers to that either the structure or the aerodynamic force is equipped with the non linear properties or both of them [4]. The structure nonlinearity is roughly divided into the gap nonlinearity, the cubic nonlinearity, the time delay and so on. The flight test of high-aspect-ratio wing at high angle of attack and transonic area nature of nonlinear dynamic need to be studied.

Nowadays, computational fluid dynamics method (CFD) is widely used in the research of nonlinear aerodynamic forces under transonic flows [5,6]. A vast amount of literature on simulation calculations indicates that the CFD method is an economical and effective manner in comparison with wind tunnel tests. Nevertheless, it remains some deficiencies. For example, executing a CFD code is commonly expensive & time-consuming, and huge amounts of calculated data is difficult to be effectively utilized. The technology of identification aerodynamic forces, such as reduced-order models (ROMs), proper orthogonal decomposition (POD), harmonic balance (HB), and neural network method, etc., as an effective alternative was proposed, applied and developed rapidly. Here, our study mainly focuses on ROMs in Volterra theory.

Base on Volterra theory or reduced-order Volterra series [7-10], various nonlinear dynamic forces can be modeled, namely a convolution model, which is suitable only to the given conditions but also to the situations where the experiments would be hard to reach. In Volterra theory, kernels need to be identified by the aid of CFD data. As to the advantage of ROMs in comparison with CFD simulations, it is more effective, but sacrificing accuracy. In ROMs, the reduced-order kernels can be calculated by parametric or nonparametric identification approach. During identification, the required data may come from a flight test or other sources. At present, getting the data by executing a CFD code is a common fashion. However, in ROMs, the discrete time-delayed aerodynamic terms inevitably appear and need to be handled.

In the Establishment of an Aero Elastic System Model section, we describe a 2D wing model and introduce the identification strategy on Volterra seriesʼ discrete kernels method. In the A new technique to deal with transonic timedelayed aerodynamic forces section, a most efficient technique to handle the nonlinear time-delayed aerodynamic forces will be proposed to eliminate those time-delayed terms. By using this new technique, the original aerodynamic model changes into another without time-delayed terms, which is more convenient for various qualitative analyses in comparison with ERA technique. In the Conclusion section, a comprehensive summary of our work is made.

Note that all the results are based on the assumption of a weakly nonlinear aerodynamic system of interest and the small disturbance hypothesis.

Establishment of an Aero Elastic System Model

2D wing structure motion equation (Figure 1)

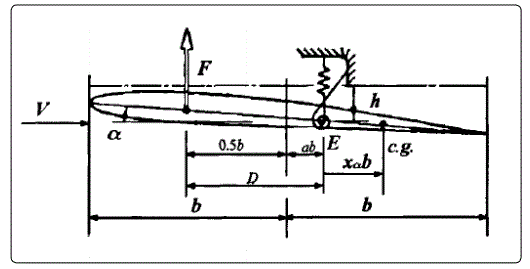
According to Lagrange equation, the matrix form of the wing structure motion equation is as follows:

Where M,C and K denote mass, damping matrix, and stiffness matrices. q, f_a and x = (ξ₁,ξ₂,...ξ_n)^T denote inflow dynamic pressure, generalized aerodynamic coefficient vector, generalized displacement of structure motion.

For ease of analysis, the structural motion equation is usually written in the form of the state equations in the following

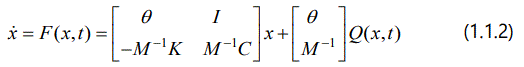
where 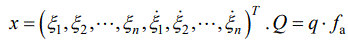is the function of x, t.

Ignoring the damping matrix, the equations of structural motion for the airfoil shown in Figure 1 may be written in the form as

Where m, S_α and I_α denote mass, static pitching moment and rotational inertia about the center of rigidity. K_h and K_α denote pitching spring stiffness and rotational spring stiffness. α And h denote the pitching and plunging displacements about the elastic axis. L And M denote lift and moment.

Using dimensionless time transformation τ = ω_αt, and noting the definitions below:

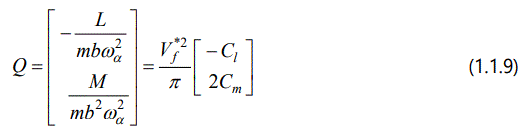
where 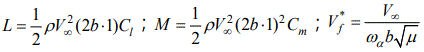;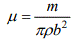. C_l and C_m denote lift coefficient and moment coefficient, respectively. b and x_αb denote the half chord length and the dimensionless distance between the centers of mass and stiffness. r_α ,ω_h and ω_α denote the dimension less rotating radius, the natural frequencies of plunging and pitching modes. μ,ρV_∞ and V^*_f denote mass ratio, density, free-flow velocity, and dimensionless flutter velocity, respectively.

Then, Eq. (1.1.3) can be rewritten as the follows

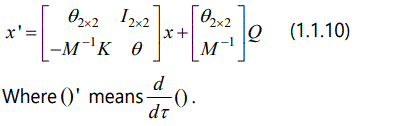
For a nonlinear aeroelastic system, with the increasing of free-flow velocity V_∞ , various adverse aero elastic phenomena may be induced, such as limit cycle oscillation (LCO), chaotic motion and so on.

A simplified model of transonic reduced-order aerodynamic forces
Different from subsonic aerodynamics, transonic flow is inherently nonlinear and involves the production of shock waves. Under transonic flows, high-precise simulation calculations have to be carried out by means of various nonlinear governing equations, especially Navier-Stokes equations. Nowadays, CFD becomes research hotspot in numerical simulation calculations. The disadvantage is that it requires significant time-consuming and massive storage space. As an alternative, the identification technology of unsteady aero dynamic forces shows a high efficient and accuracy for solving transonic aero elastic problems. These technologies include aerodynamic identification of neural network, Volterra series and POD technologies, etc.

In transonic flow, the nonlinear aero dynamic forces can be expressed by Volterra series on the basis of the Volterra theory. Based on the assumption of transonic small disturbance, the weakly nonlinear aerodynamic forces can be modeled by a reduced-order Volterra series as follows [3]:

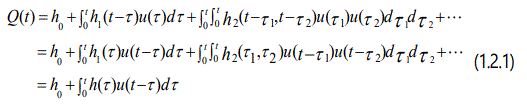
Its discrete form is

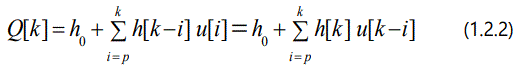
where, h₀ is steady-state solution of steady aerodynamic forces. h₁ and h₂ are the first-order and second-order kernels of the resulting system, respectively. h is called the reduced-order kernel function or equivalent linear kernel function. The expression among the actual time-invariance t , discrete-time step k and sampling time ∆t is t = k∆t, k = 1, 2,3... p is a constant of the system and k - p + 1 denotes the system memory length. u is the arbitrary input, for example: motion displacement.

For a weakly nonlinear system, with the aid of CFD technology (obtaining the required response data for the identification of reduced-order kernels), the formulation of identification of reduced-kernels is given here as the follows [11,12]:

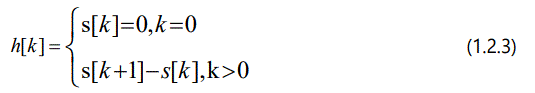
where s[k] represents the system step response; k is called discrete time step; and t = k∆t, ∆t is sampling time.

Sometimes, we hope to improve identification precision of the aerodynamic forces. In this case, one can model them by a reduced-order Volterra series as follows [3]:

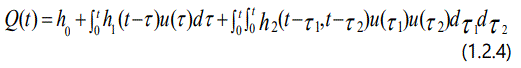
For the sake of convenience, this study mainly focuses on the time-delayed terms of Eq.1.2.2. In the next section, we will propose a new technique to eliminate them and obtain its approximately equivalent form of Eq.1.2.2.

A New Technique to deal with Transonic Time-delayed Aerodynamic Forces

In this section, a new technique is proposed to deal with the time-delayed aerodynamic forces. It is based on Taylor series expansion. Before proceeding further, let us briefly review the most common method, eigen system realization algorithm [13-15] (ERA).

At present, the most popular methodology to study aero elastic stability problems is to establish aero elastic system state equations [16]. How to transform the aerodynamic expression of Volterra series to state-space equations are the key techniques. ERA meets the requirement and has been widely developed since 1985 [13].

Classical eigen system realization algorithm (ERA)
Consider a linear dynamics system represented in statespace form at discrete times t = k∆t, k = , 1, 2,3...with a constant sampling time ∆t, as

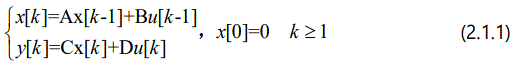
where x[k] ∈ R^n×1 denotes an n-dimensional state vector; state matrix A ∈ R^n×n; input matrix B ∈ R^n×r; output matrix C ∈ R^m×n; and feed-through matrix D ∈R^m×n completely define a linear dynamic system with anr-dimensional forcing function, u[k] , and m-dimensional output measurement, y[k].

It is a well-known fact that Eq. (2.1.1) is equivalent to the Volterra series expression as the following

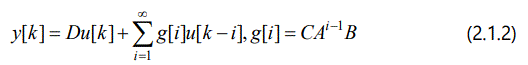
where g[i],i = 1, 2,... denote the Markov parameters and the k indicates the input and output samples at discrete times t = k∆t . Given the input u[k] and output y[k] , the objective is to determine the appropriate size n (McMillan degree) of the state vector x[k] in Eq.(2.1.1), and to estimate a discrete time state-space realization (A,B,C,D) of the dynamic system considered.

From the above description, the whole process needs to be done in two steps: 1) Volterra kernels identification, namely Markov parameters g(i) identification; 2) Modal parameters identification, namely the minimal realization of (A,B,C,D). For decades, ERA is still much to be improved, such as selection of the excitation signal, error controlling and so on. Of course the crux of the problem lies in the aerodynamic problem of how to handle time-delayed aerodynamic forces.

In the “A new processing technique based on Taylor series expansion” section, a new processing method to handle nonlinear time-delayed aerodynamic forces will be proposed. This is an effective and convenient approach more suitable applying to various qualitative analyses.

A new processing technique based on Taylor series expansion
In this section, based on transonic small disturbance theory and the assumption of a weakly nonlinear aerodynamic system, a new processing technique to eliminate the time-delayed aerodynamic forces is now proposed in details which is more convenient for various qualitative analyses in comparison with ERA technique.

According to the Eq. (1.2.2), transonic aerodynamic expression contains time-delayed components. Let the memory length of the system be, for example, k p + 1 = 21, then Eq. (1.2.2) can be rewritten as

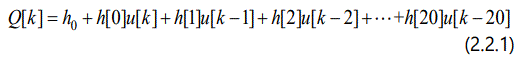
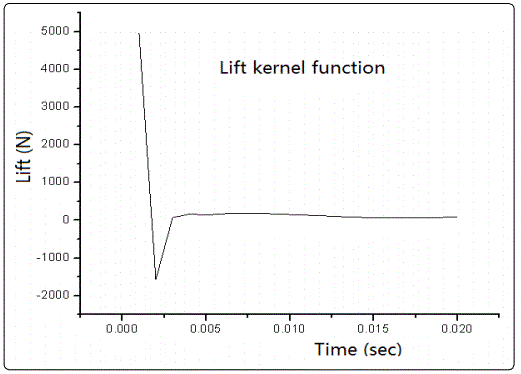
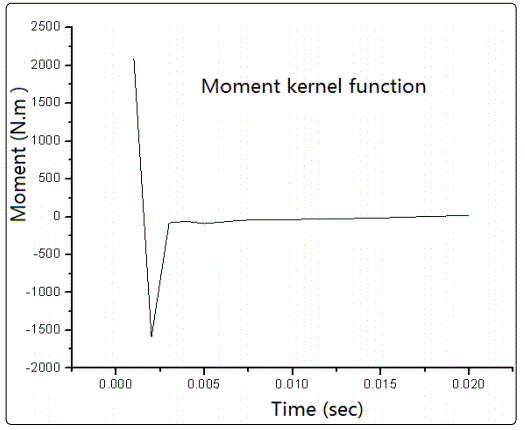
Figure 2 shows the plot of the reduced first-order kernels of lift and moment for a pitching motion in Mach number 0.755 based on Eq. (1.2.3). The time step of a CFD code is ∆t = 0.001 second and the selected memory length k - p + 1 = 21 is reasonable. Based on the Taylor formula the relationship between u(t) and each u(t-i∆t) can be written as the following

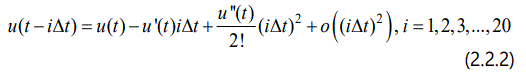
where o(·) is higher order infinitesimal about (i∆t)².

Substituting Eq. (2.2.2) into Eq. (2.2.1), one can see that all the time-delayed aerodynamic terms in Eq. (2.2.1) vanish. Hence, this is a new technique to eliminate the time-delayed aerodynamic terms which have never been mentioned in ROMs before.

Now, let us rewrite Eq. (1.1.3) above. That is shown as follows

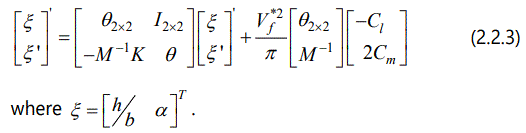
Applying our new technique to the Eq. (2.2.3), the values of C_l and C_m can be replaced by the following expressions

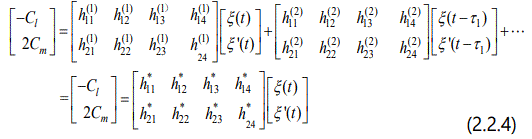
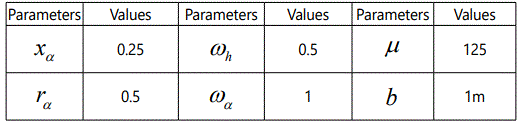
Base on Eq. (1.2.3), and with the help of data provide by executing a CFD code, one can easily identify the values of all the h[k], namely h^(k)_ij shown in the Eq. (2.2.4). Before executing a CFD code, the required structural parameters of 2D airfoil are listed in table 1.

For this pitching motion shown in figure 3, the two curves come from a CFD calculation and the convolution of the first-order kernel with a sinusoidal input y=0.5sin(41.5t), respectively. Here, the frequency of the sinusoidal motion is 41.5 HZ, and the maximum motion amplitude is 0.5 degrees. A good approximation is obtained with the memory length of the 21. This is consistent with the desired result of linearization of a nonlinear system for small amplitudes.

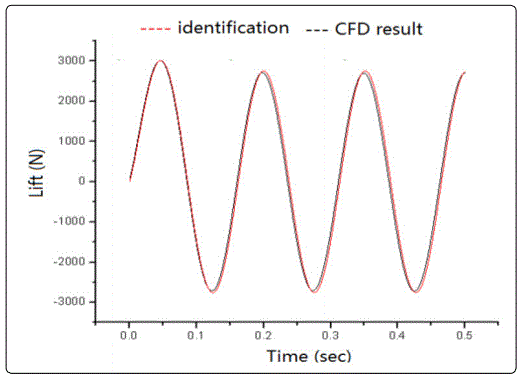
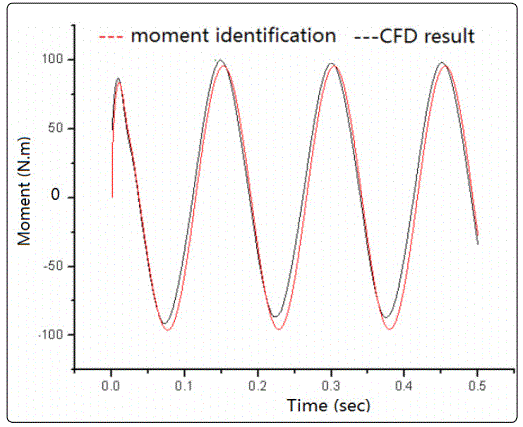
Conclusion

This study modeled the aero elastic flutter equations for a 2D wing, especially aerodynamic reduced-order models based on Volterra series expansion. In this model, one can see some time-delayed aerodynamic terms inevitable appear. For solving it, we propose a new technique to eliminate them which totally differs from the most common technique (ERA). ERA emphasizes how to transform a reduced Volterra Series model into state space model. Our technique emphasizes that if the aerodynamics time-delayed terms vanish, the changed new model of aerodynamic forces can be more convenient for various qualitative analyses.

The main conclusions can be summarized into the following several aspects:

1. Under the transonic small disturbance hypothesis and weakly nonlinear assumptions of aerodynamics forces, based on Taylor series expansion theory, the nonlinear aerodynamic forces can be modeled by the equivalent first-order linear Volterra kernels, by which a nonlinear system can be converted into a linearization system.
2. Based on Taylor expansion, a new technique to eliminate the time-delayed aerodynamics forces is proposed, which is a simple and directly approach more convenient for various qualitative analyses.
3. Due to the short memory length of step or pulse responses of a weekly nonlinear aerodynamic system, Taylor series expansion in this study definitely converges. This shows our technique proposed here is practical and effective.

Acknowledgements

The authors gratefully acknowledge the financial support of the projects of Guizhou Provincial Science and Technology Fund (QKH-JICHU [2017], Grant No. 1408), and the National Natural Science Foundation of China (Grant No. 11302065).

References

1. Dowell E Edward J, Strganac TW. Nonlinear aero-elasticity. Journal of Aircraft. 2003; 40(3): 857-874. doi: 10.2514/2.6876   
2. Anderson JD Jr. Fundamentals of Aerodynamics. In: Aeronautical and aerospace engineering. 5^th edition, McGraw-Hill series; 2001.   
3. Silva WA. Discrete-time linear and nonlinear aerodynamic impulse responses for efficient CFD analyses, PhD dissertation, 1997.   
4. Rugh WJ. Nonlinear System theory: The Volterra/Wiener approach. Johns Hopkins University Press; 1981.   
5. Silva WA, Bartels RE. Development of reduced-order models for aeroelastic analysis and flutterprediction using the CFL3Dv6.0 Code. In: Proceedings of the 43rd Structures, Structural Dynamics and Materials Conference. Denver, Colorado, 2002.   
6. Raveh DE. Identification of CFD-based unsteady aerodynamic models for aeroelastic analysis. AIAA. 2003; doi:10.2514/6.2003-1407   
7. Beran PS, Silva WA. Reduced-order modeling: New approaches for computational physics. In: 39^thAIAA Aerospace Sciences Meeting, Reno, Nevada, 2001.   
8. Beran PS, Lucia DJ, Pettit CL. Reduced-order modelling of limit-cycle oscillation for aeroelastic systems. Journal of Fluids and Structures. 2004; 19(5): 575-590. doi: 10.1016.2004.04.002   
9. Beran PS, Lucia DJ. A reduced order cyclic method for computation of limit cycles, Nonlinear Dynamics. 2005; 39(1-2):143-158.   
10. Balajewicz M, Nitzsche F, Feszty D. Reduced order modeling of nonlinear transonic aerodynamics using a Pruned Volterra Series. In: 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 17th Palm Springs, California, 2009.   
11. Boyd S, Tang YS, Chua LO. Measuring Volterra kernels. IEEE Trans on Circ Syst. 1983; 30(8): 571-577.   
12. Lind R, Prazenica RJ, Brenner MJ. Estimating nonlinearity using Volterra kernels in feedback with linear models. Nonlinear Dynamics. 2005; 39(1-2): 3-23. doi: 10.1007/s11071-005-1906-0   
13. Juang JN, Pappa RS. An Eigen-system realization algorithm for modal parameter identification and model reduction. Journal of Guidance, Control, and Dynamics. 1985; 8(5): 620-627. doi: 10.2514/3.20031   
14. Florea R, Hall KC. Eigen-mode analysis of unsteady flows about air foils. Journal of Computational Physics. 1998. doi: 10.1006/jcph.1998.6102   
15. Dowell EH, Hall KC, Romanowski MC. Eigen mode analysis in unsteady aerodynamics: reduced order models. Applied Mechanical Review. 1997; 50(6): 371-386. doi: 10.1115/1.3101718   
16. Paduart J, Schoukens J, Pintelon R. Nonlinear state space modeling of multivariable systems. In: International Symposium on Nonlinear Theory and its Applications, Bruges, Belgium, 2005; 18-21.