Abstract

One of the phenomenal characteristics of water molecules is associated with its maximum density attribute near 4°C. Such behavior is related to the cluster structure formation around such temperatures, as a result of hydrogen bonding between water molecules. Such phenomenon is crucial for the survival of the marine life at winter time, where ice formation tend to float as a result of their lower density, relative to liquid water. In the current work, the effect of water buoyancy variation upon the whirlpool structure formation is examined in a simulation study, which involves varying the temperature of the wall close to the maximum achievable density by the water molecules. Parameters such as the temperature, pressure, and velocity fields were resolved from the momentum, energy, and continuity governing equation, where the wall temperature were specified as boundary condition to the problem. From the simulation result, it was observed that the direction of the whirlpool swirl changed from the clockwise direction to the counterclockwise direction, as one of the wall boundary temperatures varied from 4°C to 17°C. Such result was affiliated with water buoyancy variation, where a down drift was observed at the section with a higher density. Consequently, two opposing vortices, with different swirl direction, can coexist at the condition pertaining to a maximum density, if the water temperature was close to 4°C, midway between the wall boundaries. Such result can shade light to the dynamics of subsurface vortices formation, as a result of water density variation with temperature.

Keywords: Water; Buoyancy-driven flow; Vortex structures; Whirlpool swirl; Numerical analysis

Introduction

The direct interaction of fluid density variation inside the fluid bulk body causes fluid buoyancy, which is a fundamental feature of natural convection [1-3]. The resulting fluid density is a direct manifestation of the fluid spatial temperature, which induce a fluid stream drift proportional to thermal gradient across the fluid stream [4]. An exception to this fluid behavior is exhibited by the water molecules, which is characterized by peak density near 4 degrees Celsius, as shown in figure 1 [5].

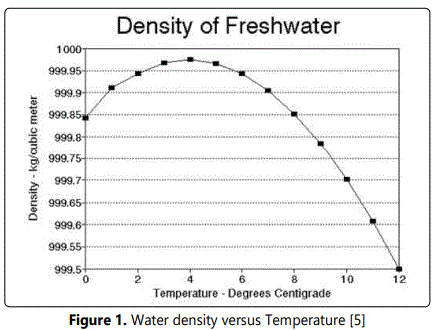
This water intrinsic property is vital for the aquamarine life in the cold seasons, which stratify the lighter ice layers upon the water surface, by buoyancy means. In effect, the aquatic life is preserved in the deep waters, as ice float as a result of its lighter density. Other applications include the magma flow within the earthʼs crust, as a result of temperature variation from the earthʼs core [1, 6-7]. Another peculiar water characteristic associated with buoyancy is the formation of multiple whirlpools of opposing circulation direction, which is the focus of several researches in the past decades. One study examined the water behavior near 4 degrees Celsius under low Rayleigh number condition, where the effect of the fluid bulk convection was considered to be negligible [8]. The study concluded in a qualitative correlation between the various vortex structures and the prevalent buoyancy phenomenon, which was described as a competition between the fluid stream buoyancy and viscous damping from neighboring vortex structures. The effect of buoyancy on the degree of heat transfer was examined in a simulation study by He et al [9], where the velocity profile was observed to have a major impact upon the deterioration of heat transfer. The current study investigates the influence of water density fluctuation upon the vortex formation, where opposing wall boundary temperatures was adapted in the current study, ranging from 4 to 17 degrees Celsius.

Numerical Formulation

The water buoyancy flow was examined using 4 governing equations:

X-Momentum equation

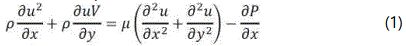
Y-Momentum equation

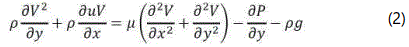
Energy equation

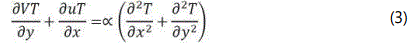
Continuity

In addition, utilizing the B. Gebhart and J. Mollendorf correlation, a fifth equation was used to associate spatial fluid density with temperature, as illustrated in equation 5.

Two non-dimensional numbers were used to characterize the water buoyancy, shown in equations 6 and 7.

Rayleigh number:

Nusselt number:

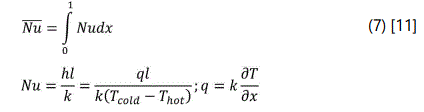
In the numerical Formulation, several assumptions were imposed:

The physical properties of water were treated as a constant value, except in the treatment of buoyancy, where density is subjected to the influence of temperature. Table 1 shows the water properties utilized in the calculation.

The convective terms in both the momentum equation and energy equation were neglected, which can be justified by the Rayleigh number value of the current problem:

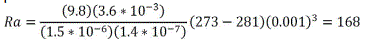
The assessed Rayleigh number is less than the 658 threshold Rayleigh number for water, which is necessary for a significant convection impact [13]. As a consequence, the problem of water buoyancy may be considered as a pure conduction problem. As a result, the governing equation can be rewritten as illustrated in equations 8-10.

X-Momentum equation

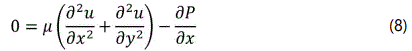
Y-Momentum equation

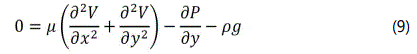
Energy equation

Numerical Procedure

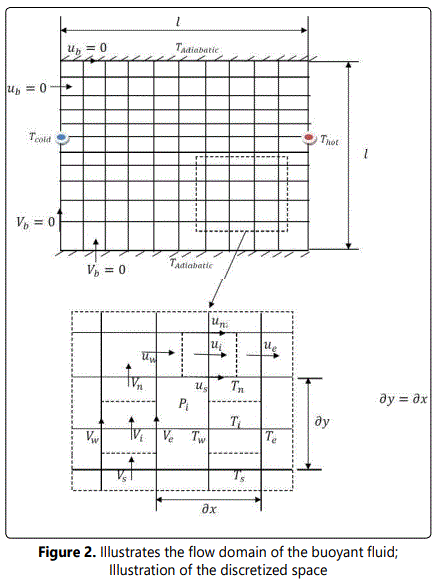
As shown in figure 2, the horizontal and vertical velocity components, Ui and Vi, pertaining to pressure resolution via continuity equation, was solved using the both x-momentum and y-momentum equation, respectively. Other velocity components, such as Vw and Us, were obtained by simply taking the average between the neighboring Vi velocities and Ui velocities, respectively. In the momentum equation discretization, a 3 point Gauss- Seidel was utilized in the numerical procedure, given by equations 11 and 12 [13].

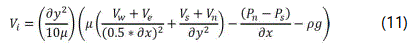
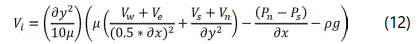
Pe, Pw, Pn, and Ps refer to the pressure gradient across the velocities Ui and Vi. The velocity components along the water enclosure, Ub and Vb, are taken to be zero as a boundary condition treatment to the momentum equations.

The temperature components Ti, associated with fluid buoyancy within the y-momentum equation, were solved using the energy equation, respectively. Other temperature components such as Tw and Ts were obtained by simply taking the average between the neighboring Ti. A three-point Gauss-Seidel was utilized in the numerical discretization of the energy equation, as was the case with the momentum equation.

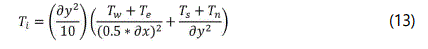
In the boundary condition treatment of the energy equation, an adiabatic condition was applied to the upper and lower sides of the enclosure, as depicted by equation 14.

A thermal gradient was established between low temperature T(cold), and high temperature regime T(hot), along the left and right sides of the enclosure, respectively. T(cold) was fixed at 0°C, while T(hot) was varied from 4°C to 17°C.

The water density associated with buoyancy is resolved using Gebhart and J. Mollendorf correlation, given by equation 5. The correlation constants in equation 5 are:

ω = 9.297173 x10^-6C^-q; = 999.972 kg/m³;
Tw_m = 4.0293°C; q = 1.894816 [3].

In the pressure field treatment, the continuity equation was utilized to ensure mass conservation within the pressure cell vicinity, entailed by equation 15.

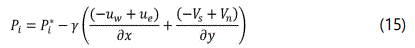
γ in equation 15 is a relaxation factor embedded for solution convergence purposes and P* is the initial or the previous pressure value.

The discretized algebraic equations from the governing equations are solved iteratively starting with an initial guess, where the attained solution from each iteration step is used as the new initial guess for the next iteration procedure.

The residuals at each iteration step are used to monitor the solution convergence, based on equations 16-19.

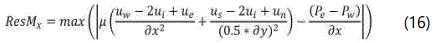
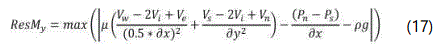
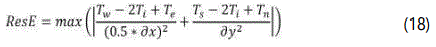
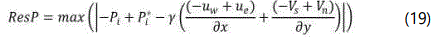
Results:

Discussion

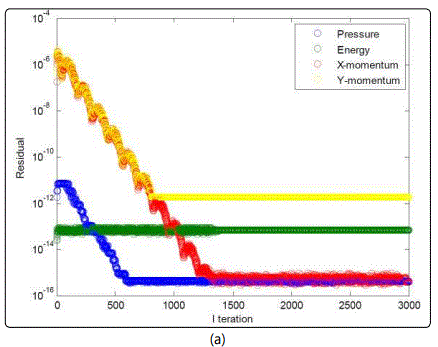
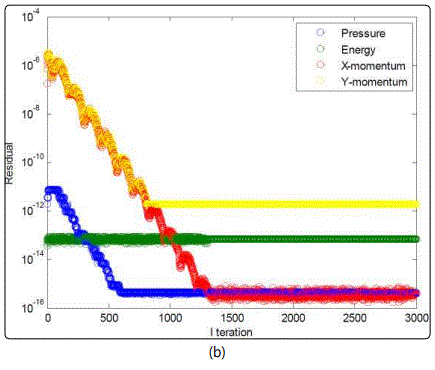
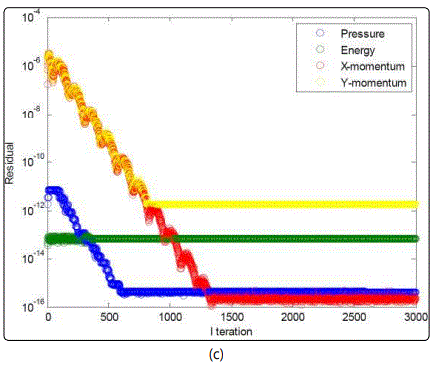
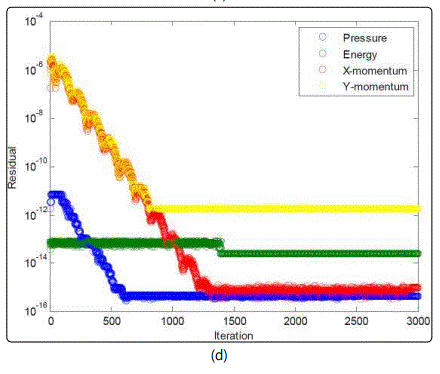
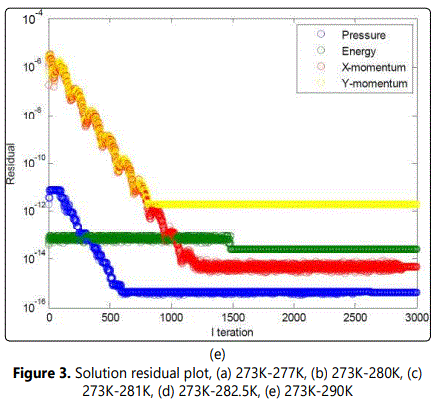
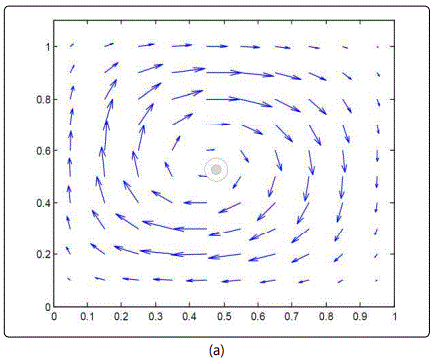
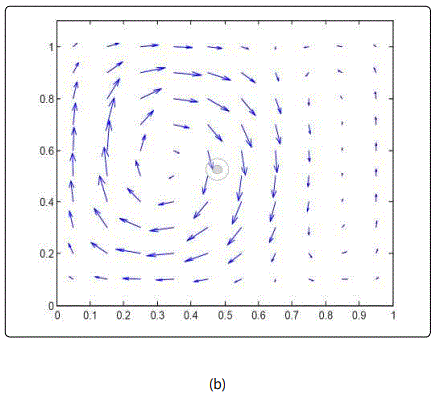
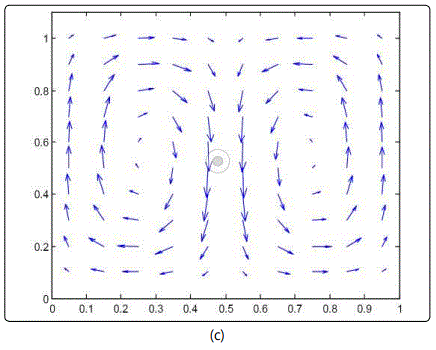
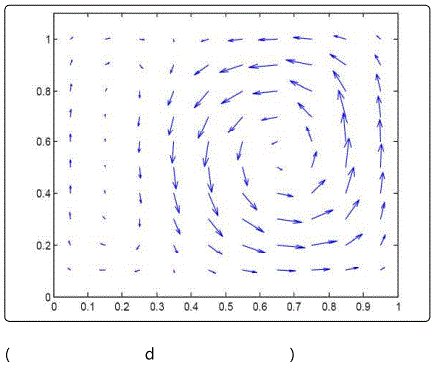
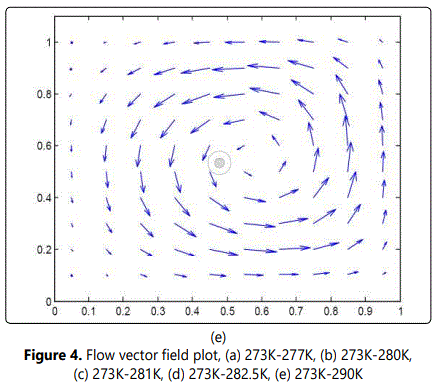
Figure 3 indicate a general solution convergence for the examined range of temperature gradients. One peculiar observation pertains to x-momentum convergence, which spans the largest range of residuals unlike the other governing equations that remain primarily static. Regarding the velocity field depicted in figure 4, a single clockwise vortex is dominant within a temperature gradient between 273K and 277K. Such phenomenon is directly affiliated with the density difference arising from going down the slope from the water maximum density at 277K. An increase in the right boundary temperature crossing the pinnacle density of water brings about the formation of a secondary counterclockwise vortex. This secondary vortex become of equal strength to the clockwise, as the right boundary temperature approaches 281K, further away from the waters maximum density temperature. At this boundary, temperature range water stream arises along both enclosure sides, as a result of the water down drift around the central regime. Further increase of the hotter enclosure boundary escalates the water buoyancy around the counterclockwise vortex, due to the corresponding drop in water density. As a consequence, the clockwise vortex structure is deteriorated under the influence of the anticlockwise increased buoyancy, corresponding to the temperature gradient between 273K and 282.5K. Within the boundary temperature range of 273K to 290K, the degraded clockwise vortex collapses completely as it is overpowered by the lighter anticlockwise circulation. Compared to the other studies in the literature, the average Nusselt number attained from the current numerical simulation was evaluated to be 0.8, which is close to the Nusselt number value acquired by Nansteel et al [8], corresponding to the pure condition case equivalent to 1. With respect to the observed vortex formation, Alawadhi [10] emphasized on the prominent role of wall cooling in driving the flow among different regimes, where a recirculation cell has formed between the cooling wall boundary condition and the adiabatic wall boundary condition. Such result is consistent with the current study, a whirlpool like structure formed between the dissimilar wall condition. Below the maximum water density condition (4°C), Alawadhi [10] described the relation between temperature and density to be of reversed nature, where multiple vortices tend to incur within the simulated envelop. In the current study, a similar result was observed for the case where the wall temperature boundary conditions were above and below the temperature condition, corresponding to the maximum water density. One implication of such result is given by a study of Kandaswamy et al [11], which involves transient natural convection of water within a square enclosure. In Kandaswamy et al study, the heat transfer rate was observed to decrease in the regime with the maximum water density, which is in agreement with the result observed within He et al [9] work.

Conclusion

The water buoyancy near 4 degrees Celsius was examined in a numerical study as a pure conduction heat transfer, based on the formulation of low Rayleigh number. Nusselt number correlation was used to validate the numerical model. One of the prominent results from the study pertains to the influence of buoyancy upon the structure of the circulating vortex. A direct manifestation of the water density characteristics is its potential to generate a double whirlpool with opposing circulation direction, as a result of the water stream down drift around its pinnacle density temperature regime. The size of the formed vortex is directly affiliated with its regimeʼs corresponding temperature, relative to the water maximum density temperature, which hinders the formation of the opposing vortex and lead to its dismissal. One gap area which was not examined in depth in the current study is effect of counter current vortices upon heat transfer, relative to the surrounding regime. Such studies might bring further insight into the dynamics of subsurface interaction within cold water regions.

References

1. Beliaev G M, Brueggeman P L. Deep Sea Ocean Trenches and their Fauna. UC San Diego: Scripps Institution of Oceanography. 1989.   
2. Qiu Y, Zhai H, Zheng Y, Lei G, Wang T, Wang L, et al. Numerical Investigation into the Natural Convection of Cryogenic Supercritical Helium in a Spherical Enclosure. Energies. 2021; 14(9): 2584. doi: 10.3390/en14092584   
3. Nie B, Xu F. Scales of natural convection on a convectively heated vertical wall. Physics of Fluids. 2019; 31(2): 024107. doi: 10.1063/1.5083671   
4. Cianfrini C, Corcione M, Habib E, Quintino A. Natural Convection of Water Near 4°C in a Bottom-cooled Enclosure. Energy Procedia. 2015; 82: 322-327. doi: 10.1016/j.egypro.2015.12.040   
5. Why does water have maximum density at 4 degrees celsius?.   
6. Wirth A. A Guided Tour Through Buoyancy Driven Flows and Mixing. Buoyancy Driven Flows and Mixing, France. 2015; 68   
7. Pugh D T. Tides, Surges and Mean Sea-Level. Chichester, UK: John Wiley & Sons, Ltd; 1987.   
8. Nansteel M, Medjani K, Lin D. Natural convection of water near its density maximum in a rectangular enclosure: Low Rayleigh number calculations. American Institute of Physics, The Physics of Fluids. 1987; 30(2): 312-317. doi: 10.1063/1.866379   
9. He J, Dang C, Hihara E. Theoretical Model for Buoyancy-Induced Heat Transfer Deterioration Under Supercritical Pressure. 17th International Refrigeration and Air Conditioning Conference, Purdue University. 2018.   
10. Alawadhi E. Transient Natural Convection of Water in A Horizontal Circular Enclosure Subjected to Non-uniform Boundary Conditions. The 2nd Joint International Conference on “Sustainable Energy and Environment (SEE 2006). Bangkok, Thailand; 2006.   
11. Kandaswamy P, Sivasankaran S, Nithyadevi N. Buoyancy-driven convection of water near its density maximum with partially active vertical walls. International Journal of Heat and Mass Transfer. 2007; 50(5-6): 942-948. doi: 10.1016/j.ijheatmasstransfer.2006.08.013   
12. Scott P. Thoughts on applicability to our atmosphere.   
13. Winterstein A, Lerch C, Bletzinger K,Wüchner R. Partitioned simulation strategies for fluid–structure–control interaction problems by Gauss– Seidel formulations. Advanced Modeling and Simulation in Engineering Sciences. 2018; 5(29). doi: 10.1186/s40323-018-0123-6