Abstract

The growth rate of ice layer on a surface of the long tube immersed within water medium and containing cold gas flow is considered.

It was determined the layer thickness of ice forming along the tube surface as function of gas follow rate and its initial temperature. The temperature of water medium is above zero.

Keywords: Water ice, heat transfer coefficient, mass gas flow rate, ice thickness, ready made solution, water medium.

Introduction

The math model of heat and mass transfer process under formation water ice on the surface of the tube wall is suggested.

The task is actual for under water works, connected with natural gas, transferred within tube crossing water barriers in winter.

Theory

Let it consider the tube being cooled inside by natural gas, having low temperature t_s = -45°C, water temperature T_w°C has positive level of temperature, its flow velocity donʼt exceed 1 m/s, heat transfer from the side of natural gas is known α_s α_s = 300W/m² s. The tube has no insulation protection, the tube radius is given0,5m, mass flow rate of the gas G_s is 7,7 10⁵ kg/s.

The heat balance differential equation can be expressed in the form

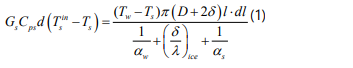
C_ps – specific heat accumulation of gas, Dj/kgK

T_s in, T_s – initial and current temperatures of natural gas glow, K, T_s in =228K

dl – elementary tube length, m

α_w; – heat transfer from the side of water, α_w; = 150W/m²s

G_s – mass rate of natural gas, pumping inside the tube, kg/s

δ – ice thickness, m

λ – heat conductivity of ice, W/mK [1]

D – the tube diameter, m

The aim of this model is to find temperature of gas and ice layer thickness as function of the tube length. To get the result, it is necessary to draw ready made solution, which was made earlier for a case when ice thickness was determined for a flat plate put in to water medium [2]

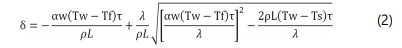
where Tf – temperature of phase changed Tf = 273K
L – heat of phase changes (freezing of water into ice), L=334 103
Dj/kg ρ – ice density, kg/m^w3

If ice thickness is small enough in compare with tube radius, the use of equation (2) justified.

The joint solution of two equations gives the values of the required parameters T_s and δ.

For a long termexploitation of the tube it is of a an interest to estimate maximum ice layer thickness for a certain conditions, this can be described by a stationary – type equation.

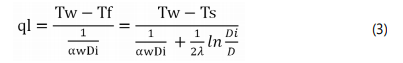
Where T_w – water temperature, T_w =277K T_s – temperature of gas, T_s =228K
ql – density of the heat flux perm, W/m
α_s = 300W/m²K; α_w; = 150 W/m²K
Di – the diameter of the tube-ice composition, m

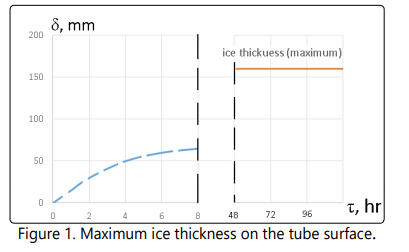
The calculation results are presented on the Figure 1. The dotted line demonstrate the character of the ice layer formation for a short period of the process. The solid line gives maximum ice thickness, m

Conclusion

1. Math model was composed to predict ice layer thickness and gas temperature along the length of the tube being cold from inside by a low temperature gas.
2. The estimation of maximum ice layer thickness, on the tube surface was made.
3. In winter conditions and a long term expluatation of the tube line the thickness of ice layer forming on it may reach the size compared with the tube radius.

References

1. Dean JW, Timmerhaus KD. Thermal Conductivity of Solid O and O at Low Temperatures. Adv. In Cryogen Engineering. 1963; 8: 263-267.
2. Marinyuk BT. The calculation of heat transfer in apparatus and the low – temperature cooling systems. Mashinostroenie. Russia, 2015.