Research Article
Predicting AsphaltenePrecipitation from Heavy Oils Diluted by n-Heptane Using a Four-Parameter EOS
Department of Chemical and Petroleum Engineering, University of Calgary, Calgary, Canada
*Corresponding author: Sajjad Esmaeili, Department of Chemical and Petroleum Engineering, University of Calgary, Calgary, Canada, Tel: (+1)-587-9690662, E-mail: Sajjad.Esmaeili1@ucalgary.ca
Received: March 13, 2018 Accepted: May 14, 2018 Published: May 19, 2018
Citation: Esmaeili S, Maaref S. Predicting Asphaltene Precipitation from Heavy Oils Diluted by n-Heptane Using a Four- Parameter EOS. Int J Petrochem Res. 2018; 2(1): 132-140. doi: 10.18689/ijpr-1000123
Copyright: © 2018 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The aim of this study is to apply the regular solution theory with a liquid-liquid equilibrium to model the asphaltene precipitation and estimate the onset point of asphaltene precipitation for four Canadian bitumens diluted by n-heptane using a four parameter equation of state. The heavy oil/bitumen is characterized in terms of SARA fractions and divided into four different pseudo-components as Saturates, Aromatics, Resins, and Asphaltenes. To calculate the values of solubility parameters, molar volume and density of each SARA fractions, a four-parameter equation of state developed by Adachi et al. is employed for the first time. These properties are required to estimate the onset point of asphaltene precipitation by adding n-heptane solvent to the bitumen.The density calculation of SARA fraction indicates that the average absolute relative error for these bitumens/heavy oils is less than 1.2% and for whole system is about 1%. Furthermore, the results of onset point calculation for different heavy oils demonstrates acceptable predicted values with the average absolute relative error less than about 0.8%. Therefore, the model developed here is found to be successful in fitting and predicting the onset point and amount of asphaltene precipitation which were reported by previous researchers.
Keyword: Asphaltene Precipitation, Onset Point, Regular Solution Theory, Four-Parameter Equation of State.
Introduction
Asphaltenes are defined as the heaviest compounds in the crude oil which can be dissolvedcompletely in aromatic solvents such as toluene, while deposit upon adding paraffinic solventslike n-alkanes [1-8]. Any thermodynamic changes in pressure [9-11], temperature or oil composition, can cause asphaltene precipitation, resulting in many problems in transmission, production, and processing facilities in the oil industry [12-16].
There are large number of experimental techniques such as gravimetric, acoustic resonance [17-19], IFT measurement, dynamic method [20], high-pressure microscopy and infrared spectroscopy [19, 21-23] to detect the asphaletene precipitation. In addition to experimental measurements, a large number of thermodynamic models have been employed to model asphaltene precipitation and predict its onset point, which include solid model [24], micellization model [25], colloidal model [26], solubility model, and equation of state models [27-36].
The solid model is the simplest model for predicting asphaltene precipitation which treats asphaltenes as a single solid component and estimates the behavior of other phases by the equation of state.However, the problem associated with this model is that it needs many empirical parameters and experimental data for tuning [24]. Themicellization model assumes that asphaltene aggregates form with a micelle core coated with resin molecules [25]. The colloidal model which has been introduced by Leontaritis [26], uses a VLE calculation and an EOS to estimate the liquid composition. In this model, asphaltenes are treated as solid colloidal particles which are surrounded by large resin molecules and suspended in the crude oil [37]. In the solubility model on the other hand, asphaltenes are dissolved in a solvent liquid state and creates a uniform solution [9, 38, 39].
Among many thermodynamic approaches employed to predict asphaltene precipitation, the regular solution theory in conjunction with the equation of state models, are the most prevalent techniques [40-43]. It has been confirmed that the regular solution theory can be adapted to the polymerlike system such as solutions composed of solvent/asphaltene [44]. This model uses the solubility parameter or concept of cohesion energy density to describe the asphaltene solubility [40]. Similar to other thermodynamic models, mole fraction, solubility parameters, molecular weight and density of each fraction in the solution are required in this model. Generally, a liquid-liquid equilibrium (LLE) is generated between an asphaltene phase and another liquid phase containing rest of the diluted oil [45]. Hirschberg et al. [2] were the first scholars who employed the regular solution theory to predict the asphaltene precipitated from a crude oil, assuming a single component asphaltene fraction. Later on, it was used to predict the asphaltene precipitation amount and its onset undergoing a composition change [29, 46, 47].
In this study, theHildebrand and Scott [48, 49] regular solution theory is applied to model asphaltene precipitation diluted by adding n-heptane into four different Canadian bitumens with same properties as mentioned by Greaves et al. [50]. Each bitumen is divided into four main pseudo components corresponding to SARA fractions. A four-parameter EOS developed by Adachi et al. [51] is used for the first time to calculate the solubility parameters, molar volumes and densities of SARA fraction. It is notable that the SRK-EOS [52] and the PR-EOS [53] were generally used in previous studies to predict the onset of asphaltene precipitation. However, they required a volume shift term to enhance the accuracy of their liquid density calculations, while this four-parameter equation of state does not require this correction and can yield a better representation of mixture properties. The molar volume and solubility parameters from this four-parameter equation of state are input values in the regular solution model. The outcomes of the developed model are compared with the experimental results as well as the modeling results of previous researches.
Model Description and Methodology
The Four-Parameter Equation of State The four-parameter equation of state has been introduced by Adachi et al. [51] in 1983 to predict the properties of pure substances as well as the mixtures and resolve the deficiency of other two- and three-parameter equation of states in liquid density estimation. Although this equation of state contains four parameters, Adachi et al. have endeavored to keep this equation of state in form of a cubic EOS and involve just one temperature dependent parameter similar to other two- and three-parameter equation of states (i.e. SRK-EOS, PR-EOS and PT-EOS). This four-parameter equation of state is described as below.

where R is gas constant (cm3 .MPa.K-1.mol-1), P is pressure (MPa), T is temperature (K) and V is the fourparameter EOS molar volume (cm3.mol-1). It should be pointed out that this equation of state contains four parameters as a ,b1 , b2 and b3 , where a is a temperature dependent parameter.The definition of each parameter and relevant concepts are mentioned in the Appendix section.
By rearranging Eq. (1) and defining A , B1 , B2 and B3 parameters as a function of operational condition (pressure and temperature), the general cubic form of this fourparameter EOScan be derived based on the z-factor. Therefore, the compressibility factor of SARA fraction can be calculated using Eq. (2).
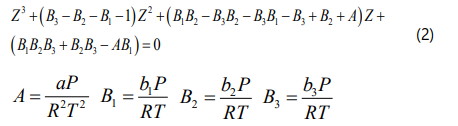
Extension oftheFour-Parameter EOS to Asphaltene Aggregates
As it is known, asphaltenes tend to self-associate and the aggregates can be analogous to polymer-like compounds. It has been shown that asphaltene association can be modeled same as linear polymerization [43, 44, 46, 50, 54, 55]. Since the structure of asphaltene monomers is repeated throughout the structure of asphaltene aggregates, the asphaltene monomers can be considered as a group, for which the Van der Waals forces are involved in the association mechanism instead of chemical bonding. Due to the similar molecular bonding, the critical properties of asphaltene aggregates are same as their monomers. Therefore, four parameters of the Adachi et al. EOS can be used for asphaltene monomers using the group contribution method [50]. By applying the group contribution method on a ,b1 , b2 and b3 parametersof the four-parameter EOS, the modified form of these variables can bederived as follow.




In the above equations,&rmacr; shows an average number of monomers in a given aggregate, which can be calculated based on Eq. (7), and subscript m and a refer to the monomer and aggregate; respectively.

By substituting the modified forms of the four parameters into Eq. (1), the extended four-parameter EOS can be obtained as Eq. (8), which is able to calculate the molar volume of asphaltene aggregate. The general cubic form of the extended four-parameter EOS is also derived by rearranging Eq. (8) based on the Z-factorand presented in Eq. (9).
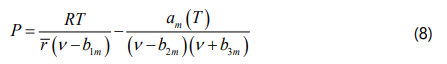
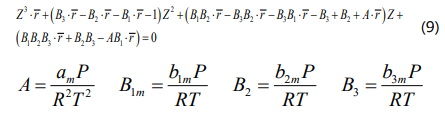
where ν = V/ &rmacr; is the monomer molar volume.To solve Eq. (9), the average number of monomers in each asphaltene aggregate must be determined and we used the reported values by Greaves et al. [50] for the four Canadian bitumens in this study.
a) Asphaltenes+Solids extracted by n-pentane
b) Weight percent of total C5-Asphaltene and Solids
Calculating the Critical Properties of SARA Fraction
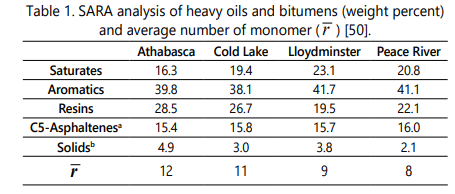
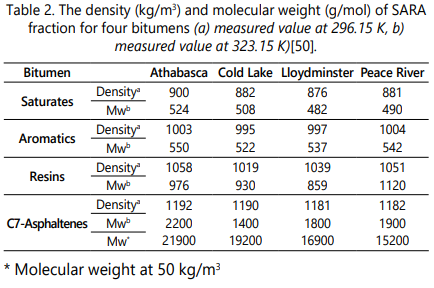
Four bitumens/heavy oils used in this study are categorized into four chemically distinct fractions as Saturates, Aromatics, Resins, and Asphaltenes (SARA analysis). The description of the SARA fraction of the four bitumens including Athabasca, Cold Lake, Lloydminster, and Peace River are presented in Table 1. In addition, the values of molecular weight and measured density for SARA fractions of these bitumens are reported in Table 2 [50].
The first step in employing the four-parameter EOS to calculate the onset of asphaltene precipitation is to estimate the critical properties of SARA fraction including the critical pressure, critical temperature and acentric factor. Based on the previous section, critical properties of asphaltene aggregates are same as their monomers. It is worthwhile noting that the asphaltene fraction is also separated into pseudo-components based on molar mass and the gamma distribution function (ψ(β ) ) is employed for this purpose to describe the molar mass distribution function as shown in Eq.(10). This study discretizes the asphaltene distribution into 35 fractions where the molar mass varies between 1600 and 25000 g/mol. This number of fractions is consistent with previous researches [44, 46, 54-56].
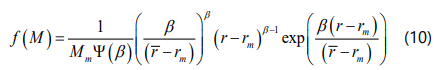
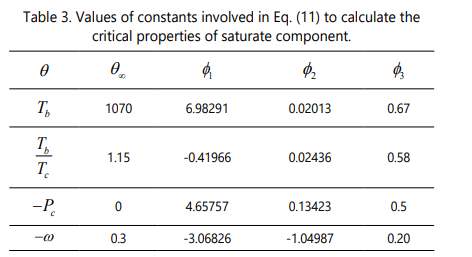
To estimate the critical properties of saturate fraction, an accurate correlation introduced by Riazi and Al-Sahhaf [57] is used as expressed by Eq.(11). This correlation is a function of the saturate compound molecular weight and is able to calculate critical temperature, critical pressure, acentric factor, and boiling point. The four constants of Eq. (11) are expressed in Table 3.
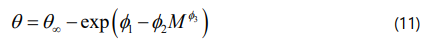
It should be pointed out that a simple and accurate correlation have not been determined yet for the rest of SARA fractions including aromatics, resins and asphaltenes. However, a proper empirical correlation has been proposed by Garnier et al. [58] based on the group contribution method for polynuclear aromatics, which can be used to calculate the critical properites of SARA fraction as a function of molecular weight. Eq. (12) through Eq. (15) show these correlations for the critical temperature, critical pressure, critical volume, and acentric factor of SARA fractions.


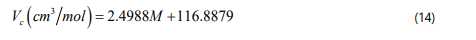

where cf is a correction factor for the acentric factor of aromatic, resin and asphaltene, which is introduced due to the small structural differences between polynuclear compounds and SARA fraction [50, 55]. Note that the correction factor for each SARA fraction can be determined through matching the value of the estimated density to the experimentally measured density, which will be expressed in the following sections.
The Regular Solution Model
To calculate the amount of asphaltene precipitation under the LLE or SLE using the regular solution model, the equilibrium ratio of SARA fractions must be determined, which can be evaluated as Eq. (16).
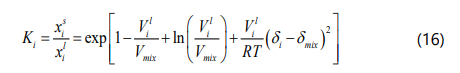
According to the Flory-Huggins theory, the chemical potential of SARA fractions in a bitumen/pure solvent mixture can be calculated by Eq. (17).
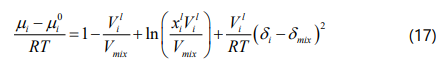
where μi is the chemical potential, xi is the mole fraction, Vi is the liquid molar volume, and δi is the solubility parameter of the ith SARA fraction. Moreover, Vmix and δmix show the liquid molar volume of the bitumen/solvent mixture and the solubility parameter of the bitumen/solvent mixture; respectively.
Hildebrand, Prausnitz, and Scott proposed a liquid solubility parameter for a non-polar solvent as a function of the internal energy of vaporization and the molar volume of the liquid phase, which can be calculated form Eq. (18). Based on the definition of internal energy of vaporization ΔUlv and also calculating the relevant integral, the general form of the solubility parameter for the four-parameter EOS can be derived as Eq. (22).

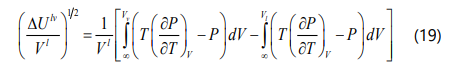
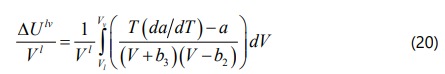
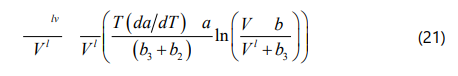
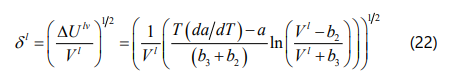
Yang et al. [42] mentioned that if one assumes asphaltene fraction as a pure component, the onset point of asphaltene precipitation can be determined by satisfying Eq. (23). If we substitute Eq. (23) into Eq. (17), the onset point of asphaltene precipitation can be determined when the F coefficient in Eq. (24) is zero.

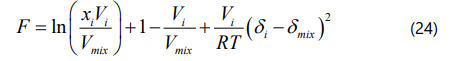
Based on Eq. (24), a negative value of F is known as a stable condition of asphaltene in the bitumen/pure solvent mixture, while a positive value of F is referred to an unstable condition of asphaltene, which causes asphaltene precipitation. This is a simple approach to determine the onset point of asphaltene precipitation. It should be mentioned that to determine the whole liquid phase properties such as the solubility parameter, molar volume, density, and molecular weight, the mixing rule is utilized as shown in Eq. (25) through Eq. (28).




where, xi denotes the mole fraction, &rhoi is the phase density, wi is the mass fraction of ith SARA fraction, and δmix is the solubility parameter of the bitumen/solvent mixture. It is notable that the value of asphaltene molar volume is Va = &rmacr;?a in these correlations.
Results and Discussions
Model Validation
To validate the model, the estimated values of molar volume and solubility parameters of SARA fractions and a given solvent are compared to the measured or calculated values from literature, which are mentioned in the following subsections. The molecular weight and density of SARA fractions are extracted from Table 2. To calculate the molecular weight of asphaltene, the molar mass distribution of asphaltene is required. In this study, the molar mass of the first asphaltene precipitated from the crude oil is estimated by the trial and error and the approximated value of asphaltene molecular weight is found to be around 1600 g/mol, which is consistent with the existed literature [44, 46, 50, 54, 55, 57, 59]. It is notable that this value is used for all bitumens in this study.
Density calculation
Due to the small structural difference between the polynuclear compounds and the SARA fraction, some critical properties of SARA fraction including the critical pressure, critical temperature and acentric factor can be tuned before the onset point calculation. The acentric correction factor is tuned here by fitting the calculated density to the measured density for each bitumen and the average value is used for each bitumen. The acentric correction factor, calculated density and measured density for each bitumen using the four-parameter EOS are reported in Table 4, which reveals that the relative errors are less than 2%. Moreover, the table demonstrates that the four-parameter EOS without the volume shift term can accurately determine the density of SARA fraction and the whole bitumen. The average values of acentric correction factor for previous studies which employed the PR-EOS and the SRK-EOS was found to be 0.9024, 0.8098, 0.7910 and 0.7940 for Saturate, Aromatic, Resin and Asphaltene; respectively. It is notable that the acentric correction factor obtained in this study are different from the PR-EOS and the SRK-EOS [59] results.
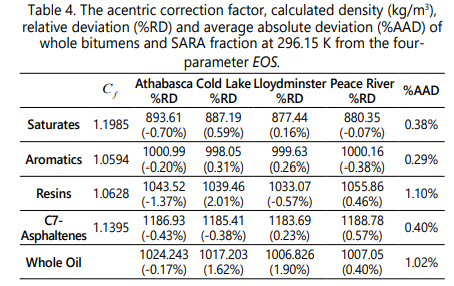
According to the absolute deviation of the density of SARA fraction calculated from the four-parameter EOS in Table 4, this four parameter EOS like the PR-EOS and the SRKEOS is reliable for density calculation of SARA fraction after evaluating the acentric correction factor.
Solubility parameter calculation
In this section, the performance of the four-parameter EOS is examined in prediction of solubility parameters of some pure substances such as n-pentane, n-heptane, n-octane and other substances to confirm its reliability in calculating the onset point and predicting asphaltene precipitation. Prior to calculating the solubility parameter, the acentric correction factors of SARA fraction is tuned based on the previous section and the molecular weight of first asphaltene precipitated of four bitumens is determined as mentioned previously. It should be also pointed out that the liquid molar volume is needed for calculating the solubility parameter.
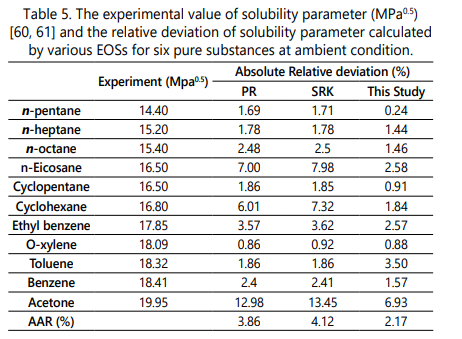
Table 5 compares the experimental [60, 61] and calculated values of solubility parameters for six different pure substances at atmospheric pressure and temperature of 298.15 K. Note that the value of solubility parameters obtained by the PR-EOS and SRK-EOS are reported based on the previous studies [62] and relevant data of the four-parameter EOS is only calculated in this study. To improve the accuracy of liquid molar volume calculation from the PR-EOS and SRK-EOS, the Peneloux volume correction [63] factor is employed. According to Table 5, the four-parameter EOS is more accurate than the PR-EOS and the SRK-EOS in solubility parameter calculation for pure solvents.
Calculating the Onset Point of Asphaltene Precipitation
The onset point of asphaltene precipitation by adding a specific amount of n-heptane to the four bitumens is calculated using the four-parameter EOS at 296.15 K and atmospheric pressure. To determine the onset point of bitumen diluted by n-heptane based on the regular solution theory, the molar volume and solubility parameter of SARA fraction for a given bitumen is calculated firstly using Eq. (8) and Eq.(22). The mole fractions of SARA fraction and pure solvent are then updated by adding a particular mass of n-heptane to the bitumen and the equilibrium ratio of each component is calculated based on Eq. (16). Afterwards, the Rachford-Rice equation is applied assuming that the solid phase is a pure asphaltene substance and the amount of asphaltene precipitation is calculated and the new liquid composition is evaluated. This procedure is repeated until no variation occurs in the amount of asphaltene precipitation. The onset point is then known as the volume of a solvent in which the asphaltene precipitation first occurred.
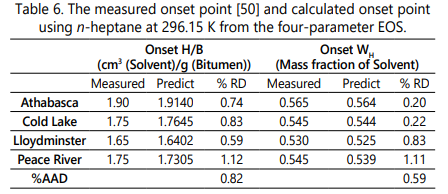
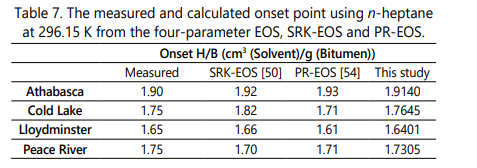
The measured and calculated values of asphaltene onset point for the four bitumens diluted byn-heptane at 23° C and atmospheric pressureare mentioned in Table 6.It should be noted that the measured values in this table are extracted from the study conducted by Greaves et al. [50]. According to Table 6, the four-parameter EOS can accurately estimate the onset point of each bitumen since the deviation values are less than 1.2%. Figure 1 also demonstrates the value of F coefficient versus the dilution ratios in which the zero value of F coefficient occurs at the onset point of asphaltene precipitation. The comparison between the onset point estimation from the SRK-EOS, PR-EOS, and the four-parameter EOS is shown in Table 7. Although the SRK and the PR equation of state can also determine the onset point of each bitumen [50] with considering volume shift and the acentric correction factor, the current research demonstrates that the four-parameter EOS can predict the onset point more accurately due to more reliable density and molar volume calculations and without requiring the Rackett compressibility factor.
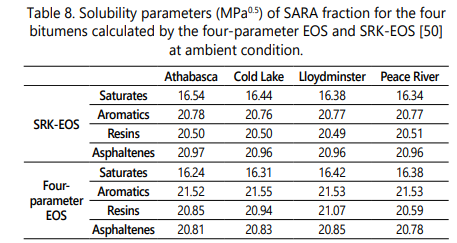
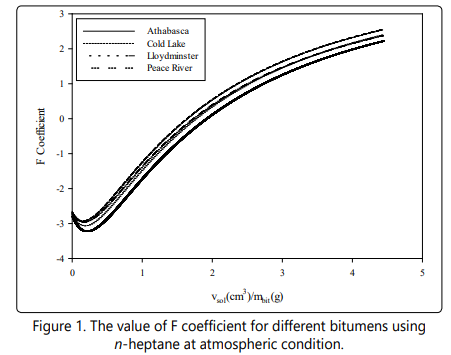
The calculated values of solubility parameters of SARA fractions of four bitumens using the four-parameter EOS in the present study and the SRK-EOS and PR-EOS from the study done by Greaves et al. [50] and Sabbagh et al. [54] are reported in Table 8. The results show that the four-parameter EOS is an appropriate equation of state to be used in the regular solution theory for estimating the asphaltene precipitation onset by adding n-heptane. Figure 2 also reveals the fraction al precipitation of asphaltene for four bitumens using pure n-heptane versus the dilution ratio by applying the four-parameter EOS. According to this figure, the whole asphaltene is expected to be precipitated by adding an infinite volume of solvent to the bitumen.
Conclusion
The performance of a four-parameter equation of statewas examined in the regular solution theory to predict the onset point of asphaltene precipitation diluted by n-heptane. Four Canadian bitumens including the Athabasca, Cold Lake, Lloydminster, and Peace River were characterized in terms of SARA fraction and their molar volumes, densities, and solubility parameters were determined using molecular weight and density data reported by Greaves et al. [50]. To validate the model, the calculated values of molar volume and solubility parameters of SARA fractions were compared with the measured values reported in the previous studies. The results showed that the density and molar volume of SARA fraction for each bitumen as well as the solubility parameter of pure solvents were estimated accurately using the fourparameter equation of state. Using the validated model, the onset point of asphaltene precipitation diluted by n-heptane was calculated for the four Canadian bitumen, which showed great consistency with that previously calculated using the PR- and SRK-EOSs. Moreover, this four-parameter EOS did not need the volume shift expression for correcting the calculated liquid density and it showed more advantageous over the PR-EOS and the SRK-EOS.
Nomenclature
| P | Pressure |
| T | Temperature |
| Vl | Liquid molar volume |
| dH2 | diameter of hydrogen membrane tube (m) |
| b1 | “b1” parameter in EOS |
| “b3” parameter in EOS | |
| B1 | “B1” parameter in PT-EOS |
| B3 | “B3” parameter in PT-EOS |
| r¯ | Average number of monomer |
| M | Molecular weight |
| x | Mole fraction |
| xl | Mole fraction of liquid phase |
| ΔUlv | Internal energy of vaporization |
| R | Gas constant |
| V | Volume |
| a | “a” parameter in EOS |
| b2 | “b2” parameter in EOS |
| “A” parameter in PT-EOS | |
| B2 | “B2” parameter in PT-EOS |
| Z | Gas compressibility factor |
| Mm | Monomer molecular weight |
| Cf | Acentric correction factor |
| xs | Mole fraction of solid phase |
| w | Mass fraction |
| Subscripts | |
| i | ith component |
| c | Critical property |
| m | Monomer |
| mix | Mixture |
| b | Boiling point |
| a | Aggregate property |
| Greek Symbols | |
| ρ | Density |
| ω | Acentric factor |
| λb1 | A coefficient for “b1” parameter |
| λb3 | A coefficient for “b3” parameter |
| β | Shape of distribution function |
| δ | Solubility parameter |
| λa | A coefficient for “a” parameter |
| λb2 | A coefficient for “b2” parameter |
| μ | Chemical potential |
| ψ(β) | Gamma distribution function |
| Abbrevations | |
| EOS | Equation of State |
| VLE | Vapor-Liquid Equilibrium |
| SLE | Solid-Liquid Equilibrium |
| SRK-EOS | Soave-Redlich-Kwong Equation of State |
| AAD | Average Absolute Deviation |
| H/B | Volume of solvent per unit mass of bitumen |
| IFT | Interfacial Tension |
| LLE | Liquid-Liquid Equilibrium |
| PR-EOS | Peng-Robinson Equation of State |
| RD | Relative Deviation |
| WH | Mass fraction of solvent |
Appendix A
The definition of ac, b1, b2 and b3 parameters for the four-parameter EOS are provided as follow.
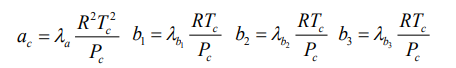
where λa, λb1, λb2 and λb3 can be determined by Eq. (A.1) throughEq. (A.4).

In addition, the following correlations are also required to calculate a parameter in the four-parameter EOS.
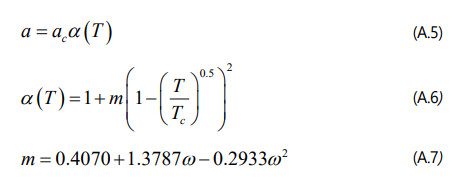
References
- Durand E, et al. Effect of chemical composition on asphaltenes aggregation. Energy Fuels. 2010; 24(2): 1051-1062. doi: 10.1021/ef900599v
- Hirschberg A, et al. Influence of temperature and pressure on asphaltene flocculation. Society of Petroleum Engineers Journal. 1984. 24(03): 283- 293. doi: 10.2118/11202-PA
- Hoepfner MP, et al. A fundamental study of asphaltene deposition. Energy & Fuels. 2013; 27(2): 725-735. doi: 10.1021/ef3017392
- Mehranfar M, et al. Effect of temperature on morphologies of evaporationtriggered asphaltene nanoaggregates. Langmuir. 2014; 30(3): 800-804. doi: 10.1021/la4045896
- Mullins OC, et al. Asphaltenes, heavy oils, and petroleomics. Springer Science & Business Media, 2007.
- Speight J, Petroleum Asphaltenes-Part 1: Asphaltenes, resins and the structure of petroleum. Oil & gas science and technology. 2004; 59(5): 467- 477.
- Speight JG. The chemistry and technology of petroleum. 2014: CRC press.
- Vargas FM, et al. On the development of an enhanced method to predict asphaltene precipitation. Offshore Technology Conference., 2014.
- Burke NE, Hobbs RE, Kashou SF. Measurement and Modeling of Asphaltene Precipitation (includes associated paper 23831). Journal of Petroleum Technology. 1990. 42(11): 1,440-1,446. doi: 10.2118/18273-PA
- De Boer R, et al. Screening of crude oils for asphalt precipitation: theory, practice, and the selection of inhibitors. SPE Production & Facilities. 1995; 10(1): 55-61. doi: 10.2118/24987-PA
- Srivaslava A, et al. Quantification Of Asphaltene Flocculation During Miscible CO Flooding In The Weyburn Reservoir. in Technical Meeting/ Petroleum Conference of The South Saskatchewan Section. 1993. Petroleum Society of Canada.
- Aquino-Olivos A, et al. Investigations of inhibition of asphaltene precipitation at high pressure using bottomhole samples. Energy & fuels. 2001; 15(1): 236-240. doi: 10.1021/ef000136i
- Arciniegas LM, Babadagli T. Asphaltene precipitation, flocculation and deposition during solvent injection at elevated temperatures for heavy oil recovery. Fuel. 2014; 124: 202-211. doi: 10.1016/j.fuel.2014.02.003
- Civan F. Reservoir formation damage. Gulf Professional Publishing. 2015.
- Maqbool T, Srikiratiwong P, Fogler HS. Effect of temperature on the precipitation kinetics of asphaltenes. Energy & Fuels. 2011; 25(2): 694-700. doi: 10.1021/ef101112r
- Mousavi DS, Sefti MV, Mansoori G. Simulation of natural depletion and miscible gas injection effects on asphaltene stability in petroleum reservoir fluids. Petroleum Science and Technology. 2007; 25(11): 1435- 1446. doi: 10.1080/10916460600695264
- Akbarzadeh K, et al. Asphaltenes-problematic but rich in potential. Oilfield Review. 2007; 19(2): 22-43.
- Ali LH, Al-Ghannam KA. Investigations into asphaltenes in heavy crude oils. I. Effect of temperature on precipitation by alkane solvents. Fuel. 1981; 60(11): 1043-1046. doi: 10.1016/0016-2361(81)90047-8
- Jamaluddin A, et al. Laboratory techniques to measure thermodynamic asphaltene instability. Journal of Canadian Petroleum Technology. 2002; 41(7). doi: 10.2118/02-07-04
- Mahmoudi B, Zare-Reisabadi DMR. Experimental study of temperature effect on onset pressure of asphaltene in live oil. Petroleum & Coal. 2015; 57(4): 346-352.
- Abdallah D, et al. Asphaltene Studies in on-shore Abu Dhabi Oil fields, PART II: Investigation and mitigation of asphaltene deposition-a case study. in Abu Dhabi International Petroleum Exhibition and Conference. Society of Petroleum Engineers, 2010.
- Hassanv MB, Shahsavani AA. Study of temperature effect on asphaltene precipitation by visual and quantitative methods. Journal of Petroleum Technology and Alternative Fuels. 2013; 3(2): 1-18. doi: 10.5897/JPTAF11.035
- Zendehboudi S, et al. Asphaltene precipitation and deposition in oil reservoirs–Technical aspects, experimental and hybrid neural network predictive tools. Chemical Engineering Research and Design. 2014; 92(5): 857-875. doi: 10.1016/j.cherd.2013.08.001
- Thomas F, et al. Experimental and theoretical studies of solids precipitation from reservoir fluid. Journal of Canadian Petroleum Technology. 1992; 31(1). doi: 10.2118/92-01-02
- Victorov AI, Firoozabadi A. Thermodynamic micellizatin model of asphaltene precipitation from petroleum fluids. AIChE journal. 1996; 42(6): 1753-1764. doi: 10.1002/aic.690420626
- Leontaritis K, Mansoori GA. Asphaltene flocculation during oil production and processing: A thermodynamic collodial model. in SPE International Symposium on Oilfield Chemistry. Society of Petroleum Engineers. 1987.
- Anderko A. Phase equilibria in aqueous systems from an equation of state based on the chemical approach. Fluid Phase Equilibria. 1991; 65: 89-110. doi: 10.1016/0378-3812(91)87019-6
- Anderko A. Modeling phase equilibria using an equation of state incorporating association. Fluid phase equilibria. 1992; 75: 89-103. doi: 10.1016/0378-3812(92)87009-C
- Anderko A, Prausnitz JM. On the relationship between the equilibrium constants of consecutive association reactions. Fluid phase equilibria. 1994; 95: 59-71. doi: 10.1016/0378-3812(94)80061-8
- Behbahani TJ, et al. Experimental investigation and thermodynamic modeling of asphaltene precipitation. Scientia Iranica. 2011; 18(6): 1384- 1390. doi: 10.1016/j.scient.2011.11.006
- Folas GK et al. Application of the cubic-plus-association (CPA) equation of state to cross-associating systems. Industrial & engineering chemistry research. 2005; 44(10): 3823-3833. doi: 10.1021/ie048832j
- Folas GK, et al. Application of the cubic-plus-association equation of state to mixtures with polar chemicals and high pressures. Industrial & engineering chemistry research. 2006; 45(4): 1516-1526. doi: 10.1021/ ie0509241
- Kontogeorgis GM, et al. Ten years with the CPA (Cubic-Plus-Association) equation of state. Part 1. Pure compounds and self-associating systems. Industrial & engineering chemistry research. 2006; 45(14): 4855-4868. doi: 10.1021/ie051305v
- Oliveira MJ. Coutinho A, Queimada. Mutual solubilities of hydrocarbons and water with the CPA EoS. Fluid Phase Equilibria. 2007; 258(1): 58-66. doi: 10.1016/j.fluid.2007.05.023
- Queimada AJ, et al. Modeling vapor-liquid interfaces with the gradient theory in combination with the CPA equation of state. Fluid Phase Equilibria. 2005; 228-229: 479-485. doi: 10.1016/j.fluid.2004.08.011
- Shirani B, et al. Modeling of asphaltene precipitation utilizing Association Equation of State. Fuel. 2012; 93: 59-66. doi: 10.1016/j.fuel.2011.07.007
- Mansoori GA. Modeling of asphaltene and other heavy organic depositions. Journal of petroleum science and engineering. 1997; 17(1-2): 101-111. doi: 10.1016/S0920-4105(96)00059-9
- Kawanaka S, Park S, Mansoori GA. Organic deposition from reservoir fluids: a thermodynamic predictive technique. SPE Reservoir Engineering. 1991; 6(02): 185-192. doi: 10.2118/17376-PA
- Pfeiffer JP, Saal R. Asphaltic bitumen as colloid system. J. Phys. Chem. 1940. 44(2): 139-149. doi: 10.1021/j150398a001
- Andersen SI, Speight JG. Thermodynamic models for asphaltene solubility and precipitation. Journal of Petroleum Science and Engineering. 1999; 22(1-3): 53-66. doi: 10.1016/S0920-4105(98)00057-6
- Chung TH. Thermodynamic modeling for organic solid precipitation. in SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers. 1992.
- Yang Z, et al. Experimental and modeling studies on the asphaltene precipitation in degassed and gas-injected reservoir oils. Fluid phase equilibria. 1999; 157(1): 143-158. doi: 10.1016/S0378-3812(99)00004-7
- Yarranton HW, Masliyah JH. Molar mass distribution and solubility modeling of asphaltenes. AIChE Journal. 1996. 42(12): 3533-3543. doi: 10.1002/aic.690421222
- Alboudwarej H, et al. Regular solution model for asphaltene precipitation from bitumens and solvents. AIChE Journal. 2003; 49(11): 2948-2956. doi: 10.1002/aic.690491124
- Tharanivasan AK, et al. Measurement and modeling of asphaltene precipitation from crude oil blends. Energy & Fuels. 2009; 23(8): 3971- 3980. doi: 10.1021/ef900150p
- Akbarzadeh K, et al. A generalized regular solution model for asphaltene precipitation from n-alkane diluted heavy oils and bitumens. Fluid Phase Equilibria. 2005; 232(1-2): 159-170. doi: 10.1016/j.fluid.2005.03.029
- Wang J, Brower K, Buckley J. Advances in observation of asphaltene destabilization. in SPE international symposium on oilfield chemistry. 1999.
- Hildebrand J, Scott R. The solubility of nonclectrolytes 3rd edition. New York: Reinhold, 1949. 488.
- Hildebrand JH, Scott RL. Regular solutions.: Prentice-Hall. 1962.
- Greaves M, et al. Estimation of SARA fraction properties with the SRK EOS. Journal of Canadian Petroleum Technology. 2004; 43(9). doi: 10.2118/04- 09-02
- Adachi Y, Lu BCY, Sugie H. A four-parameter equation of state. Fluid Phase Equilibria. 1983; 11(1): 29-48. doi: 10.1016/0378-3812(83)85004-3
- Soave G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chemical Engineering Science. 1972; 27(6): 1197-1203. doi: 10.1016/0009-2509(72)80096-4
- Peng DY, Robinson DB. A new two-constant equation of state. Industrial & Engineering Chemistry Fundamentals. 1976; 15(1): 59-64. doi: 10.1021/ i160057a011
- Sabbagh O, et al. Applying the PR-EoS to asphaltene precipitation from n-alkane diluted heavy oils and bitumens. Energy & fuels. 2006; 20(2): 625-634. doi: 10.1021/ef0502709
- Soroush S, Vafaie Sefti M, Masoudi R. Applying the PR-EOS to predict the onset of asphaltene precipitation from n-alkane diluted bitumens. Iran. J. Chem. Chem. Eng. 2007; 26(3).
- Sabbaghi S, et al. Predicting The Onset of Asphaltene Precipitation by Virial EOS. FDMP: Fluid Dynamics & Materials Processing. 2008; 4(2): 113-124.
- Riazi MR, Al-Sahhaf TA. Physical properties of heavy petroleum fractions and crude oils. Fluid Phase Equilibria. 1996; 117(1-2): 217-224. doi: 10.1016/0378- 3812(95)02956-7
- Garnier S, et al. Modelling solubility of solids in supercritical fluids using fusion properties. Fluid Phase Equilibria. 1999; 158: 491-500. doi: 10.1016/ S0378-3812(99)00151-X
- Akbarzadeh K, et al. Equations lead to asphaltene deposition predictions. Oil & gas journal. 2002; 100(44): 1-51.
- Hansen C. Hansen Solubility Parameters: A Userʼs Handbook CRC. Boca Raton. 2000; 168.
- Kolker A, Korolev V, Batov D. Relationship between the internal pressure and cohesive energy density of liquids. Journal of Structural Chemistry. 2005; 46(5): 927-930.
- Eslamimanesh A, Esmaeilzadeh F. Estimation of solubility parameter by the modified ER equation of state. Fluid Phase Equilibria. 2010; 291(2): 141-150. doi: 10.1016/j.fluid.2009.12.031
- Péneloux A, Rauzy E, Fréze R. A consistent correction for Redlich-KwongSoave volumes. Fluid phase equilibria. 1982; 8(1): 7-23. doi: 10.1016/0378- 3812(82)80002-2



