Abstract

Petroleum resources continue to dominate the energy sectors with no sign of a decline. Petroleum reserves, however, are dwindling in view of fewer new discoveries and increased production level. It is important to determine petroleum reserves accurately in order to correctly forecast energy budget in the future.

The most commonly used methods to describe the fluid flow in oil reservoirs employ constant rock properties. However, these methods are not applicable to reservoirs that undergo changes in the rock properties due to variation in pore pressure. Common characteristics of fractured reservoirs are sensitivity of permeability and porosity to effective stress. The in-situ stress, in itself, can be of mechanical or thermal origin. The thermal stress can be significant in thermal enhanced oil recovery schemes such as injection of cold fluid in hot formation during water flooding or wastewater disposal, or even during hydraulic fracturing.

Unfortunately, the most commonly literature review reveals that the research in this area has been focused mainly on thermal recovery of heavy oil. Few investigation, however, have been done on the onset and propagation of fractures under thermal stress or mechanical stress. Consequently, this paper is devoted to investigate fracture development and propagation in carbonate formation under thermal and mechanical stress. A series of experiments were ingeniously designed to study the effect of thermal stress on fractured carbonate formation. Laboratory experiments were conducted to determine stress-strain relationship and the time dependence taking in account fracture formations and their propagation. A computer image analyzer was used to observe the fracture/fissures distribution for various cases of thermal stress on carbonate rocks. The role of thermal and mechanical stress in determining orientation and propagation of fractures was also studied.

Keywords: Thermal stress Petroleum reserve, Strain, Carbonate rocks, fracture.

Introduction

Transient thermal stresses are of great importance in many applications that deal with large temperature changes. Applications range from the field of microelectronic processes to geothermal processes. In general thermal problems encountered in the field of earth science involve a combination of a solid state and fluid state, whereas in other fields thermal processes deal with microscopically homogenous structures (e.g. manufacturing of mechanical devices).

The study of thermal stress in a homogeneous, isotropic medium started decades ago [1-2] and most of the problems encountered in this area are either amenable to analytical solutions [3] or solved by means of perturbation approach [4]. However, if a body has anisotropic properties, it is more complicated to predict the temperature field and the stresses; numerical method appears to be the method of suitable choice [5].

Wu [6] proposed three different methods to calculate thermal stress. The first is an analytical method that involves an exact solution similar to those encountered in elastic theory. The second method uses the technique of approximations such as the perturbation procedure. Finally, the third method uses numerical techniques to solve the governing partial differential equations.

Even though various forms of semi-analytical methods have been proposed to alleviate the difficulty of large number of grid blocks, numerical methods continue to be common in determining the stress field of a body subjected to thermal stresses. In these cases, the emphasis has been focused on the thermal stress coupled with mechanical stress that originates from pore pressure as well as overburden stress. Gai [7] (2004) summarized some of the salient aspects of Geomechanics modeling and highlighted the need of modeling thermal stress.

Ghassemi [8] showed that rock mechanics research and improved technologies can impact areas related to in-situ stress characterization, initiation and propagation of artificial and natural fractures, and the effects of coupled hydro-thermochemo- mechanical processes on fracture permeability and induced seismicity. Recently, Ghassemi and Tarasovs [9] investigated the development and propagation of system of crack from a cooled wellbore, and secondary thermal cracks in geothermal reservoir due to cold water injection is studied. The extent of the thermal fractures and their spacing is estimated using a combination of the real boundary integral equation method for the temperature solution, and the complex variable boundary integral equation for fracture propagation solution. The results showed that the influence of thermal stress on fractures and their propagation is considered for the problem of sudden cooling of a rock half-space, injection/extraction process in fractures, and cooling of a wellbore.

In a review article, Obembe [10] showed that the subject of heat transfer in oil reservoirs has gained huge attention, due to its diverse range of applications in petroleum reservoir management and thermal recovery for enhanced oil recovery.

Thermal Stress in a Petroleum Reservoir
Most light oil reservoirs in the UAE experienced significant decline in reservoir pressure; therefore there is a great need for initiating pressure-maintenance and/or enhanced oil recovery schemes. UAE reservoirs are mainly carbonate, limestone and dolomite formations that are subject to natural fractures and fissures [11]. However, even when natural fractures are nonexistent within the reservoirs, the use of fluid injection at ambient temperature causes thermal stresses. This can be explained by the fact that the UAE reservoirs are at high temperature (in the neighborhood of 90 C). Furthermore, this phenomenon is applicable to heavy oil reservoirs, which are shallow and constituted of unconsolidated sands when they are subjected to steam or other form heat induction [12]. Consequently, most research activities have focused on determining thermal stress in unconsolidated formations [13] and mechanical strength for unconsolidated formations [14]. Little work has been done in determining thermal stress for deep carbonate formations.

In a thermal recovery techniques study, the thermal stress process is generally not known a priori or only with insufficient accuracy. In the late 80ʼs, however, attempts have been reported in the formulation of the thermal process, Tortike and Farouq Ali [15] presented a formulation in which both thermal and mechanical stresses are considered. Thus, the Tortike and Farouq Ali study can be seen as the first attempt to model subsidence under thermal recovery technique. Unfortunately, the study did not present any solutions to the problems; hence no critical judgment can be made on the formulation.

Interestingly, Chalaturnyk and Scott [16] did not report any effect of thermal stress. For their case of unconsolidated sand, thermal stress may well be negligible as compared to mechanical stress. This is an aspect that has yet to be studied.

In a similar study Chen et al. [17] presented a comprehensive formulation for simultaneously modeling fluid flow and Geomechanics. The study did not include thermal stress and the results were not provided.

Note that temperature changes in the rock induce thermoelastic stresses Hojka et al. [18]. These stresses cause thermal strains that can eventually lead to rupture or shear. The temperature dependency of the thermal stresses can cause enormous variations in the magnitude of the thermo-elastic stresses over a reasonable temperature ranges. Thermal stress is complex and cannot be handled easily, and in general, a multidimensional search problem must be solved, which can be difficult in practice. However, theoretical .estimates of the stresses can be calculated from equations of fluid-saturated, pore-elastic solids by incorporating thermo-elastic rock volume changes. The calculation is straightforward if the effects due to nonlinear deformation module and the elastoplastic processes are neglected.

It is clear from the preceding that the calculation based on both nonlinear deformation and elastoplatic processes may be a demanding problem from the computational point of view. Biot [19] proposed equations for pore-elastic theory, and Schiffman [20] studied the stresses and included the thermal effects into Biotʼs theory. Notice again that the inclusion of the thermal conduction to the original theory was considered to be a difficult task and was only accomplished in the mid 80ʼs [21].

Furthermore, Kurashige [22] reported the first coupling of conduction and convection in the context of thermal stress. Kurashige provided numerical solution for the governing equations. Hojka et al. pointed out that Kurashige work presented inappropriate formulation. They postulated that Kurashige allowed the thermo-elastic stresses to reach the hot fluid front and such action makes the model unrealistic.

Further evidence of the weakness of such model arises from the fact that Kurashige imposed steady-state pressure distribution, leading to poroelastic responses that are not time dependent.

An elaborated technique was performed by Vafai and Sozen [23] to solve the problem. The technique consist of solving the energy balance twice using the approach originally outlined by Chan and Banerjee [24] to solve the energy balance equation with a two-equation model.

This essentially involves solving the energy balance equation with thermal properties of the rock and fluid separately. A heat transfer coefficient was incorporated in order to account for the transfer of energy between the fictitiously separated rock and fluid body. The study demonstrated that there is a lag between fluid and solid temperatures because heat propagation in the fluid is due to convection and conduction whereas the propagation of heat in the solid phase is governed only by conduction.

Hojka et al. derived the transient temperature and stress fields in a two-dimensional domain during constant rate, constant temperature fluid injection. The energy equation was considered to be different for the fluid and the rock. However, the complete conduction equation was not solved for the solid. The procedure consisted of calculating the pore pressure first then the results permitted to evaluate the solid temperature and volume change potentials. Subsequently, rock responses due to thermo-elastic and poroelastic changes were calculated. They re-affirmed the previous observation that the pressure front propagates faster than the thermal front. One of their major findings was that small changes of pressure do not induce large poroelastic stresses; leading them to believe that these effects can be neglected. They observed that the thermoelastic stress changes are limited to the heated or cooled zone in the region between the borehole wall and the injected fluid front. Finally, they demonstrated that shear failure or hydraulic fractures can be initiated on the wall depending mainly on the temperature of the injected fluid.

Dusseault [25] outlined stress changes during a thermal operation. He identified the following effects that make the thermal loading a non-linear problem:

-- Rotation and alteration of principal stress fields;
-- Changes in volume and stress (in magnitude as well as direction);
-- Yield and dilation of the reservoir, leading to changes in absolute and relative permeabilityʼs;
-- Change in overburden and under burden properties due to tensile or compressive cracking or shear yield;
-- Reservoir shearing or overburden cracking due to high pore pressure, thermal stresses, and weakening from yield.
The existence of so many governing parameters and their interactions make the problem intractable. Dusseault suggested that conceptual models be used to aid understanding of the problem before coupling with a reservoir model. He reported a series of configurations for the Geomechanics model, but did not make any effort to couple the model with a fluid flow simulator.

Hojka et al. reported the coupling of convection and conduction for the plane strain borehole. They limited their investigation to single-phase flow. Also, the focus of this investigation was the fluid flow and energy balance equation. No effort was made to couple fluid with Geomechanics modeling.

Stress changes due to temperature: a simple Model Dusseault presented the following simple model of stress changes as function of temperature changes assuming the following:

-- a permeable reservoir at initial stress conditions σ_v1σ_hi, σ_h2, pore pressure u.
-- temperature to principal stresses corresponds to vertical and horizontal directions.
-- linear elastic behavior and Hookʼs Law applies:

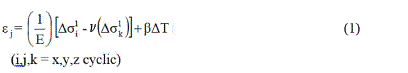
E_i, v and β are Youngʼs modulus, Poissonʼs ratio, and the coefficient of linear thermoplastic expansion. The stress strain law is written in terms of effective stress changes Terzaghiʼs effective stress law is assumed to apply for incremental principal stress changes (∆σ_i):

where α is Biotʼs parameter; α = 1.0 in this analysis. The reservoir is laterally extensive, thus the total vertical stress is approximately unchanged during uniform pressure or temperature changes; ∆σ_v = 0. Assuming a uniform pressure change ∆T = 0), one may show:

Note that stress changes because of injection or production can lead to shearing or tensile yield, depending on initial conditions, Poissonʼs ratio, and the process.

In the more general case, ∆u and ∆T ≠ 0, where u is the internal energy. Using the same boundary conditions and the equations above, one may show:

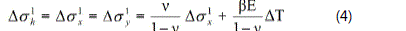
h is a dummy variable.
Note that a temperature change causes a stress change proportional to the stiffness (E), whereas a pore pressure change does not.

This model was adopted by S. Goodarzi et al [26], who simulated CO₂ sequestration and storage.

Objectives
This research is aimed at developing a comprehensive technique for characterizing onset and propagation of fractures in a porous medium under thermal stress. A series of laboratory experiments were conducted, followed by computer image analysis in order to observe the fracture/fissures distribution for various cases of thermal stress on carbonate rocks.

Material and Apparatus

Carbonate Samples
Limestone cores, obtained from outcrops at Hafeet Mountains (Al-Ain, UAE), were used to prepare core samples for porosity and permeability measurements. Two types of cores were used in this study, fractured and no fractured cores. For scanning electron microscope analysis, small sample of each core used in the study were obtained prior to and after thermal shock. The carbonate rocks samples were cut into six small disks 25.4 mm in diameter and 5 mm in thickness.

Scanning Electron Microscope (SEM)
SEM was used in this study to characterize pore size and pore structure of the carbonate samples prior to and after thermal shock. The SEM generates an electron beam from the electron gun. This beam is focused and illuminated on the specimen. As the beam is scanned over the specimen surface in both X and Y directions, secondary electrons back scattered are detected. Amplifying these electron signals and modulating their brightness on the observation cathode ray tube display a specimen image displayed on the cathode ray tube.

Computerized Image Analyzer
A computerized image analysis system was used to study rock samples structure prior to and after thermal shocks. The basic system consists of a high-resolution video camera on an optical microscope, an imager processor, a Pentium PC, a high-resolution image monitor, and a high-resolution text monitor. The image is visualized with the video camera through a microscope lens. As soon as binary images are produced from an accepted microphotograph, a feature count can be performed. Simply selecting the desired bit plane and activating the count option accomplish this objective.

Stress and stain devices
The compressive stress was performed using Conslo type machine WF55205/6, Wykeham Farance Eng. Meanwhile the stress-strain test was performed using Material Testing System (MTS) H20.

Experimental Procedure

Porosity and permeability measurements
Core porosity was measured using the weighing method technique meanwhile liquid permeability method was used to determine core permeability.

Submerging
This method was easy to apply, it consisted of the following:

• Heating the sample until it reaches the requested temperature to make sure that the whole sample (inside and outside) is at the desired temperature we left it in the oven for about 24 hours.
• Preparing a 30°C water in an appropriate quantity and through the sample in it, then wait for 10 - 20 minutes.
• Finally, dry the sample, and then do the liquid permeability measurements using the liquid Permeability Apparatus.

Stress and strain measurements
The experimental study of the effect of thermal shock on stress and strain of lime stone was conducted using nonfractured cores. The study was mainly focused on the compressive stress test and tensile tests. Rocks prior to and after thermal shocks were tested. Microphotos of rock samples were obtained prior to and after thermal shocks using SEM and Image Analyzer System, to investigate and try to observe the creation of any micro-fractures as a result of thermal shock.

Results and Discussion

Effect of thermal shock on cores
Two sets of cores were used to test the effect of thermal shock on rock permeability. The first set consists of four nonfractured cores 1MIS, 2MIS, 3MIS, and 4MIS having the following initial permeably: 0.11, 7.17, 20 and 23.14 respectively. To simulate the temperature shock, the cores were heated at 100 and 150°C for 24 hours to reach the desired temperature. When the heating process reached the set temperature, the cores were taken from the oven and immediately immersed into water at 25°C. Permeability measurements of the cores were performed on the thermally shocked cores. Fig. 1 shows the effect of thermal shock on non-fractured core permeabilityʼs. From Fig. 1 one can see that the thermal shock showed a negative effect on nonfractured core permeabilityʼs. Around 50% reduction on permeability of core 1MIS was observed as a result of thermal shock at 150°C. Thermal shock produce a shrinkage of rock which seems to result in damaging the channels that connecting the pores and responsible of core permeability. At very low permeability (0.11 Md.) this phenomena did not take place as shown in Fig.1. Therefore non-fractured core damaging due to thermal shock is function of permeability and thermal shock has no effect on very tight formation.

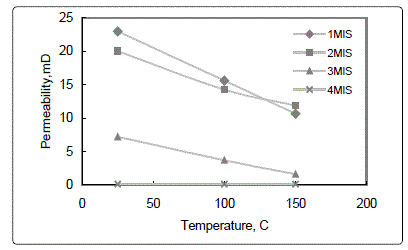
Figure 1: Effect of thermal shock on non-fractured core permeability

The second set consists of fractured core samples. Thermal shock procedures were repeated on the fractured core samples at temperatures of 150 and 200°C. Thermal shock observed to produce a positive effect on the fractured core permeability as shown in Fig. 2. The percent improvement of fractured core permeability is function of temperature. Increasing the thermal shock temperature tends to result in increasing % improvement of the thermally shocked fractured core permeability. Thermal shock tends to extend the existence fractures producing improvement in over all permeability of the fractured rock. This phenomenon was confirmed by taken micro photos of the tested rocks before and after thermal shocks. Figs. 3 and 4 show fractured rocks before and after thermal shocks of 150°C and Figs. 5 and 6 represent the thermal shock of 200°C. Fracture areas for both systems prior to and after shocks were measured using Computerized Image Analyzer. A significant increase in the fractured area after thermal was obtained, which confirms previous findings. Fig. 7 qualitatively shows σ_θ and σ_r around contraction inclusion Dusseault, in a region that is being cooled by cold-water injection in stressed porous media. Dusseault indicated that because of negative ∆V, material within the cold zone behaves “less stiff” than the surrounding media; stresses are shed to the surrounding materials. Dusseault introduced the concept of thermal contracting inclusion in a region that is being cooled by cold-water injection in a stressed porous media. He indicated that continued heat extraction due to the sudden cooling process enhances the rock fractures as shown in Fig. 7, which confirm the phenomena reported previously. All of the work conducted by Dusseault is a theoretical work.

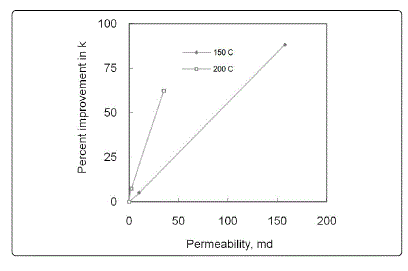
Figure 2: Effect of thermal shock on fractured cores permeability

Figure 3: Micro-photo of fractured core before thermal shock

Figure 4: Micro-photo of core sample after thermal shock, T= 150 °C.

Figure 5: Micro-photo of fractured core before thermal shock for the sample exposed to 200 C

Figure 6: Micro-photo of fractured core after thermal shock, T °C = 200

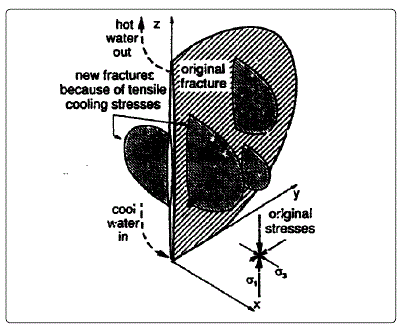
Figure 7: Geothermal fractures, large scale cooling, after Dusseault (Ref. 25).

Stress and strain of thermally shocked rocks
Non-fractured limestone rocks were used to investigate the effect of heat and thermal shocks on stress and strain of these rocks. Carbonate rocks obtained from the same outcrop having different porosity and permeability was used in this phase of the project. Initially, compression tests were performed on the selected cores prior to heating, after heating and after thermal shocks. Rocks were heated to the same temperature of 150°C. Fig. 8 shows fracture pressure versus permeability for non-heated, heated and thermally shocked systems. Thermal shock results in significant reduction of fracturing pressure for all studied systems. Expansion and contraction of the carbonate rocks as a result of heating then cooling tends to weaken the rock, which resulted in lowering its fracture pressure. The following equations were obtained from the plotted data of Fig. 8:

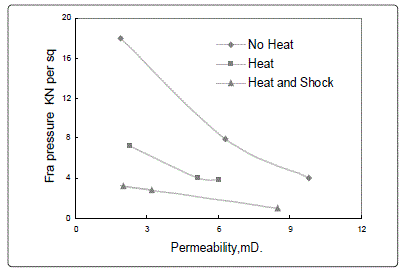
Figure 8: Permeability vs. fracture pressure for different systems

In the above, R2 values indicate near perfect correlation. The previous equations could be used to roughly estimate fracture pressure of thermally shocked limes stone strata providing availability of its permeability data. Dusseault concluded (based on theoretical work) that stress is decreases due to cold-water injection as observed experimentally in this project, as indicated in Fig. 9.

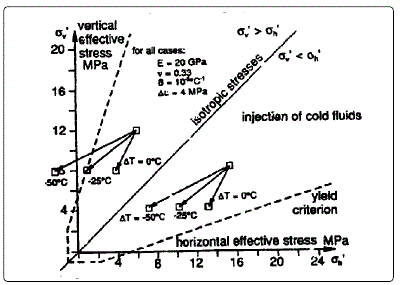
Figure 9: Stress paths for a temperature decrease, after Dusseault (Ref. 25).

Secondly, tensile tests (stress vs. strain) were performed on similar cores under different thermal (shock) stress conditions: 200, 250, and 300°C. The results of these tests is compared with a base case, no thermal shock, is shown in Fig. 10. Again the thermal shock reduced the fracture pressure of all tested samples as we compare them to the base case. Wang et al. investigated the behavior of poorly-consolidated sandstone under different loading procedures. They concluded that, for the same in situ stress, well bore hydraulic fracturing pressure might respond totally different when different stress paths have been followed. The stress history, strain path, and pore pressure distribution are critical to correctly simulate fracture propagation in poorly-consolidated sandstone.

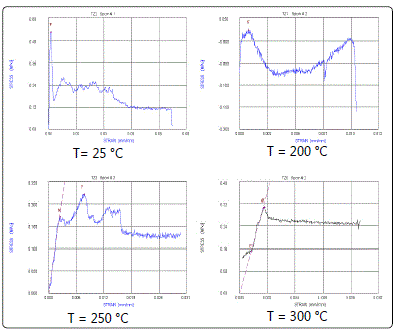
Figure 10: Stress-Strain relationship before and after thermal shocks for different temperatures

Conclusion

The following conclusions can be drawn from this study: 1. The thermal shock affects non-fractured core permeability negatively.
2. Non-fractured core damaging due to thermal shock is a function of permeability, further the thermal shock has shown no effect on very tight formations (k= 0.11).
3. Thermal shock produces a positive effect on the fractured core permeability.
4. The increase of the thermal shock temperature tends to increase the percent improvement of the thermally shocked fractured core permeability.

References

1. Timoshenko S, Woinowsky-Krieger S. Theory of Plates and Shells. 2nd Edition, McGraw-Hill, New York. 1959.
2. Boley BA, Weiner JH. Theory of Thermal Stresses. John Wiley & Sons, New York. 1960.
3. Das YC, Navaratna DR. Thermal bending of rectangular plates. J. Aerospace Sci. 1962; 29: 1397-1399.
4. Stavsky Y. Thermoelasticity of heterogeneous aeolotropic plates. ASCE J. Eng. Mech. Div. 1963; 89: 89-105.
5. Chen PYP. Transient thermal stresses in a rectangular plate due to nonuniform heat transfer coefficients. J. Thermal Stresses. 1988; 11: 115-125. doi: 10.1080/01495738808961924
6. Wu S. Analysis on transient thermal stresses in an annular fin. J. Thermal Stresses. 1997; 20: 591-615. doi: 10.1080/01495739708956120
7. Gai. X. A Coupled Geomechanics and Reservoir Flow Model on Parallel Computers. Ph.D. thesis, University of Texas at Austin, Texas, 2004.
8. Ghassemi A. A Review of Some Rock Mechanics Issues in Geothermal Reservoir Development. Geotechnical and Geological Engineering. 2012; 30(3): 647–664. doi: 10.1007/s10706-012-9508-3
9. Ghassemi A, Tarasovs S. Analysis of Fracture Propagation under Thermal Stress in Geothermal Reservoirs. Proceedings World Geothermal Congress 2015 Melbourne, Australia, 19-25 April 2015.
10. Obembe AD, Abu-Khamsin SA, Hossain ME. A Review of Modeling Thermal Displacement Processes in Porous Media. Arab J Sci Eng. 2016; 41(12): 4719–4741. doi: 10.1007/s13369-016-2265-5
11. González-Gómez WS, Alvarado-Gil JJ. Thermal effects on the physical properties of limestones from the Yucatan Peninsula. International Journal of Rock Mechanics and Mining Sciences. 2015; 75: 182-89. doi: 10.1016/j.ijrmms.2014.12.010
12. Dusseault MB, Simmons JV. Injection induced stress and fracture orientation changes. Canadian Geotech. J. 1982; 19 (4): 483-93.
13. Islam MR, Chakma A, Farouq Ali SM. State-of-the-art of in situ combustion modeling and operations. paper SPE-18755, Proc. Of the SPE California Regional Meeting, Bakersfield, CA, (April 1989.
14. Islam MR, George AE. Sand control in horizontal wells in heavy oil Reservoirs. J. Pet. Tech. 1991; 43 (7): 844-853. doi: 10.2118/18789-PA
15. Tortike WA, Farouq Ali SM. A framework for multiphase nonisothermal fluid flow in a deforming heavy oil reservoir. paper SPE 16030 presented at the Ninth SPE Symposium on Reservoir Simulation, held in San 1991. Antonio, TX, Feb. 1987.
16. Chalaturnyk R, Scot J.D. Geomechanics Issues of Steam Assisted Gravity Drainage. paper SPE 30280 presented at the International Heavy Oil Symposium held in Calgary, Alberta, Canada, 19-21 June 1995.
17. Chen HY, Teufel LW, Lee RL. Couple fluid flow and Geomechanics in reservoir study-I. Theory and governing equations.” Paper SPE 30752, paper presented at the SPE Annual Technical Conference and Exhibition, held in Dallas, USA, 1995.
18. Hojka K, Dusseault MB, Bogobowicz A. Analytical Solutions for Transient Thermoelastic Stress Fields around a Borehole during Fluid Injection into Permeable Media. Journal of Canadian Petroleum Technology. 1993; 32(4): 49-57. doi: 10.2118/93-04-03
19. Biot MA. General solutions of the equations of elasticity and consolidation for a porous material. App Phy J. 1956; 78: 91.
20. Schiffman R.L. A tehrmoelastic theory of consolidation. Environmental Geophysics and Heat Transfer. 1971; 4: 78.
21. Booker JR, Savvidou C. Consolidation around a spherical heat source. Int. J. Solids Structures. 1984; 20: 1079.
22. Kurashige MA. Thermoplastic theory of fluid-filled porous materials. Int. J. Solids Structures. 1989; 25(9): 1039-52. doi: 10.1016/0020- 7683(89)90020-6
23. Vafai K, Sozan M. Analysis of energy and momentum transport for fluid flow through a porous bed. J. Heat Transfer. 1990; 112(3): 690-99. doi: 10.1115/1.2910442
24. Chan YT, Banerjee S. Analysis of transient three-dimensional natural convection in porous media. J. Heat Transfer. 1981; 103(2): 242-48. doi: 10.1115/1.3244448
25. Dusseault MB. Stress changes in thermal operations.” Paper SPE 25809, paper presented at the SPE Int. Thermal Operations Symposium, Bakersfield, CA, and Feb. 1993.
26. Goodarzi S, Settari A, Zoback M, Keith DW. Thermal Aspects of Geomechanics and Induced Fracturing in CO₂ Injection With Application to CO₂ Sequestration in Ohio River Valley”. SPE International Conference on CO₂ Capture, Storage, and Utilization, New Orleans, Louisiana, USA. 2010.