Research Article
Approximate Analytical Expressions of Non-Linear Boundary Value problem for a Boundary Layer Flow using the Homotopy Analysis Method
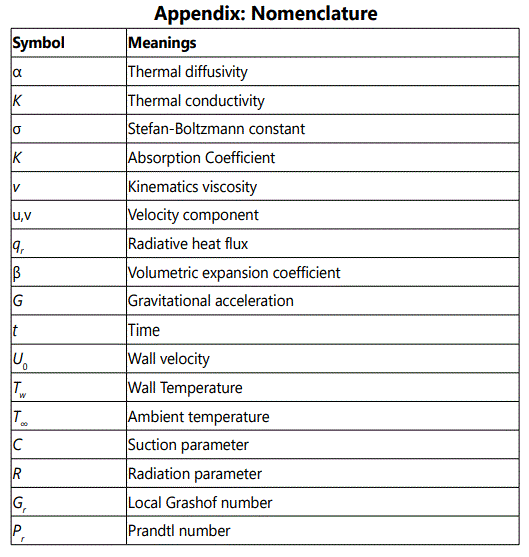
1Department of Mathematics, The Madura College, Madurai, Tamil Nadu, India
2Department of Mathematics, MSNPM Womenʼs College, Tamil Nadu, India
3M. Phil., Scholar, The Madura College, Madurai, Tamil Nadu, India
*Corresponding author: V Ananthaswamy, Assistant Professor, Department of Mathematics, The Madura College, Madurai, Tamil Nadu, India, E-mail: ananthu9777@rediffmail.com
Received: April 5, 2019 Accepted: April 24, 2019 Published: May 2, 2019
Citation: Ananthaswamy V, Subha M, Mohamed Fathima A. Approximate Analytical Expressions of Non-Linear Boundary Value problem for a Boundary Layer Flow using the Homotopy Analysis Method. Madridge J Bioinform Syst Biol. 2019; 1(2): 34-39. doi: 10.18689/mjbsb-1000107
Copyright: © 2019 The Author(s). This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, we discuss the analytical expressions of velocity and heat transfer for a boundary layer flow with thermal radiation past a moving vertical porous plate. The governing non-linear differential equations are solved analytically using Homotopy analysis method. The results are presented as velocity, temperature, local wall shear stress and wall heat transfer rate profiles various values of parameter involving in the problem. Our analytical results are compared with the previous work and a good agreed is observed.
Keywords: Thermal Radiation; Porous Plate; Non-Linear Boundary Value Problem; Local Wall Shear Stress; Wall Heat Transfer Rate; Homotopy Analysis Method.
Introduction
The study of the flow and heat transfer in fluid past a porous surface has many interesting applications in the field of engineering, especially in physical and chemical industries [1-6]. Makinde et al. [1] investigated the Adomian decomposition approach to a boundary layer flow with thermal radiation past a moving vertical porous plate. Adomian [3] examined a review of the decomposition method in applied mathematics. Adomian et al. [4] investigated the solution of nonlinear ordinary and partial differential equations of physics. Chung et al. [7] examined the stability of steady flow in a channel with linear temperature dependent viscosity. Hayat et al. [8] investigated the hydromagnetic oscillatory flow of a fluid bounded by a porous plate when the entire system rotates about axis normal to the plate.
Hassanien [9] examined the heat transfer in a power law fluid over a non-isothermal stretching sheet. Howell et al. [10] investigated momentum and heat transfer on a continuously moving surface in a power law fluid. Ibrahim et al. [11] examined the method of similarity reduction for problems of radiative and magnetic field effect on free convection and mass transfer flow past a semi-infinite flat plate. Makinde [12] examined free convection flow with thermal radiation and mass transfer past a moving vertical porous plate. Sivasankaran et al. [13] investigated the natural convection heat and mass transfer fluid past an inclined semi-infinite porous surface. Terrill [14] examined slow laminar flow in a converging or diverging channel with suction at one wall and blowing at the other wall. Uzan [15] investigated the heat transfer to a power law fluid in arbitrary cross sectional ducts. Yu-shu et al. [16] examined a numerical for simulating non-Newtonian fluid flow and displacement in porous media. Badr et al [5] investigated the numerical simulation of steady and unsteady mixed convection from tubes of elliptic cross-section. The study revealed that the effect of fluctuations on the time-average Nusselt number becomes more pronounced with increasing Reynolds number. It also revealed that the rate of heat transfer increases with the increase of the amplitude of fluctuations but decreases with the increase of frequency. Yurusoy et al. [17] examined the exact solution of boundary layer equations of a non-Newtonian fluid over a stretching sheet by the method of lie group analysis. This paper demonstrates the solution of the velocity and heat transfer in a boundary layer flow with thermal radiation past a moving vertical porous plate using Homotopy analysis method and discussed by graphically.
Mathematical Formulation of the Problem
Consider an unsteady flow of an incompressible fluid with thermal radiation past a moving vertical plate. Let the x-axis be taken along the plate in the vertically upwards direction and the y-axis be taken normal to it. Let u and v be the velocity components along the x and y respectively. The physical variables are functions of y and t only. Hence, the governing equations are as follows:

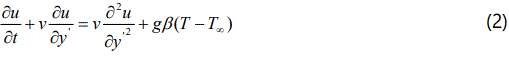

The radiative heat flux term is simplified by making use of the Roseland approximation as in eqn (1).

Where, α denote thermal diffusivity, k is thermal conductivity, σ denote Stefan–Boltzmann constant, K is absorption Coefficient, v is Kinematics viscosity, u,v denote velocity component, qr is Radiative heat flux, β is Volumetric expansion coefficient(Temperature), G denote Gravitational acceleration, t is Time, U0 denote wall velocity, Tw is Wall Temperature, T∞ denote ambient temperature, c is suction parameter, R is radiation parameter, Gr denote local Grash of number, Pr is Prandtl number.
The appropriate boundary conditions are

We can define the similarity variables are as follows:

Here the length scale is defined as
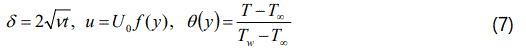
Taking the Taylor series expansion of T4 and neglecting terms with higher powers, we have

Using the eqns. (7) and (8) into the eqns. (2) to (4) we obtained the non-linear ordinary differential equations are as follows:


The corresponding boundary conditions are as follows:
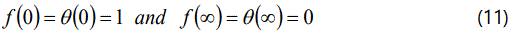
Here
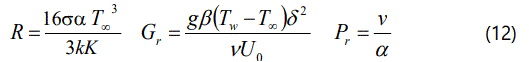
The local wall shear stress (Skin friction) can be defined as
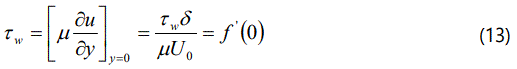
The Local surface heat flux
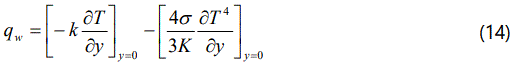
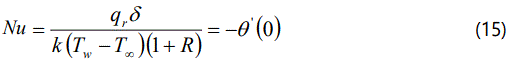
Solution of the Non-Linear Boundary problem using the Homotopy Analysis Method
This section deals with a basic strong analytic tool for non-linear problems, namely the Homotopy analysis method (HAM) which was generated by Liao [18], is employed to solve the nonlinear differential eqns. (9)–(11). The Homotopy analysis method is based on a basic concept in topology. Unlike perturbation techniques like [19], the Homotopy analysis method is independent of the small/large parameters. Unlike all other reported perturbation and non-perturbation techniques such as the artificial small parameter method [20], the δ-expansion method [21] and Adomianʼs decomposition method [22], the Homotopy analysis method provides us a simple way to adjust and control the convergence region and rate of approximation series. The Homotopy analysis method has been successfully applied to many nonlinear problems such as heat transfer [23], viscous flows [24], nonlinear oscillations [25], Thomas-Fermiʼs atom model [26], nonlinear water waves [27], etc. Such varied successful applications of the Homotopy analysis method confirm its validity for nonlinear problems in science and engineering. The Homotopy analysis method is a good technique when compared to other perturbation methods. The existence of the auxiliary parameter h in the Homotopy analysis method provides us with a simple way to adjust and control the convergence region of the solution series.
Basic concepts of the Homotopy analysis method [18-29]
Consider the following differential equation:

Where N is a nonlinear operator, t denotes an independent variable, u(t) is an unknown function. For simplicity, we ignore all boundary or initial conditions, which can be treated in the similar way. By means of generalizing the conventional Homotopy method, Liao constructed the so-called zero-order deformation equation as:
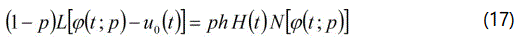
Where p ∈ [0,1] is the embedding parameter, h≠0 is a nonzero auxiliary parameter, H(t) ≠ 0 is an auxiliary function, L an auxiliary linear operator, u0(t) is an initial guess of u(t), φ (t; p) is an unknown function. It is important to note that one has great freedom to choose auxiliary unknowns in HAM. Obviously, when p=0 and p=1, it holds:
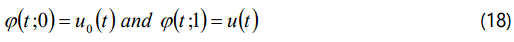
respectively. Thus, as P increases from 0 to 1, the solution φ (t; p) varies from the initial guess u0(t) to the solution u (t).
Expanding φ (t; p) in Taylor series with respect to p, we have:


If the auxiliary linear operator, the initial guess, the auxiliary parameter h, and the auxiliary function are so properly chosen, the series eqn.(18) converges at p=1 then we have:

Differentiating the eqn. (16) for m times with respect to the embedding parameter p, and then setting p=0 and finally dividing them by m!, we will have so-called m th order deformation equation as:
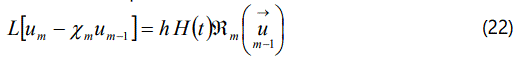
Where
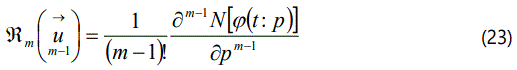
and

Applying L-1 on both side of eqn.(22), we get
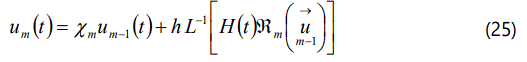
In this way, it is easily to obtain um for m ≥ 1, at Mth order, we have

when M→ +∞, we get an accurate approximation of the original eqn.(16). For the convergence of the above method we refer the reader to Liao [19]. If an eqn. (16) admits unique solution, then this method will produce the unique solution.
Approximate analytical expressions of the non-linear differential eqns. (9) and (10) using Homotopy analysis method
In this section, we find the analytical expressions for the eqns. (9) and (10) with the help of the eqn.(10). We construct Homotopy for the eqns.(9) and (10) are as follows:
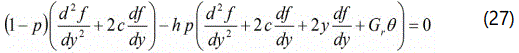
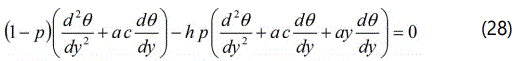
The approximate solution of the eqns.(27) and (28) are as follows:
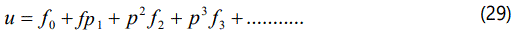
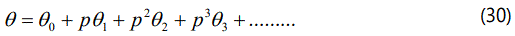
The initial approximations are as follows:



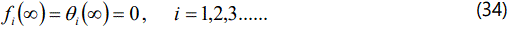
Substituting the eqns. (29) and (30) into the eqns. (27) and (28) respectively we get
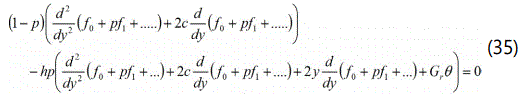
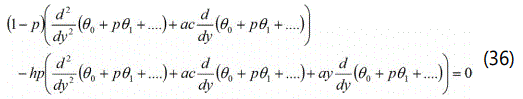
Comparing the coefficients of p0, p1 in the eqns.(35) and (36) we get

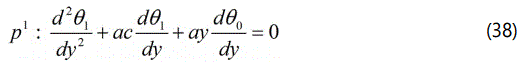

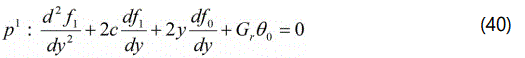
Solving the eqns. (37)-(40) with the help of the eqns. (31)-(34) we get the following results:


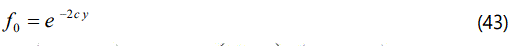
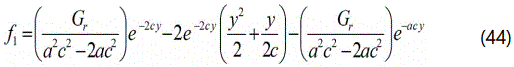
Where

According to the HAM, we can conclude that


Substituting the eqns. (43) and (44) into an eqn. (46) and using the eqns. (41) and (42) into an eqn. (47) we get the following:
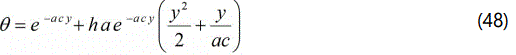
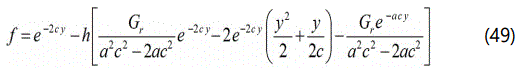
The analytical expression of the dimensionless skin friction using the eqn. (13) is given by Skin friction
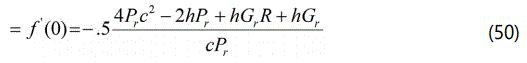
The analytical expression of the Wall heat transfer rate using the eqn. (15) is given by
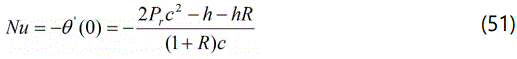
Results and Discussion
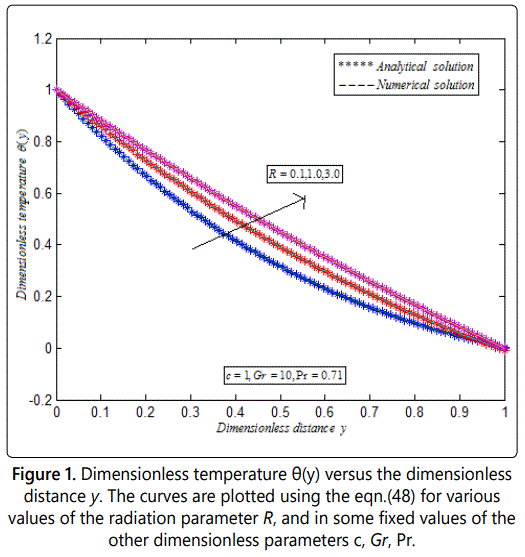
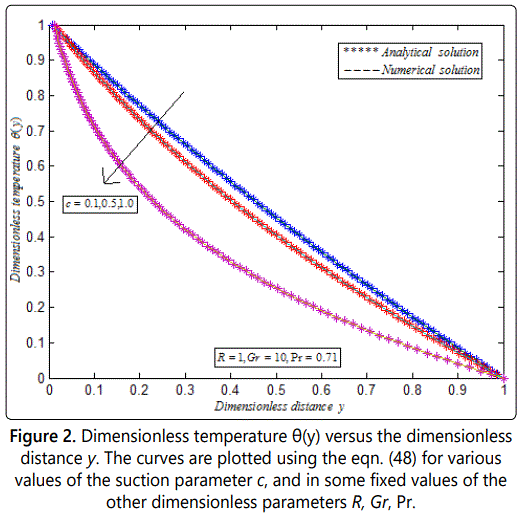
Figures 1 and 2 represents dimensionless temperature θ(y) versus dimensionless distance y. From figure 1, it is noted that the temperature increases when the radiation parameter R increases, and in some fixed values of the other dimensionless parameters. From figure 3, it is inferred that when the suction parameter c increases the corresponding temperature decreases in some fixed values of the other parameters.
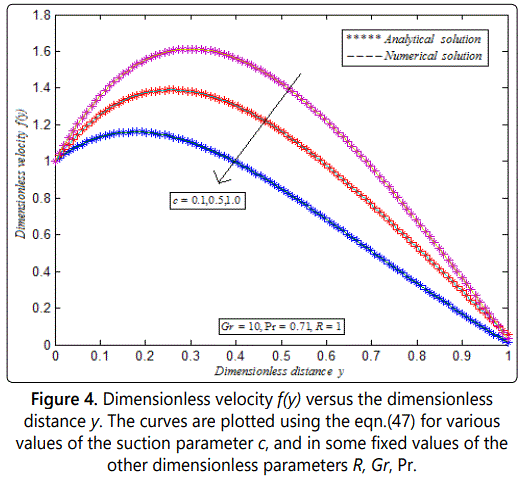
Figures 3 and 4 represent dimensionless velocity f(y) versus dimensionless distance y. From figure 3, it is noted that the velocity increases when the radiation parameter R increases, and in some fixed values of the other dimensionless parameters. From figure 4, it is inferred that when the suction parameter c increases the corresponding velocity decreases in some fixed values of the other parameters.
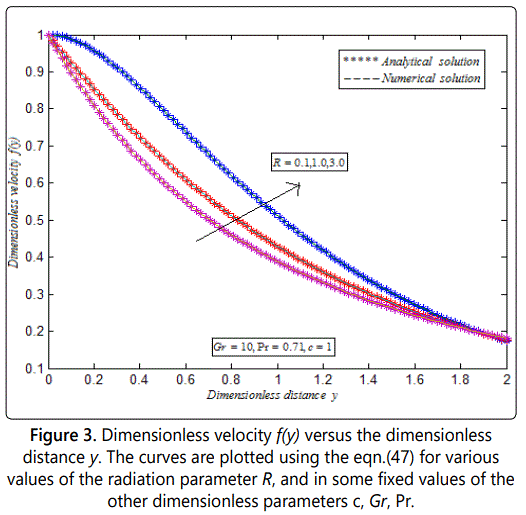
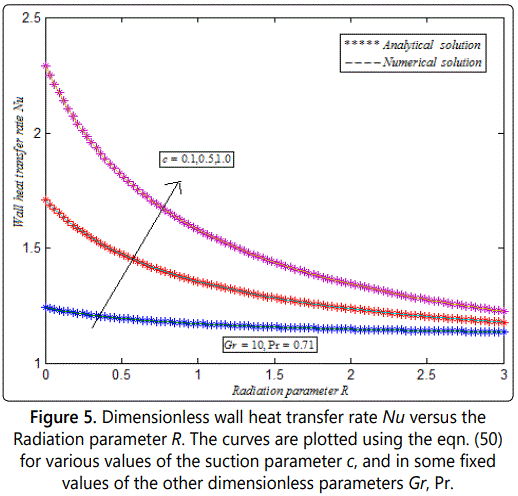
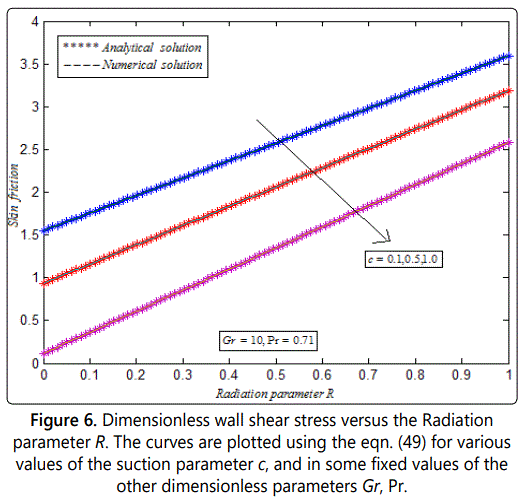
Figure 5 represents wall heat transfer rate Nu versus radiation parameter R. From figure 5, it is observed that the wall heat transfer rate increases when the suction parameter increases, and in some fixed values of the other dimensionless parameters. Figure 6 represents wall shear stress versus radiation parameter R. From figure 6, it is inferred that the wall shear stress decreases when the suction parameter increases, and in some fixed values of the other dimensionless parameters.
Conclusion
In this paper the Homotopy analysis method is employed to mathematical study of a boundary layer flow with thermal radiation past a moving vertical porous plate. The approximate analytical expressions of the velocity and temperature profiles are derived mathematically and graphically using the Homotopy analysis method. The approximate analytical expressions of the wall shear stress and wall heat transfer rate are also derived using the analytical expressions for the velocity and temperature profiles. We also discussed the graphical representations of the wall shear stress and the wall heat transfer rate. The Homotopy analysis method can be easily extended to solve the other non-linear boundary value problems in physical and chemical sciences.
References
- Makinde OD, Olajuwon BI, Gbolagade AW. Adomian decomposition approach to a boundary layer flow with thermal radiation past a moving vertical porous plate. International Journal of Applied Mathematics and Mechanics. 2007; 3(3): 62-70.
- Adomian G. Solving Frontier Problems of Physics: The Decomposition Method. Boston. MA: Kluwer 1994.
- Adomian G. A review of the decomposition method in applied mathematics. J Math Anal Appl. 1988; 135(2): 501-504. doi: 10.1016/0022-247X(88)90170-9
- Badr HM, Ahmed EH. Numerical simulation of steady and unsteady mixed. Convection from tubes of elliptic cross-section. Proceedings of the third International Conference on Engineering Computational Technology. 2002; 135: 73-74.
- Adomian G, Rach R. Solution of nonlinear ordinary and partial differential equations of physics. Journal of Mathematical and Physical Sciences. 1991; 25: 703-718.
- Bird RB, Stewart WE, Light Foot EN. Transport phenomena. John Wiley and Sons, Inc. New York, USA. 1960.
- Chung BJ, Vaidya A, Wulandana R. Stability of steady flow in a channel in a channel with linear temperature dependent viscosity. International Journal of Applied Mathematics and Mechanics. 2006; 2(1): 24-33.
- Hayat T, Hutter K, Nadeem S, Asghar S. Unsteady Hydromagnetic rotating flow of a conducting second grade fluid. Z Angew Math Phys. 2004; 55(4): 626-641.
- Hassanien IA, Abdullah AA, Gorla RSR. Flow and heat transfer in a power law fluid over a non-isothermal stretching sheet. Math Comput Model. 1998; 28(9): 105-116.
- Howell TG, Jeng DR, De Witt KJ. Momentum and heat transfer on a continuous moving surface in a power law fluid. Int J Heat Mass Transf. 1997; 40: 1853-1861. doi: 10.1016/S0017-9310(96)00247-5
- Ibrahim FS, Mansour MA, Hamad MAA. Lie-group analysis of radiative and magnetic field effects on free convection and mass transfer flow past a semi-infinite vertical flat plate. Electronic Journal of Differential Equation. 2005; 39: 1-17.
- Makinde OD. Free convection flow with thermal radiation and mass transfer past a moving vertical porous plate. Int J Heat Mass Transf. 2005; 32: 1411-1419. doi: 10.1016/j.icheatmasstransfer.2005.07.005
- Sivasankaran S, Bhuvaneswari M, Kandaswamy P, Ramasami EK. Lie group analysis of natural convection heat and mass transfer in an inclined porous surface with heat generation. International Journal of Applied Mathematics and Mechanics. 2006; 2(2): 34-40.
- Terrill RM. Slow laminar flow in a converging or diverging channel with suction at one wall and blowing at the other wall. Z Angew Math Phys. 1965; 16(2): 306-308.
- Uzun I. Heat transfer to a power law fluid in arbitrary cross sectional ducts. Turkish J Eng Env Sci. 2002; 26(2): 7-14.
- Yu-shu Wu, Karsten P. A numerical for simulating non-Newtonian fluid flow and displacement in porous media. Adv Water Resour. 1998; 21(5): 351-362.
- Yurusoy M, Pakdemirli M. Exact solutions of boundary layer equations of a special non-Newtonian fluid over a stretching sheet. Mech Res Commun. 1999; 26(2): 171-175.
- Liao SJ, Cheung KF. Homotopy analysis of nonlinear progressive waves in deep water. J Eng Math. 2003; 45(2): 105-116.
- Kierkus WT. An analysis of laminar free convection flow and heat transfer about an inclined isothermal plate. Int J Heat Mass Transf. 1968; 11: 241-253. doi: 10.1016/0017-9310(68)90153-1
- Liao SJ. An explicit totally analytic approximation of Blasius viscous flow problems. Int J Non Linear Mech. 1999; 34: 759-778. doi: 10.1016/S0020-7462(98)00056-0
- Liao SJ, Chwang AT. Application of homotopy analysis method in nonlinear oscillations. J Appl Mech. 1998; 65: 914-922. doi: 10.1115/1.2791935
- Liao SJ. An analytical approximate technique for free oscillations of positively damped systems with algebraically decaying amplitude. Int J Non Linear Mech. 2003; 38(8): 1173-1183. doi: 10.1016/S0020-7462(02)00062-8
- Liao SJ. An analytic approximation of the drag coefficient for the viscous flow past a sphere. Int J Non Linear Mech. 2002; 37(1): 1-18. doi: 10.1016/S0020-7462(00)00092-5
- Liao SJ. The Homotopy Analysis method in non-linear differential equations. Springer and Higher Education Press. 2012: 45-54.
- Ananthaswamy V, Uma Maheswari S. Analytical expression for the hydrodynamic fluid flow through a porous medium. International Journal of Automation and Control Engineering. 2015; 4(2): 67-76.
- Ananthaswamy V, Iswarya T. Analytical expressions of mass transfer effects on unsteady flow past an accelerated vertical porous plate with suction. Nonlinear Studies. 2016; 23(1): 73-86.
- Ananthaswamy V, Iswarya T. Analytical expressions of the effect of radiation on free convection flow of heat and mass transfer. Nonlinear Studies. 2016; 23(1): 133-147.